Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-15T01:54:13.589Z Has data issue: false hasContentIssue false
  • English
  • Français

On a denumerable partition problem of Erdős

Published online by Cambridge University Press:  24 October 2008

Roy O. Davies
Roy O. Davies
Affiliation:
Leicester University
Get access Rights & Permissions [Opens in a new window]

Extract

Solving a problem of Erdős(5), I recently proved (4) that for n = 1, 2, …, the hypothesis 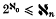implies that if the lines in the Euclidean space Ek (k ≥ 2) are distributed into n + 2 disjoint classes Li(i = 1, …,n + 2), then there exists a decomposition of Ek into 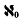sets Si such that the intersection of each line of Li with the corresponding set Si is finite. Without assuming any hypothesis other than the axiom of choice, I have also recently proved (3) that if di (i = 1,2,…) is any infinite sequence of mutually non-parallel lines in the plane, then the plane can be decomposed into N0 sets Si such that each line parallel to di intersects the corresponding set 8i in at most a single point.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 501 - 502
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bagemihi, F., A proposition of elementary plane geometry that implies the continuum hypothesis. Z. Math. Logik Grundlagen Math. 7 (1961), 77–79.CrossRefGoogle Scholar
(2)Davies, ROY O., The power of the continuum and some propositions of plane geometry. Fund. Math. (in the press).Google Scholar
(3)Davies, ROY O., Covering the plane with denumerably many curves. J. London Math. Soc. (in the press).Google Scholar
(4)Davies, ROY O., On a problem of Erőds concerning decompositions of the plane. Proc. Cambridge Philos. Soc. 59 (1963), 33–36.Google Scholar
(5)ErdőS, P., Some remarks on set theory IV. Michigan Math. J. 2 (1953–1954), 169–173.Google Scholar