Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hurley, D. G.
1989.
Mathematical research at the Aeronautical Research Laboratories 1939–1960.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 30,
Issue. 4,
p.
389.


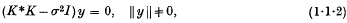
 ,
, 