Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Belshoff, Richard
Slattery, Susan
and
Wickham, Cameron
1996.
The local cohomology modules of Matlis reflexive modules are almost cofinite.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 9,
p.
2649.
Kawasaki, Ken-ichiroh
1996.
On the finiteness of Bass numbers of local cohomology modules.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 11,
p.
3275.
Yoshida, Ken-Ichi
1997.
Cofiniteness of local cohomology modules for ideals of dimension one.
Nagoya Mathematical Journal,
Vol. 147,
Issue. ,
p.
179.
Yassemi, Siamak
2001.
COFINITE MODULES.
Communications in Algebra,
Vol. 29,
Issue. 6,
p.
2333.
Khashyarmanesh, K.
and
Salarian, Sh.
2002.
A FINITENESS RESULT FOR LOCAL COHOMOLOGY MODULES.
Communications in Algebra,
Vol. 30,
Issue. 10,
p.
4821.
Asadollahi, J.
Khashyarmanesh, K.
and
Salarian, SH.
2003.
A generalization of the cofiniteness problem in local cohomology modules.
Journal of the Australian Mathematical Society,
Vol. 75,
Issue. 3,
p.
313.
Melkersson, Leif
2005.
Modules cofinite with respect to an ideal.
Journal of Algebra,
Vol. 285,
Issue. 2,
p.
649.
Khashyarmanesh, Kazem
2006.
On the finiteness properties of extension and torsion functors of local cohomology modules.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 5,
p.
1319.
Khashyarmanesh, K.
and
Khosh-Ahang, F.
2008.
On the Local Cohomology of Matlis Reflexive Modules.
Communications in Algebra,
Vol. 36,
Issue. 2,
p.
665.
Sabzrou, Hossein
and
Tousi, Massoud
2008.
Local Cohomology at Monomial Ideals inR-Sequences.
Communications in Algebra,
Vol. 36,
Issue. 1,
p.
37.
Kawasaki, Ken-ichiroh
2008.
On finiteness properties of local cohomology modules over Cohen–Macaulay local rings.
Illinois Journal of Mathematics,
Vol. 52,
Issue. 3,
Bahmanpour, Kamal
and
Naghipour, Reza
2009.
Cofiniteness of local cohomology modules for ideals of small dimension.
Journal of Algebra,
Vol. 321,
Issue. 7,
p.
1997.
Mafi, Amir
2009.
A generalization of the finiteness problem in local cohomology modules.
Proceedings - Mathematical Sciences,
Vol. 119,
Issue. 2,
p.
159.
Mafi, Amir
2009.
Matlis reflexive and generalized local cohomology modules.
Czechoslovak Mathematical Journal,
Vol. 59,
Issue. 4,
p.
1095.
Khashyarmanesh, Kazem
2009.
A Characterization of Gorenstein Rings and Grothendieck's Conjecture.
Algebra Colloquium,
Vol. 16,
Issue. 04,
p.
653.
Abazari, Rasoul
and
Bahmanpour, Kamal
2011.
Cofiniteness of extension functors of cofinite modules.
Journal of Algebra,
Vol. 330,
Issue. 1,
p.
507.
Kawasaki, Ken-ichiroh
2011.
On a category of cofinite modules which is Abelian.
Mathematische Zeitschrift,
Vol. 269,
Issue. 1-2,
p.
587.
Khashyarmanesh, Kazem
Koşan, M. Tamer
and
Şahinkaya, Serap
2012.
On Weakly Laskerian and Weakly Cofinite Modules.
Algebra Colloquium,
Vol. 19,
Issue. 04,
p.
693.
Sadeghi, Behrouz
Bahmanpour, Kamal
and
A’zami, Jafar
2013.
Artinian cofinite modules over complete Noetherian local rings.
Czechoslovak Mathematical Journal,
Vol. 63,
Issue. 4,
p.
877.
Irani, Yavar
and
Bahmanpour, Kamal
2013.
FINITENESS PROPERTIES OF EXTENSION FUNCTORS OF COFINITE MODULES.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 2,
p.
649.


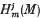 are artinian,
are artinian, 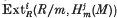 is finitely generated for all
is finitely generated for all