Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Longuet-Higgins, M. S.
1960.
Mass transport in the boundary layer at a free oscillating surface.
Journal of Fluid Mechanics,
Vol. 8,
Issue. 2,
p.
293.
1975.
Integral properties of periodic gravity waves of finite amplitude.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 342,
Issue. 1629,
p.
157.
1976.
The deformation of steep surface waves on water - I. A numerical method of computation.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 350,
Issue. 1660,
p.
1.
Lim, T. H.
and
Smith, A. C.
1978.
A Cauchy integral-equation method for the numerical solution of the steady water-wave problem.
Journal of Engineering Mathematics,
Vol. 12,
Issue. 4,
p.
325.
Meyer, R.E.
1979.
Vol. 19,
Issue. ,
p.
53.
Longuet-Higgins, M. S.
1980.
Spin and angular momentum in gravity waves.
Journal of Fluid Mechanics,
Vol. 97,
Issue. 01,
p.
1.
Hwung, H. H.
and
Tsai, C. P.
1982.
On the Variation of Characteristics of Two Wave Trains Crossing in Intermediate Depth.
p.
862.
Constantin, A.
2016.
Extrema of the dynamic pressure in an irrotational regular wave train.
Physics of Fluids,
Vol. 28,
Issue. 11,
Umeyama, Motohiko
2019.
Theoretical Considerations, Flow Visualization and Pressure Measurements for Rear-End Collisions of Two Unequal Solitary Waves.
Journal of Mathematical Fluid Mechanics,
Vol. 21,
Issue. 1,
Aleman, A.
and
Constantin, A.
2020.
On the decrease of kinetic energy with depth in wave–current interactions.
Mathematische Annalen,
Vol. 378,
Issue. 3-4,
p.
853.
Roberti, Luigi
2020.
On the decrease of velocity with depth in irrotational periodic water waves.
Monatshefte für Mathematik,
Vol. 193,
Issue. 3,
p.
671.
Henry, David
2021.
On the energy of nonlinear water waves.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 477,
Issue. 2255,
Klahn, Mathias
Madsen, Per A.
and
Fuhrman, David R.
2021.
Simulation of three‐dimensional nonlinear water waves using a pseudospectral volumetric method with an artificial boundary condition.
International Journal for Numerical Methods in Fluids,
Vol. 93,
Issue. 6,
p.
1843.
Constantin, Olivia
2022.
A complex-analytic approach to kinetic energy properties of irrotational traveling water waves.
Mathematische Zeitschrift,
Vol. 301,
Issue. 4,
p.
4201.
Henry, David
2022.
Energy considerations for nonlinear equatorial water waves.
Communications on Pure and Applied Analysis,
Vol. 21,
Issue. 7,
p.
2337.
Constantin, O.
and
Persson, A.-M.
2022.
A complex-analytic approach to kinetic energy properties of irrotational flows.
Proceedings of the American Mathematical Society,
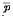 increase with z.
increase with z.

