Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T05:02:16.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Permutable quasiregular maps

Part of: Complex dynamical systems Entire and meromorphic functions, and related topics Geometric function theory

Published online by Cambridge University Press:  03 June 2021

ATHANASIOS TSANTARIS
ATHANASIOS TSANTARIS*
Affiliation:
School of Mathematical Sciences, University of Nottingham, NottinghamNG7 2RD. e-mail: Athanasios.Tsantaris@nottingham.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f and g be two quasiregular maps in 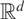$\mathbb{R}^d$ that are of transcendental type and also satisfy 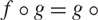$f\circ g =g \circ f$ . We show that if the fast escaping sets of those functions are contained in their respective Julia sets then those two functions must have the same Julia set. We also obtain the same conclusion about commuting quasimeromorphic functions with infinite backward orbit of infinity. Furthermore we show that permutable quasiregular functions of the form f and 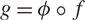$g = \phi \circ f$ , where 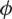$\phi$ is a quasiconformal map, have the same Julia sets and that polynomial type quasiregular maps cannot commute with transcendental type ones unless their degree is less than or equal to their dilatation.

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions 30C65: Quasiconformal mappings in $^n$, other generalizations
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 1 , July 2022 , pp. 105 - 121
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

References

Baker, I. N.. Zusammensetzungen ganzer funktionen. Math. Z. 69 (1958), 121–163.CrossRefGoogle Scholar
Baker, I. N.. Permutable entire functions. Math. Z. 79 (1962), 243–249.CrossRefGoogle Scholar
Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc 49 (1984), 563–576.CrossRefGoogle Scholar
Benini, A. M., Rippon, P. J. and Stallard, G. M.. Permutable entire functions and multiply connected wandering domains. Adv. Math. 287 (2016), 451–462.CrossRefGoogle Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151–188.CrossRefGoogle Scholar
Bergweiler, W.. Fixed points of composite entire and quasiregular maps. Ann. Acad. Sci. Fenn. Math. 31 (2006), 523–540.Google Scholar
Bergweiler, W.. Iteration of quasiregular mappings. Comput. Meth. Function Theory 10 (2010), 455–481.CrossRefGoogle Scholar
Bergweiler, W.. Fatou–Julia theory for non-uniformly quasiregular maps. Ergodic Theory Dynam. Systems 33 (2013), no. 1, 1–23.Google Scholar
Bergweiler, W. and Hinkkanen, A.. On semiconjugation of entire functions. Math. Proc. Camb. Phil. Soc. 137 (1999), 641–651.CrossRefGoogle Scholar
Bergweiler, W., Drasin, D. and Fletcher, A.. The fast escaping set for quasiregular mappings. Anal. Math. Phys. 4 (2014), 83–98.CrossRefGoogle Scholar
Bergweiler, W., Fletcher, A., Langley, J. and Meyer, J.. The escaping set of a quasiregular mapping. Proc. Amer. Math. Soc. 137 (2009), no. 2, 641–651.CrossRefGoogle Scholar
Bergweiler, W., Fletcher, A. and Nicks, D.. The Julia set and the fast escaping set of a quasiregular mapping. Comput. Methods Funct. Theory 14 (2014), 209–218.CrossRefGoogle Scholar
Bergweiler, W. and Nicks, D. A.. Foundations for an iteration theory of entire quasiregular maps. Israel J. Math 201 (2014), no. 1, 147–184.CrossRefGoogle Scholar
Carleson, L. and Gamelin, T. W.. Complex dynamics. Universitext (Springer-Verlag, New York, 1993).CrossRefGoogle Scholar
Eremenko, A. E.. On some functional equations connected with iteration of rational functions. Leningrad Math J. 1 (1990), no. 4, 905–919.Google Scholar
Fatou, P.. Sur les equations fonctionelles. Bull. Soc. Math. France 47-48 (1919, 1920), 161–271, 33–94, 208–314.CrossRefGoogle Scholar
Fatou, P.. Sur l’iteration analytique et les substitutions permutables. J. Math. Pures Appl. 2 (1923), 343–384.Google Scholar
Fatou, P.. Sur l’iteration des fonctions transcendantes entieres. Acta Math. 47 (1926), 337–370.CrossRefGoogle Scholar
Fletcher, A. N. and Nicks, D. A.. Quasiregular dynamics on the n-sphere. Ergodic Theory Dynam. Systems 31 (2010), no. 1, 23–31.Google Scholar
Ganapathy Iyer, V.. On permutable integral functions. J. London Math. Soc. s1-34 (1959), no. 2, 141–144.CrossRefGoogle Scholar
Julia, G.. Sur l’iteration des fonctions rationelles. J. Math. Pures Appl. 4 (1918), no. 7, 47–245.Google Scholar
Julia, G.. Memoire sur la permutabilite des fractions rationnelles. Ann. Sci. École Norm. Sup. 39 (1922), no. 3, 131–215.CrossRefGoogle Scholar
Littlewood, J. E. and Offord, A. C.. On the distribution of zeros and α-values of a random integral function. Ann. of Math. 49 (1948), 885–952.CrossRefGoogle Scholar
Mayer, V.. Uniformly quasiregular mapings of Lattes type. Conform. Geom. Dyn. 1 (1997), 104–111.CrossRefGoogle Scholar
Mayer, V.. Quasiregular analogs of critically finite rational functions with parabolic orbifold. J. D’Analyse Mathematique 75 (1998), 105–119.CrossRefGoogle Scholar
Milnor, J.. On Lattès maps. arXiv:math/0402147 (2004).Google Scholar
Milnor, J.. Dynamics in one complex variable. Ann. of Math. Stud. (Princeton University Press, 2006).Google Scholar
Nicks, D. A. and Sixsmith, D. J.. Periodic domains of quasiregular maps. Ergodic Theory Dynam. Systems 38 (2018), 2321–2344.CrossRefGoogle Scholar
Nicks, D. and Sixmith, D.. Hollow quasi-fatou components of quasiregular maps. Math. Proc. Cambridge Phil. Soc. 162 (2017), no. 3, 561–574.CrossRefGoogle Scholar
Osborne, J. W. and Sixsmith, D. J.. On permutable meromorphic functions. Aequationes Math. 90 (2016), no. 5, 1025–1034.CrossRefGoogle Scholar
Pólya, G.. On an integral function of an integral function. J. London Math. Soc. s1-1 (1926), no. 1, 12–15.CrossRefGoogle Scholar
Rickman, S.. On the number of omitted values of entire quasiregular mappings. J. d’Analyse Mathématique 37 (1980), 100–117.CrossRefGoogle Scholar
Rickman, S.. The analogue of Picard’s theorem for quasiregular mappings in dimension three. Acta Math. 154 (1985), 195–242.CrossRefGoogle Scholar
Rickman, S.. Quasiregular mappings, vol. 26. Ergeb. Math. Grenzgeb., no. 3 (Springer-Verlag, Berlin, 1993).Google Scholar
Rippon, P. J. and Stallard, G. M.. On questions of Fatou and Eremenko. Proc. Amer. Math. Soc. 133 (2005), 1119–1126.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. Fast escaping points of entire fucntions. Proc. London Math. Soc. 105 (2012), no. 4, 787–820.CrossRefGoogle Scholar
Ritt, J. F.. On the iteration of rational functions. Trans. Amer. Math. Soc. 21 (1920), no. 3, 348–356.CrossRefGoogle Scholar
Ritt, J. F.. Permutable rational functions, Trans. Amer. Math. Soc. 25 (1923), no. 3, 291–309.CrossRefGoogle Scholar
Vuorinen, M.. Conformal geometry and quasiregular mappings. Lecture Notes in Math., vol. 1319 (Springer–Verlag, Berlin, 1988).Google Scholar
Warren, L.. On the iteration of quasimeromorphic mappings, Math. Proc. Camb. Phil. Soc. 168 (2018), no. 1, 1–11, Advance online publication. doi: 10.1017/s030500411800052x.CrossRefGoogle Scholar
Warren, L.. Constructing a quasiregular analogue of z exp(z) in dimension 3. arXiv:1907.04720.Google Scholar
Zorich, V. A.. The theorem of M. A. Lavrent’ev on quasiconformal mappings in space. Mat. Sb. 74 (1967), 417–433.Google Scholar