No CrossRef data available.
Article contents
Quasiconformality and hyperbolic skew
Published online by Cambridge University Press: 18 December 2020
Abstract
We prove that if 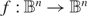 $f:\mathbb{B}^n \to \mathbb{B}^n$
, for n ≥ 2, is a homeomorphism with bounded skew over all equilateral hyperbolic triangles, then f is in fact quasiconformal. Conversely, we show that if
$f:\mathbb{B}^n \to \mathbb{B}^n$
, for n ≥ 2, is a homeomorphism with bounded skew over all equilateral hyperbolic triangles, then f is in fact quasiconformal. Conversely, we show that if 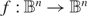 $f:\mathbb{B}^n \to \mathbb{B}^n$
is quasiconformal then f is η-quasisymmetric in the hyperbolic metric, where η depends only on n and K. We obtain the same result for hyperbolic n-manifolds. Analogous results in
$f:\mathbb{B}^n \to \mathbb{B}^n$
is quasiconformal then f is η-quasisymmetric in the hyperbolic metric, where η depends only on n and K. We obtain the same result for hyperbolic n-manifolds. Analogous results in 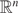 $\mathbb{R}^n$
, and metric spaces that behave like
$\mathbb{R}^n$
, and metric spaces that behave like 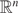 $\mathbb{R}^n$
, are known, but as far as we are aware, these are the first such results in the hyperbolic setting, which is the natural metric to use on
$\mathbb{R}^n$
, are known, but as far as we are aware, these are the first such results in the hyperbolic setting, which is the natural metric to use on 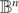 $\mathbb{B}^n$
.
$\mathbb{B}^n$
.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 3 , November 2021 , pp. 449 - 466
- Copyright
- © Cambridge Philosophical Society 2020
Footnotes
Supported by a grant from the Simons Foundation, #352034.


