Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T09:05:50.582Z Has data issue: false hasContentIssue false
  • English
  • Français

A second note on the simple group of order 6048

Published online by Cambridge University Press:  24 October 2008

W. L. Edge
W. L. Edge
Affiliation:
Mathematical Institute, 16 Chambers Street, Edinburgh 1
Get access Rights & Permissions [Opens in a new window]

Extract

1. The simple group of order 6048 has a permutation representation of degree 28 and two of degree 63. These are conspicuous in SU(3,32), the representation as a group of 3-rowed matrices, unitary and of determinant + 1, whose elements all belong to GF(32), or to J as we name this field. When these matrices as linear transformations in the projective plane ϖ over J they leave invariant the unit Hermitian form

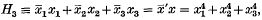
and the single capital U will henceforth signify the group so acting. There are 28 isotropic points n in ϖ satisfying H3 = 0; they furnish the representation of degree 28. The other 63 points p in ϖ are non-isotropic and furnish one of the representations of degree 63. The other is furnished by 63 triangles T; the vertices of a T are all p and every pair of them is linked in the antipolarity Π set up by H3; if their coordinate vectors are y and z then y′z = 0. Each p is a vertex of 3 T. These matters are fully explained in (7). Those points linked by II to a given point A are collinear, on the polar of A; no p lies on its polar, every n does. The polars t of points n are called tangents of H3 = 0, and the only isotropic point on t is its pole. The polars s of points p are secants of H3 = 0: each consists of 4 n with 3 pairs of linked p and, given s, it is these 3 pairs that complete those T having a vertex at the pole of s.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 1 , January 1963 , pp. 1 - 9
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Dickson, L. E.American J. Math. 26 (1904), 243–318.CrossRefGoogle Scholar
(2)Dickson, L. E.Math. Ann. 55 (1902), 521–572.CrossRefGoogle Scholar
(3)Dickson, L. E.Math. Ann. 60 (1905), 137–150.CrossRefGoogle Scholar
(4)Dyck, W.Math. Ann. 20 (1882), 1–44.CrossRefGoogle Scholar
(5)Edge, W. L.Proc. Roy. Soc. London, Ser. A, 222 (1953), 262–286.Google Scholar
(6)Edge, W. L.Canadian J. Math. 8 (1956), 362–382.CrossRefGoogle Scholar
(7)Edge, W. L.Proc. Cambridge Philos. Soc. 56 (1960), 189–204.CrossRefGoogle Scholar
(8)Frame, J. S.Ann. Mat. Pura Appl. (4), 32 (1951), 83–113.CrossRefGoogle Scholar
(9)Hesse, O. J.Reine Angew. Math. 49 (1855), 279–332.Google Scholar
(10)Klein, F.Math. Ann. 14 (1879), 428–471.CrossRefGoogle Scholar
(11)Klein, F.Gesammelte Math. Abh. III, 90–135.Google Scholar
(12)Klein, F. and Fricke, R.Vorlesungen über der Theorie der elliptischen Modulfunctionen. I (Leipzig, 1890).Google Scholar