Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T02:24:06.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform approximate solutions of certain nth-order differential equations. I

Published online by Cambridge University Press:  24 October 2008

J. Heading
J. Heading
Affiliation:
University of Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

Exact analytical solutions of certain second-order linear differential equations are often employed as approximate solutions of other second-order differential equations when the solutions of this latter equation cannot be expressed in terms of the standard transcendental functions. The classical exposition of this method has been given by Jeffreys (6); approximate solutions of the equation (using Jeffreys's notation)

are given in terms of solutions either of the equation

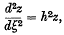
or of the equation

where h is a large parameter. A complete history of this technique is given in the author's recent text An introduction to phase-integral methods (Heading (5)).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 1 , January 1963 , pp. 95 - 110
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Heading, J.Proc. Cambridge Philos. Soc. 53 (1957), 399.CrossRefGoogle Scholar
(2)Heading, J.Proc. Cambridge Philos. Soc. 53 (1957), 419.CrossRefGoogle Scholar
(3)Heading, J.Proc. Cambridge Philos. Soc. 56 (1960), 329.CrossRefGoogle Scholar
(4)Heading, J.Quart. J. Mech. Appl. Math. 15 (1962), 215.CrossRefGoogle Scholar
(5)Heading, J.An introduction to phase-integral methods (Methuen; London, 1962).Google Scholar
(6)Jeffreys, H.Proc. Cambridge Philos. Soc. 49 (1953), 601.CrossRefGoogle Scholar