Research Article
Many-valued logical machines
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-321
-
- Article
- Export citation
A modified form of Siegel's mean value theorem. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 322-326
-
- Article
- Export citation
On prime-power groups with two generators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-337
-
- Article
- Export citation
On certain types of derivations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 338-345
-
- Article
- Export citation
A sufficient condition for the differentiation of certain classes of set functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 346-353
-
- Article
- Export citation
Norms of summation methods
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 354-357
-
- Article
- Export citation
Series expansions and general transforms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 358-367
-
- Article
- Export citation
The Spectral resolution of Watson transforms†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 368-376
-
- Article
- Export citation
A theorem of continuation for functions of several complex variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-382
-
- Article
- Export citation
Further computations of quadrupole line strengths
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-390
-
- Article
- Export citation
An application of the Weber-Orr transform to the problem of transonic flow past a finite wedge in a channel
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 391-395
-
- Article
- Export citation
Research Notes
A note on a theorem of Armand Borel
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 396-398
-
- Article
- Export citation
Front matter
PSP volume 54 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 54 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

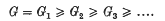




 has a norm, ‖
has a norm, ‖ 




