Article contents
Extending relational algebra with similarities
Published online by Cambridge University Press: 25 April 2012
Abstract
In this paper we propose various extensions to the relational model to support similarity-based querying. We build upon the 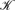 -relation model, where tuples are assigned values from an arbitrary semiring
-relation model, where tuples are assigned values from an arbitrary semiring 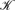 , and its associated positive relational algebra
, and its associated positive relational algebra 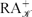 . We consider a recently proposed extension to
. We consider a recently proposed extension to 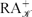 using a monus operation on the semiring to support negative queries, and show how, surprisingly, it fails for important ‘fuzzy’ semirings. Instead, we suggest using a negation operator. We also consider the identities satisfied by the relational algebra
using a monus operation on the semiring to support negative queries, and show how, surprisingly, it fails for important ‘fuzzy’ semirings. Instead, we suggest using a negation operator. We also consider the identities satisfied by the relational algebra 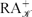 . We show that moving from a semiring to a particular form of lattice (a De Morgan frame) yields a relational algebra that satisfies all the classical (positive) relational algebra identities. We claim that to support real-world similarity queries realistically, one must move from tuple-level annotations to attribute-level annotations. We show in detail how our De Morgan frame-based model can be extended to support attribute-level annotations and give worked examples of similarity queries in this setting.
. We show that moving from a semiring to a particular form of lattice (a De Morgan frame) yields a relational algebra that satisfies all the classical (positive) relational algebra identities. We claim that to support real-world similarity queries realistically, one must move from tuple-level annotations to attribute-level annotations. We show in detail how our De Morgan frame-based model can be extended to support attribute-level annotations and give worked examples of similarity queries in this setting.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 2
- Cited by

