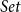1. Introduction
As functional languages have become increasingly sophisticated, so too have the data types they support. Algebraic data types (ADTs) – i.e., data types that are essentially tree types – are well-known to support an initial algebra semantics (IAS) in any category with enough structure (Manes and Arbib Reference Manes and Arbib1986). The IAS interpretation of an ADT comprises exactly the interpretations of the terms that are writable in its syntax. IAS interpretations of ADTs provide semantic justification for useful computational tools for programming with them, such as pattern matching, recursion rules, induction rules, etc. Also fundamental is that the interpretation of the type constructor defined by an ADT can be extended to a functor whose action on morphisms interprets the ADT’s syntactic map function. Categorical models in which ADTs have IAS interpretations include those of (Johann and Ghani Reference Johann and Ghani2007; Johann et al. Reference Johann, Ghiorzi and Jeffries2021; Manes and Arbib Reference Manes and Arbib1986). In the model of (Johann et al. Reference Johann, Ghiorzi and Jeffries2021), the syntactic generalization of ADTs known as nested types (Bird and Meertens Reference Bird, Meertens and Jeuring1998) also has IAS interpretations (Manes and Arbib Reference Manes and Arbib1986; nLab authors Reference Norell2019). Examples of nested types include perfect trees and bushes; see Section 3 below.
In addition to ADTs and nested types, modern functional languages such as Haskell, Agda, and OCaml support generalized algebraic data types (GADTs) (Peyton Jones et al. Reference Peyton Jones, Vytiniotis, Washburn and Weirich2006). As their name suggests, GADTs syntactically generalize nested types (and thus further generalize ADTs), so that

This sequence of syntactic generalizations suggests that a corresponding sequence of semantic generalizations might also hold. Specifically, since nested types (and thus ADTs) have IAS interpretations as functors on the category
![]() $\mathit{Set}$
of sets and functions between them, we might expect that there is also an IAS interpretation of GADTs as functors on
$\mathit{Set}$
of sets and functions between them, we might expect that there is also an IAS interpretation of GADTs as functors on
![]() $\mathit{Set}$
. Further, we might expect that this IAS of GADTs specializes to the standard IAS for nested types. Then, this interpretation of GADTs, like the standard IAS of nested types, would specialize to the standard IAS of ADTs. A semantic analogue of (1), if it existed, would formally justify the use of the word “generalized” in the moniker “generalized algebraic data type.”
$\mathit{Set}$
. Further, we might expect that this IAS of GADTs specializes to the standard IAS for nested types. Then, this interpretation of GADTs, like the standard IAS of nested types, would specialize to the standard IAS of ADTs. A semantic analogue of (1), if it existed, would formally justify the use of the word “generalized” in the moniker “generalized algebraic data type.”
In this paper, we show that, unfortunately, there is no semantic analogue of (1) because there is no reasonable IAS interpretation of GADTs as functors on
![]() $\mathit{Set}$
. A GADT programmer is likely to use GADTs precisely because they exhibit different behaviors at different types. They are therefore likely to consider a GADT to be completely specified by its syntax, i.e., to contain no data elements other than those writable in its syntax. But when GADTs are thought of in this way, the shape of a particular element of a GADT is actually determined by the data it contains. This is in marked contrast to the situation for ADTs and nested types, whose type uniformity gives rise to IAS interpretations that allow them to be regarded as type-independent containers that can be filled with data of any type. The main result of the first part of this paper shows that the type non-uniformity of GADTs entails that they cannot have IAS interpretations as functors on
$\mathit{Set}$
. A GADT programmer is likely to use GADTs precisely because they exhibit different behaviors at different types. They are therefore likely to consider a GADT to be completely specified by its syntax, i.e., to contain no data elements other than those writable in its syntax. But when GADTs are thought of in this way, the shape of a particular element of a GADT is actually determined by the data it contains. This is in marked contrast to the situation for ADTs and nested types, whose type uniformity gives rise to IAS interpretations that allow them to be regarded as type-independent containers that can be filled with data of any type. The main result of the first part of this paper shows that the type non-uniformity of GADTs entails that they cannot have IAS interpretations as functors on
![]() $\mathit{Set}$
without violating properties that we expect of models of languages that support them. In particular, Example 8 of Section 5 shows that a language supporting GADTs cannot have parametric models (Reynolds Reference Reynolds1983) in which GADTs are interpreted as functors on
$\mathit{Set}$
without violating properties that we expect of models of languages that support them. In particular, Example 8 of Section 5 shows that a language supporting GADTs cannot have parametric models (Reynolds Reference Reynolds1983) in which GADTs are interpreted as functors on
![]() $\mathit{Set}$
, at least not if those interpretations are to coincide with the standard IAS for those GADTs that are ADTs and nested types.Footnote 1 This finding is unintuitive, novel, and surprising.
$\mathit{Set}$
, at least not if those interpretations are to coincide with the standard IAS for those GADTs that are ADTs and nested types.Footnote 1 This finding is unintuitive, novel, and surprising.
The fact that GADTs do not have such specializable IAS interpretations as functors on
![]() $\mathit{Set}$
prompts us to consider interpreting GADTs as functors on other categories. Observing that mapping functions over elements of GADTs is notorious for being only partially defined (Johann and Cagne Reference Johann, Cagne and Sergey2022; Johann and Ghani Reference Johann and Ghani2008; Johann and Polonsky Reference Johann and Polonsky2019) compels us to seek IAS interpretations of GADTs as functors on categories with inherent notions of partiality. But since the IAS interpretation of a GADT should support pattern matching, recursion rules, induction rules, and other IAS-derived programming tools for that GADT, it should comprise exactly the interpretations of the terms that are writable in the GADT’s syntax. And since the IAS interpretation of a GADT should coincide with the standard IAS interpretation whenever the GADT is actually a nested type or an ADT, the semantic treatment of partial functions must specialize to the standard semantic treatment of everywhere-defined functions. The latter entails that we take our categories with inherent notions of partiality to have as subcategories the usual categories supporting IAS for nested types (including ADTs).
$\mathit{Set}$
prompts us to consider interpreting GADTs as functors on other categories. Observing that mapping functions over elements of GADTs is notorious for being only partially defined (Johann and Cagne Reference Johann, Cagne and Sergey2022; Johann and Ghani Reference Johann and Ghani2008; Johann and Polonsky Reference Johann and Polonsky2019) compels us to seek IAS interpretations of GADTs as functors on categories with inherent notions of partiality. But since the IAS interpretation of a GADT should support pattern matching, recursion rules, induction rules, and other IAS-derived programming tools for that GADT, it should comprise exactly the interpretations of the terms that are writable in the GADT’s syntax. And since the IAS interpretation of a GADT should coincide with the standard IAS interpretation whenever the GADT is actually a nested type or an ADT, the semantic treatment of partial functions must specialize to the standard semantic treatment of everywhere-defined functions. The latter entails that we take our categories with inherent notions of partiality to have as subcategories the usual categories supporting IAS for nested types (including ADTs).
A concrete example of such a category is the category
![]() $\mathit{PSet}$
of sets and partial functions between them. Indeed, this category has
$\mathit{PSet}$
of sets and partial functions between them. Indeed, this category has
![]() $\mathit{Set}$
as a subcategory, and its objects are precisely those of
$\mathit{Set}$
as a subcategory, and its objects are precisely those of
![]() $\mathit{Set}$
. Drawing inspiration from
$\mathit{Set}$
. Drawing inspiration from
![]() $\mathit{PSet}$
, in Section 6 we use the considerations of the previous paragraph to identify other categories that similarly capture computationally relevant notions of partiality. We consider the main feature of computationally relevant partiality to be that functions propagate undefinedness. This behavior is akin to that of functions that are strict in the sense of (Burn et al. Reference Burn, Hankin and Abramsky1986) and explicitly requiring it captures the computational expectation that a function cannot produce a value when given as an input an undefined value produced by a(nother) function. The main result of the second part of this paper is Theorem 18, which considers IAS interpretations of GADTs in categories equipped with computationally relevant notions of partiality. It shows that, in any such category, any extension to GADTs of the standard IAS for nested types in which the interpretations of the type constructors defined by GADTs extend to functors must be trivial.
$\mathit{PSet}$
, in Section 6 we use the considerations of the previous paragraph to identify other categories that similarly capture computationally relevant notions of partiality. We consider the main feature of computationally relevant partiality to be that functions propagate undefinedness. This behavior is akin to that of functions that are strict in the sense of (Burn et al. Reference Burn, Hankin and Abramsky1986) and explicitly requiring it captures the computational expectation that a function cannot produce a value when given as an input an undefined value produced by a(nother) function. The main result of the second part of this paper is Theorem 18, which considers IAS interpretations of GADTs in categories equipped with computationally relevant notions of partiality. It shows that, in any such category, any extension to GADTs of the standard IAS for nested types in which the interpretations of the type constructors defined by GADTs extend to functors must be trivial.
Taken together, the two main results of this paper lead us to conclude that GADTs cannot be interpreted as functors in any reasonable computational setting. So if a functorial semantics like the one we seek is possible, then it will be necessarily in a setting much more exotic than the ones GADT programmers are accustomed to using to understand their programs.
This paper is an extended version of the LSFA 2021 paper (Johann et al. Reference Johann, Ghiorzi and Jeffries2021). The results of Sections 2 through 5 were first reported by (Johann et al. Reference Johann, Ghiorzi and Jeffries2021), although they have been reworked here. The work in Section 6 is entirely new.
2. Syntax and Semantics of ADTs
A (unary) ADT has the formFootnote 2
where each
![]() $\mathsf{t_{ij}}$
is a type depending only on
$\mathsf{t_{ij}}$
is a type depending only on
![]() $\mathsf{a}$
. Such a data type can be thought of as a “container” for data of type
$\mathsf{a}$
. Such a data type can be thought of as a “container” for data of type
![]() $\mathsf{a}$
. The data in an ADT are arranged at various positions in its underlying shape, which is determined by the types of its constructors
$\mathsf{a}$
. The data in an ADT are arranged at various positions in its underlying shape, which is determined by the types of its constructors
![]() $\mathsf{C_1},\ldots,\mathsf{C_n}$
. An ADT’s constructors are used to build the data values of the data type, as well as to analyze those values using pattern matching. ADTs are used extensively in functional programming to structure computations, to express invariants of the data over which computations are defined, and to ensure the type safety of programs specifying those computations.
$\mathsf{C_1},\ldots,\mathsf{C_n}$
. An ADT’s constructors are used to build the data values of the data type, as well as to analyze those values using pattern matching. ADTs are used extensively in functional programming to structure computations, to express invariants of the data over which computations are defined, and to ensure the type safety of programs specifying those computations.
List types are the quintessential ADTs. The shape of the container underlying the type
is determined by the types of its two constructors
![]() $\mathsf{Nil\, ::\, List\, a}$
and
$\mathsf{Nil\, ::\, List\, a}$
and
![]() $\mathsf{Cons \,::\,a \to \mathsf{List}\,\,a\to List\,a}$
. These constructors specify that the data in a list of type
$\mathsf{Cons \,::\,a \to \mathsf{List}\,\,a\to List\,a}$
. These constructors specify that the data in a list of type
![]() $\mathsf{List\,a}$
are arranged linearly. The shape underlying the type
$\mathsf{List\,a}$
are arranged linearly. The shape underlying the type
![]() $\mathsf{List\,a}$
is therefore given by the set
$\mathsf{List\,a}$
is therefore given by the set
![]() $\mathbb{N}$
of natural numbers, with each natural number representing a choice of length for a list structure, and the positions in a structure of shape
$\mathbb{N}$
of natural numbers, with each natural number representing a choice of length for a list structure, and the positions in a structure of shape
![]() $\mathsf{n}$
given by natural numbers ranging from
$\mathsf{n}$
given by natural numbers ranging from
![]() $\mathsf{0}$
to
$\mathsf{0}$
to
![]() $\mathsf{n-1}$
. Since the type argument to every occurrence of the type constructor
$\mathsf{n-1}$
. Since the type argument to every occurrence of the type constructor
![]() $\mathsf{List}$
in the right-hand side of the above definition is the same as the type instance being defined on its left-hand side, the type
$\mathsf{List}$
in the right-hand side of the above definition is the same as the type instance being defined on its left-hand side, the type
![]() $\mathsf{List\,a}$
enforces the invariant that all of the data in a structure of this type have the same type
$\mathsf{List\,a}$
enforces the invariant that all of the data in a structure of this type have the same type
![]() $\mathsf{a}$
. In a similar way, the tree type
$\mathsf{a}$
. In a similar way, the tree type
of binary trees has as its underlying shape the type of binary trees of units, and the positions in a structure of this type are given by sequences of L (for “left”) and R (for “right”) navigating a path through the structure. The type
![]() $\mathsf{Tree\, a}$
enforces the invariant that all of the data at the nodes and leaves in a structure of this type have the same type
$\mathsf{Tree\, a}$
enforces the invariant that all of the data at the nodes and leaves in a structure of this type have the same type
![]() $\mathsf{a}$
.
$\mathsf{a}$
.
Since the shape of an ADT structure – i.e., a structure whose type is an instance of an ADT – is independent of the type of data it contains, ADTs can be defined polymorphically. As a result, an ADT structure containing data of type
![]() $\mathsf{a}$
can be transformed into another ADT structure of the exact same shape containing data of another type
$\mathsf{a}$
can be transformed into another ADT structure of the exact same shape containing data of another type
![]() $\mathsf{b}$
simply by applying a given function
$\mathsf{b}$
simply by applying a given function
![]() $\mathsf{f \,::\,a \to b}$
to each of its elements. In other words, for every ADT
$\mathsf{f \,::\,a \to b}$
to each of its elements. In other words, for every ADT
![]() $\mathsf{T\,a}$
, its underlying type constructor
$\mathsf{T\,a}$
, its underlying type constructor
![]() $\mathsf{T}$
can be made an instance of Haskell’s
$\mathsf{T}$
can be made an instance of Haskell’s
![]() $\mathsf{Functor}$
class by defining a type-and-data-uniform, structure-preserving, data-changing function
$\mathsf{Functor}$
class by defining a type-and-data-uniform, structure-preserving, data-changing function
![]() $\mathsf{map_T}$
for it.Footnote 3 Then, given a type-independent way of rearranging an ADT structure’s shape
$\mathsf{map_T}$
for it.Footnote 3 Then, given a type-independent way of rearranging an ADT structure’s shape
![]() $\mathsf{T\,a}$
into the shape for another ADT structure
$\mathsf{T\,a}$
into the shape for another ADT structure
![]() $\mathsf{T'\,a}$
, we get the same structure of type
$\mathsf{T'\,a}$
, we get the same structure of type
![]() $\mathsf{T'\,b}$
regardless of whether we first rearrange the original structure of type
$\mathsf{T'\,b}$
regardless of whether we first rearrange the original structure of type
![]() $\mathsf{T\,a}$
into one of type
$\mathsf{T\,a}$
into one of type
![]() $\mathsf{T'\,a}$
and then use
$\mathsf{T'\,a}$
and then use
![]() $\mathsf{map_{T'}}$
to convert that resulting structure to one of type
$\mathsf{map_{T'}}$
to convert that resulting structure to one of type
![]() $\mathsf{T'\,b}$
, or we first use
$\mathsf{T'\,b}$
, or we first use
![]() $\mathsf{map_T}$
to convert the original structure of type
$\mathsf{map_T}$
to convert the original structure of type
![]() $\mathsf{T\,a}$
to one of type
$\mathsf{T\,a}$
to one of type
![]() $\mathsf{T\,b}$
and then rearrange that resulting structure into one of type
$\mathsf{T\,b}$
and then rearrange that resulting structure into one of type
![]() $\mathsf{T'\,b}$
. For example, if
$\mathsf{T'\,b}$
. For example, if
![]() $\mathsf{f :: a \to b}$
,
$\mathsf{f :: a \to b}$
,
![]() $\mathsf{t \,::\,Tree\,a}$
, and
$\mathsf{t \,::\,Tree\,a}$
, and
![]() $\mathsf{g :: Tree\,c\to List\,c}$
is a polymorphic function (note that
$\mathsf{g :: Tree\,c\to List\,c}$
is a polymorphic function (note that
![]() $\mathsf{g}$
’s type is implicitly universally quantified over
$\mathsf{g}$
’s type is implicitly universally quantified over
![]() $\mathsf{c}$
) that arranges trees into lists in a type-independent way, then we have the following rearrange-transform property:
$\mathsf{c}$
) that arranges trees into lists in a type-independent way, then we have the following rearrange-transform property:
2.1 ADTs as functors
The standard way to understand ADTs is at least fixpointsFootnote 4 of (first-order) functors on the category interpreting types. This category is typically taken to be the category
![]() $\mathit{Set}$
, whose objects are sets and whose morphisms are functions between them, and we will do so here unless otherwise specified. But, as shown in (Johann and Polonsky Reference Johann and Polonsky2019), we can interpret types as objects in any locally presentable category (Adámek and Rosický Reference Adámek and Rosický1994) without affecting the development below.
$\mathit{Set}$
, whose objects are sets and whose morphisms are functions between them, and we will do so here unless otherwise specified. But, as shown in (Johann and Polonsky Reference Johann and Polonsky2019), we can interpret types as objects in any locally presentable category (Adámek and Rosický Reference Adámek and Rosický1994) without affecting the development below.
Syntactically, ADTs can be represented as fixpoints in any language with primitives for sum types, product types, and recursion. If
![]() $\mathsf{\mu }$
is the fixpoint operator in such a language, and if
$\mathsf{\mu }$
is the fixpoint operator in such a language, and if
![]() $\mathsf{1}$
is its unit type, then the fixpoint representations of the ADTs
$\mathsf{1}$
is its unit type, then the fixpoint representations of the ADTs
![]() $\mathsf{List\,a}$
and
$\mathsf{List\,a}$
and
![]() $\mathsf{Tree\,a}$
are
$\mathsf{Tree\,a}$
are
and
respectively. That is,
![]() $\mathsf{List\,a}$
can be seen as a fixpoint of
$\mathsf{List\,a}$
can be seen as a fixpoint of
![]() $\mathsf{F_{List\,a}}$
, where
$\mathsf{F_{List\,a}}$
, where
![]() $\mathsf{F_{List\,a}\,X} = \mathsf{1 + a \times X}$
, by (2), since
$\mathsf{F_{List\,a}\,X} = \mathsf{1 + a \times X}$
, by (2), since
Indeed, every element of
![]() $\mathsf{List\,a}$
is either empty or is obtained by consing an element of type
$\mathsf{List\,a}$
is either empty or is obtained by consing an element of type
![]() $\mathsf{a}$
onto an already-existing structure of type
$\mathsf{a}$
onto an already-existing structure of type
![]() $\mathsf{List\,a}$
, so that the above fixpoint equation is nothing more than a rewriting of the Haskell data type declaration for
$\mathsf{List\,a}$
, so that the above fixpoint equation is nothing more than a rewriting of the Haskell data type declaration for
![]() $\mathsf{List\,a}$
. Analogously,
$\mathsf{List\,a}$
. Analogously,
![]() $\mathsf{Tree\,a}$
can be seen as a fixpoint of
$\mathsf{Tree\,a}$
can be seen as a fixpoint of
![]() $\mathsf{F_{Tree\,a}}$
, where
$\mathsf{F_{Tree\,a}}$
, where
![]() $\mathsf{F_{Tree\,a}\,X} = \mathsf{a + X \times a \times X}$
, by (3). The intent here is that
$\mathsf{F_{Tree\,a}\,X} = \mathsf{a + X \times a \times X}$
, by (3). The intent here is that
![]() $\mathsf{List\, a}$
, i.e.,
$\mathsf{List\, a}$
, i.e.,
![]() $\mathsf{\mu F_{List\,a}}$
, should be interpreted by the semantic fixpoint
$\mathsf{\mu F_{List\,a}}$
, should be interpreted by the semantic fixpoint
![]() $\mu F_{\mathit{List}\,a}$
, where the functor
$\mu F_{\mathit{List}\,a}$
, where the functor
![]() $F_{\mathit{List}\,a}$
interprets the type constructor
$F_{\mathit{List}\,a}$
interprets the type constructor
![]() $\mathsf{F_{List\,a}}$
, and
$\mathsf{F_{List\,a}}$
, and
![]() $\mathsf{Tree\, a}$
, i.e.,
$\mathsf{Tree\, a}$
, i.e.,
![]() $\mathsf{ \mu F_{Tree\,a}}$
, should be interpreted by the semantic fixpoint
$\mathsf{ \mu F_{Tree\,a}}$
, should be interpreted by the semantic fixpoint
![]() $\mu F_{\mathit{Tree}\,a}$
, where the functor
$\mu F_{\mathit{Tree}\,a}$
, where the functor
![]() $F_{\mathit{Tree}\,a}$
interprets
$F_{\mathit{Tree}\,a}$
interprets
![]() $\mathsf{F_{Tree\,a}}$
.Footnote 5 A similar situation obtains for other ADTs.
$\mathsf{F_{Tree\,a}}$
.Footnote 5 A similar situation obtains for other ADTs.
The fixpoint equations above are entirely sensible at the level of types. But to ensure that the syntactic fixpoint representing an ADT actually denotes a semantic object computed as a semantic fixpoint, the corresponding semantic fixpoint calculation must converge. If, as is typical, we interpret our types as sets, then the fixpoint being taken must be of a functor on the category
![]() $\mathit{Set}$
of sets and functions between them, rather than merely of a function between sets nLab authors (2019). That is, the function
$\mathit{Set}$
of sets and functions between them, rather than merely of a function between sets nLab authors (2019). That is, the function
![]() $F$
interpreting the type constructor
$F$
interpreting the type constructor
![]() $\mathsf{F}$
constructing the body of a syntactic fixpoint must not only have an action on sets but must also have a functorial action on functions between sets. Reflecting this requirement back into syntax gives that
$\mathsf{F}$
constructing the body of a syntactic fixpoint must not only have an action on sets but must also have a functorial action on functions between sets. Reflecting this requirement back into syntax gives that
![]() $\mathsf{F}$
must support a function
$\mathsf{F}$
must support a function
![]() $\mathsf{map}$
satisfying the functor laws. That is,
$\mathsf{map}$
satisfying the functor laws. That is,
![]() $\mathsf{F}$
must be an instance of Haskell’s
$\mathsf{F}$
must be an instance of Haskell’s
![]() $\mathsf{Functor}$
class (with the aforementioned caveat about the functor laws).
$\mathsf{Functor}$
class (with the aforementioned caveat about the functor laws).
Requiring
![]() $F$
to be a functor is critical for the interpretation
$F$
to be a functor is critical for the interpretation
![]() $\mu F$
of the ADT
$\mu F$
of the ADT
![]() $\mathsf{T\,a} = \mathsf{\mu F}$
to exist. But to ensure that
$\mathsf{T\,a} = \mathsf{\mu F}$
to exist. But to ensure that
![]() $\mu F$
is itself a functor, so that the type constructor
$\mu F$
is itself a functor, so that the type constructor
![]() $\mathsf{T}$
associated with
$\mathsf{T}$
associated with
![]() $\mathsf{T\,a}$
also supports its own map function
$\mathsf{T\,a}$
also supports its own map function
![]() $\mathsf{map_T}$
, we can require that
$\mathsf{map_T}$
, we can require that
![]() $F$
be a functor on the category
$F$
be a functor on the category
![]() $\mathit{Set}^{\mathit{Set}}$
of functors and natural transformations on
$\mathit{Set}^{\mathit{Set}}$
of functors and natural transformations on
![]() $\mathit{Set}$
. That is, we can require that
$\mathit{Set}$
. That is, we can require that
![]() $F$
be a higher-order functor on
$F$
be a higher-order functor on
![]() $\mathit{Set}$
. Writing
$\mathit{Set}$
. Writing
![]() $H$
in place of
$H$
in place of
![]() $F$
to emphasize that it is higher-order, and reflecting this requirement back into syntax, we have that
$F$
to emphasize that it is higher-order, and reflecting this requirement back into syntax, we have that
![]() $\mathsf{T\,a} = \mathsf{(\mu H)\,a}$
for a “type constructor constructor”
$\mathsf{T\,a} = \mathsf{(\mu H)\,a}$
for a “type constructor constructor”
![]() $\mathsf{H}$
that supports suitableFootnote 6 map functions.
$\mathsf{H}$
that supports suitableFootnote 6 map functions.
A concrete example is given by the ADT
![]() $\mathsf{List\,a}$
. This type is modeled as the fixpoint
$\mathsf{List\,a}$
. This type is modeled as the fixpoint
![]() $\mu F_{\mathit{List\,a}}$
of the first-order functor whose action on sets is given by
$\mu F_{\mathit{List\,a}}$
of the first-order functor whose action on sets is given by
![]() $F_{\mathit{List}\,a}\,X = 1 + a \times X$
and whose action on functions is given by
$F_{\mathit{List}\,a}\,X = 1 + a \times X$
and whose action on functions is given by
![]() $F_{\mathit{List}\,a}\,f ={id}_1 +{id}_a \times f$
. The type constructor
$F_{\mathit{List}\,a}\,f ={id}_1 +{id}_a \times f$
. The type constructor
![]() $\mathsf{List}$
is modeled by the functor that is the fixpoint
$\mathsf{List}$
is modeled by the functor that is the fixpoint
![]() $\mu H$
of the higher-order functor
$\mu H$
of the higher-order functor
![]() $H$
whose action on a functor
$H$
whose action on a functor
![]() $F$
is given by the functor
$F$
is given by the functor
![]() $H\,F$
whose actions on sets and functions between them are given by
$H\,F$
whose actions on sets and functions between them are given by
![]() $H\,F\,X = 1 + X \times F\,X$
and
$H\,F\,X = 1 + X \times F\,X$
and
![]() $H\,F\,f ={id}_1 + f \times F\,f$
, respectively, and whose action on a natural transformation
$H\,F\,f ={id}_1 + f \times F\,f$
, respectively, and whose action on a natural transformation
![]() $\eta$
is the natural transformation whose component at
$\eta$
is the natural transformation whose component at
![]() $X$
is given by
$X$
is given by
![]() $(H\,\eta )_X ={id}_1 +{id}_X \times \eta _X$
. Reflecting the functorial action of
$(H\,\eta )_X ={id}_1 +{id}_X \times \eta _X$
. Reflecting the functorial action of
![]() $\mu H$
back into syntax gives exactly Haskell’s built-in
$\mu H$
back into syntax gives exactly Haskell’s built-in
![]() $\mathsf{map}$
function as the type-and-data-uniform, structure-preserving, data-changing function associated with
$\mathsf{map}$
function as the type-and-data-uniform, structure-preserving, data-changing function associated with
![]() $\mathsf{List}$
.
$\mathsf{List}$
.
Note that the rearrange-transform property for fixpoint representations of ADTs is simply the reflection back into syntax of the instance of naturality for the type-independent function that rearranges structures of type
![]() $\mathsf{T\,a}$
into ones of type
$\mathsf{T\,a}$
into ones of type
![]() $\mathsf{T'\,a}$
and the structure-preserving, data-changing functions
$\mathsf{T'\,a}$
and the structure-preserving, data-changing functions
![]() $\mathsf{map_T\,f}$
and
$\mathsf{map_T\,f}$
and
![]() $\mathsf{map_{T'}\,f}$
for a function
$\mathsf{map_{T'}\,f}$
for a function
![]() $\mathsf{f :: a \to b}$
, where
$\mathsf{f :: a \to b}$
, where
![]() $\mathsf{T}$
and
$\mathsf{T}$
and
![]() $\mathsf{T'}$
are the type constructors associated with these ADTs, respectively.
$\mathsf{T'}$
are the type constructors associated with these ADTs, respectively.
Whenever a data type has an interpretation as the least fixpoint of a functor – or, equivalently by Lambek’s Lemma, as the carrier of the initial algebra of that functor – we say that the data type has an initial algebra semantics (IAS). As mentioned in Section 1, ADTs and nested types are well-known to have IAS (Johann and Ghani Reference Johann and Ghani2007; Johann et al. Reference Johann, Ghiorzi and Jeffries2021; Manes and Arbib Reference Manes and Arbib1986). Having an IAS is the gold standard semantics for a data type: an IAS guarantees that the data type supports pattern matching on its constructors, an induction rule that can be used to prove properties on it, an elimination rule guaranteeing that functions over it can be written by recursion, etc. These essential programming tools are just reflections back into syntax of fundamental properties of IAS.
3. Syntax and Semantics of GADTs
Generalized algebraic data types (GADTs) (Peyton Jones et al. Reference Peyton Jones, Vytiniotis, Washburn and Weirich2006) relax the restriction on the type instances appearing in a data type definition. The special form of GADTs known as nested types (Bird and Meertens Reference Bird, Meertens and Jeuring1998) allows the data constructors of a GADT to take as arguments data whose types involve type instances of the GADT other than the one being defined. However, the return type of each constructor of a nested type must still be precisely the one being defined. This is illustrated by the definition
of the nested type
![]() $\mathsf{PTree\,a}$
of perfect trees, which introduces the data constructors
$\mathsf{PTree\,a}$
of perfect trees, which introduces the data constructors
![]() $\mathsf{PLeaf :: a \to PTree\,a}$
and
$\mathsf{PLeaf :: a \to PTree\,a}$
and
![]() $\mathsf{PNode :: PTree \,(a\times a) \to PTree\,a}$
. It enforces not only the invariant that all of the data in a structure of type
$\mathsf{PNode :: PTree \,(a\times a) \to PTree\,a}$
. It enforces not only the invariant that all of the data in a structure of type
![]() $\mathsf{PTree\,a}$
is of the same type
$\mathsf{PTree\,a}$
is of the same type
![]() $\mathsf{a}$
but also the invariant that all perfect trees have lengths that are powers of 2. GADTs allow their constructors both to take as arguments and return as results data whose types involve type instances of the GADT other than the one being defined. An example of a GADT is
$\mathsf{a}$
but also the invariant that all perfect trees have lengths that are powers of 2. GADTs allow their constructors both to take as arguments and return as results data whose types involve type instances of the GADT other than the one being defined. An example of a GADT is
![]() $\mathsf{Seq}$
, whose definition is
$\mathsf{Seq}$
, whose definition is
 \begin{equation} \begin{array}{l} \mathsf{data\, Seq\,a\,where}\\ \mathsf{\;\;\;\;\;\;\;\;Const ::\, a \to Seq\,a}\\ \mathsf{\;\;\;\;\;\;\;\;Pair\,\,\,\,::\, Seq \,a \to Seq\,b \to Seq\,(a \times b)}\\ \end{array} \end{equation}
\begin{equation} \begin{array}{l} \mathsf{data\, Seq\,a\,where}\\ \mathsf{\;\;\;\;\;\;\;\;Const ::\, a \to Seq\,a}\\ \mathsf{\;\;\;\;\;\;\;\;Pair\,\,\,\,::\, Seq \,a \to Seq\,b \to Seq\,(a \times b)}\\ \end{array} \end{equation}
Since the return type of the data constructor
![]() $\mathsf{Pair}$
is not of the form
$\mathsf{Pair}$
is not of the form
![]() $\mathsf{Seq\,a}$
for any variable
$\mathsf{Seq\,a}$
for any variable
![]() $\mathsf{a}$
,
$\mathsf{a}$
,
![]() $\mathsf{Seq}$
is a proper GADT, i.e., a GADT that is not a nested type.
$\mathsf{Seq}$
is a proper GADT, i.e., a GADT that is not a nested type.
By contrast with the ADT
![]() $\mathsf{List\, a}$
, where the type parameter
$\mathsf{List\, a}$
, where the type parameter
![]() $\mathsf{a}$
is integral to the type being defined, the type parameter
$\mathsf{a}$
is integral to the type being defined, the type parameter
![]() $\mathsf{a}$
appears in both
$\mathsf{a}$
appears in both
![]() $\mathsf{PTree\,a}$
and
$\mathsf{PTree\,a}$
and
![]() $\mathsf{Seq\,a}$
as a “dummy” parameter used only to give the kind
$\mathsf{Seq\,a}$
as a “dummy” parameter used only to give the kind
![]() $\mathsf{* \to *}$
of the type constructors
$\mathsf{* \to *}$
of the type constructors
![]() $\mathsf{PTree}$
and
$\mathsf{PTree}$
and
![]() $\mathsf{Seq}$
. This is explicitly captured in the alternative “kind signature” Haskell syntax, which represents
$\mathsf{Seq}$
. This is explicitly captured in the alternative “kind signature” Haskell syntax, which represents
![]() $\mathsf{PTree}$
and
$\mathsf{PTree}$
and
![]() $\mathsf{Seq}$
as
$\mathsf{Seq}$
as
 \begin{equation*}\begin {array}{l} \mathsf {data\, PTree :: * \to *\,where}\\ \mathsf {\;\;\;\;\;\;\;\;PLeaf \,\,\,\;::\, a \to PTree\,a}\\ \mathsf {\;\;\;\;\;\;\;\;PNode\,\, ::\, PTree \,(a \times a) \to PTree\,a}\\ \end {array}\end{equation*}
\begin{equation*}\begin {array}{l} \mathsf {data\, PTree :: * \to *\,where}\\ \mathsf {\;\;\;\;\;\;\;\;PLeaf \,\,\,\;::\, a \to PTree\,a}\\ \mathsf {\;\;\;\;\;\;\;\;PNode\,\, ::\, PTree \,(a \times a) \to PTree\,a}\\ \end {array}\end{equation*}
and
 \begin{equation*}\begin {array}{l} \mathsf {data\, Seq :: * \to *\,where}\\ \mathsf {\;\;\;\;\;\;\;\;Const ::\, a \to Seq\,a}\\ \mathsf {\;\;\;\;\;\;\;\;Pair\,\,\,\,\; ::\, Seq \,a \to Seq\,b \to Seq\,(a \times b)}\\ \end {array}\end{equation*}
\begin{equation*}\begin {array}{l} \mathsf {data\, Seq :: * \to *\,where}\\ \mathsf {\;\;\;\;\;\;\;\;Const ::\, a \to Seq\,a}\\ \mathsf {\;\;\;\;\;\;\;\;Pair\,\,\,\,\; ::\, Seq \,a \to Seq\,b \to Seq\,(a \times b)}\\ \end {array}\end{equation*}
respectively. A GADT – even a nested type – thus does not define a family of inductive types, one for each type argument, like an ADT does, but instead defines an entire family of types that must be constructed simultaneously. That is, a GADT defines an inductive family of types. Letting
![]() $*^{{n}} \to *$
denote
$*^{{n}} \to *$
denote
![]() $\overset{n\text{ asterisks}}{\overbrace{* \to * \to \dots \to *}} \to *$
, we take the general form of a GADT to be
$\overset{n\text{ asterisks}}{\overbrace{* \to * \to \dots \to *}} \to *$
, we take the general form of a GADT to be
 \begin{equation} \begin{array}{l} \!\textsf{data}\ \textsf{G} :: *^{n} \to *\ \textsf{where} \\ \;\;\;\;\;\;\;\; \textsf{C}_{\textsf{l}}\, :: \ \textsf{F}_{\textsf{l}}\,\overline{\textsf{a}_{\textsf{l}}} \to \textsf{G} \,\overline{\textsf{K}_{\textsf{l}}\,\overline{\textsf{a}_{\textsf{l}}}} \\ \;\;\;\;\;\;\;\; \vdots \\ \;\;\;\;\;\;\;\; \textsf{C}_{m}\, ::\ \textsf{F}_{m}\,\overline{\textsf{a}_{m}} \to \textsf{G}\, \overline{\textsf{K}_{m}\,\overline{\textsf{a}_{m}}} \end{array} \end{equation}
\begin{equation} \begin{array}{l} \!\textsf{data}\ \textsf{G} :: *^{n} \to *\ \textsf{where} \\ \;\;\;\;\;\;\;\; \textsf{C}_{\textsf{l}}\, :: \ \textsf{F}_{\textsf{l}}\,\overline{\textsf{a}_{\textsf{l}}} \to \textsf{G} \,\overline{\textsf{K}_{\textsf{l}}\,\overline{\textsf{a}_{\textsf{l}}}} \\ \;\;\;\;\;\;\;\; \vdots \\ \;\;\;\;\;\;\;\; \textsf{C}_{m}\, ::\ \textsf{F}_{m}\,\overline{\textsf{a}_{m}} \to \textsf{G}\, \overline{\textsf{K}_{m}\,\overline{\textsf{a}_{m}}} \end{array} \end{equation}
Here, for each
![]() $i \in \{1,\ldots,m\}$
,
$i \in \{1,\ldots,m\}$
,
![]() $\mathsf{F}_i$
is a type constructor with type signature
$\mathsf{F}_i$
is a type constructor with type signature
![]() $*^{n_i} \to *$
that can involve
$*^{n_i} \to *$
that can involve
![]() $\textsf{G}$
itself, and each component
$\textsf{G}$
itself, and each component
![]() ${\overline{\mathsf{K}_i}}_j$
of
${\overline{\mathsf{K}_i}}_j$
of
![]() $\overline{\mathsf{K}_i}$
is either a projection or a type constructor in the language without GADTs whose type signature is
$\overline{\mathsf{K}_i}$
is either a projection or a type constructor in the language without GADTs whose type signature is
![]() $*^{n_i} \to *$
. In general, a type constructor
$*^{n_i} \to *$
. In general, a type constructor
![]() $\mathsf{T}$
with type signature
$\mathsf{T}$
with type signature
![]() $*^{k} \to *$
is said to have arity
$*^{k} \to *$
is said to have arity
![]() $k$
. The overline notation denotes a finite list whose length is exactly the arity of the type constructor being applied to it. The number of type constructors in each
$k$
. The overline notation denotes a finite list whose length is exactly the arity of the type constructor being applied to it. The number of type constructors in each
![]() $\overline{\mathsf{K}_i}$
is thus
$\overline{\mathsf{K}_i}$
is thus
![]() $n$
, and the number of type variables in
$n$
, and the number of type variables in
![]() $\overline{\mathsf{a}_i}$
is thus
$\overline{\mathsf{a}_i}$
is thus
![]() $n_i$
. In addition, we require that each type constructor
$n_i$
. In addition, we require that each type constructor
![]() $\mathsf{F}_i$
is constructed inductively according to the following grammar, where
$\mathsf{F}_i$
is constructed inductively according to the following grammar, where
![]() $p$
ranges from
$p$
ranges from
![]() $1$
to the length of
$1$
to the length of
![]() $\overline{\textsf{a}}$
:
$\overline{\textsf{a}}$
:
This grammar is subject to the following restrictions. In the fourth clause, neither
![]() $\textsf{G}$
nor any (other) proper GADT appears in
$\textsf{G}$
nor any (other) proper GADT appears in
![]() $\mathsf{F}$
, and
$\mathsf{F}$
, and
![]() $\textsf{L}$
is a closed type. In the fifth clause, neither
$\textsf{L}$
is a closed type. In the fifth clause, neither
![]() $\textsf{G}$
nor any (other) proper GADT appears in any of the
$\textsf{G}$
nor any (other) proper GADT appears in any of the
![]() $n$
type constructors in
$n$
type constructors in
![]() $\overline{\mathsf{F}}$
. These requirements prevent the nesting of proper GADTs, which would not only render the ambient language inconsistent (Norell Reference Norell2022) but would also make it impossible to obtain a parametricity theorem for any language extended with GADTs. In the sixth clause,
$\overline{\mathsf{F}}$
. These requirements prevent the nesting of proper GADTs, which would not only render the ambient language inconsistent (Norell Reference Norell2022) but would also make it impossible to obtain a parametricity theorem for any language extended with GADTs. In the sixth clause,
![]() $\textsf{H} :: *^{k} \to *$
is a data type constructor defined by any nested type (including truly nested types). It thus subsumes the case in which
$\textsf{H} :: *^{k} \to *$
is a data type constructor defined by any nested type (including truly nested types). It thus subsumes the case in which
![]() $\textsf{F}\,\overline{\textsf{a}}$
is a closed type.
$\textsf{F}\,\overline{\textsf{a}}$
is a closed type.
All of the particular GADTs considered in this paper conform to the syntax in (5). In addition to specifying the syntax of the GADTs we consider, we also assume that GADTs come equipped with constructs for defining functions (uniquely) over them. More precisely, each
![]() $n$
-ary GADT
$n$
-ary GADT
![]() $\textsf{G}$
comes together with a rule of the following form:
$\textsf{G}$
comes together with a rule of the following form:
 \begin{align} \text{ Given a type expression } \textsf{E}\, \overline{\textsf{a}}, \text{ whose } n \text{ free type variables are the components of} \\ \overline{\textsf{a}}, \text{ and terms } \textsf{t}_{i} :: \forall \overline{\textsf{a}_{\textsf{i}}}.\ \textsf{F}_{\textsf{i}}\,\overline{\textsf{a}_{\textsf{i}}} \to \textsf{E}\, \overline{\textsf{K}_{\textsf{i}}}\,\overline{\textsf{a}_{\textsf{i}}} \text{ for each } i \in \{1,\ldots,m\}, \text{ there is a unique }\nonumber \\ \text{ term } \textsf{t} :: \forall \overline{\textsf{a}}.\ \textsf{G}\,\overline{\textsf{a}} \to \textsf{E}\, \overline{\textsf{a}} \text{ such that } \textsf{t} \circ \textsf{c}_{i} = \textsf{t}_{i} \text{ for each } i \in \{1,\ldots,m\}. \nonumber \end{align}
\begin{align} \text{ Given a type expression } \textsf{E}\, \overline{\textsf{a}}, \text{ whose } n \text{ free type variables are the components of} \\ \overline{\textsf{a}}, \text{ and terms } \textsf{t}_{i} :: \forall \overline{\textsf{a}_{\textsf{i}}}.\ \textsf{F}_{\textsf{i}}\,\overline{\textsf{a}_{\textsf{i}}} \to \textsf{E}\, \overline{\textsf{K}_{\textsf{i}}}\,\overline{\textsf{a}_{\textsf{i}}} \text{ for each } i \in \{1,\ldots,m\}, \text{ there is a unique }\nonumber \\ \text{ term } \textsf{t} :: \forall \overline{\textsf{a}}.\ \textsf{G}\,\overline{\textsf{a}} \to \textsf{E}\, \overline{\textsf{a}} \text{ such that } \textsf{t} \circ \textsf{c}_{i} = \textsf{t}_{i} \text{ for each } i \in \{1,\ldots,m\}. \nonumber \end{align}
This will be important in the proof of Theorem 18 below.
Proper GADTs are used in precisely those situations in which different behaviors at different instances of a data type are desired. This is achieved by allowing the programmer to give the type signatures of the GADT’s data constructors independently – as is made explicit by the alternative syntax above – and then using pattern matching to force the desired type refinement. The same technique can be used to support type-indexed inductive families in dependent type theory. Note, however, that the impredicative nature of languages supporting GADTs entails they behave quite differently from those supporting type-indexed inductive families.
Applications of GADTs include generic programming, modeling programming languages via higher-order abstract syntax, maintaining invariants in data structures, and expressing constraints in embedded domain-specific languages. GADTs have also been used, e.g., to implement tagless interpreters (Pasalic and Linger Reference Pasalic, Linger and Gabor Karsai2004; Peyton Jones et al. Reference Peyton Jones, Vytiniotis, Washburn and Weirich2006; Pottier and Régis-Gianas Reference Pottier and Régis-Gianas2006), to improve memory performance (Minsky Reference Minsky2015), and to design APIs (Penner Reference Penner2020).
3.1 GADTs are not functors
In this section, we show that, by contrast with the situation for ADTs and nested types, proper GADTs do not support map functions. That is, since proper GADTs are not uniform in their type parameters, they cannot be regarded as type-independent containers that can be filled with data of any type the way that ADTs and nested types can. But since a GADT’s map function is just the reflection back into syntax of the functorial action of the functor interpreting it, this entails that, by contrast with the situation for ADTs and nested types, proper GADT syntax cannot be interpreted as functors on
![]() $\mathit{Set}$
. We will consider various approaches to recovering functorial interpretations of GADTs in the remainder of the paper.
$\mathit{Set}$
. We will consider various approaches to recovering functorial interpretations of GADTs in the remainder of the paper.
Example 1.
The GADT
![]() $\mathsf{Seq}$
defined in (4) comprises sequences of any type
$\mathsf{Seq}$
defined in (4) comprises sequences of any type
![]() $\mathsf{a}$
, and sequences obtained by pairing the data in two already-existing sequences. Syntactically,
$\mathsf{a}$
, and sequences obtained by pairing the data in two already-existing sequences. Syntactically,
![]() $\mathsf{Seq}$
contains no elements other than these. We naturally expect a GADT’s interpretation, like those for ADTs and nested types, to contain only those data elements that are representable by its syntax. However, the definition in (4) specifies that an element of
$\mathsf{Seq}$
contains no elements other than these. We naturally expect a GADT’s interpretation, like those for ADTs and nested types, to contain only those data elements that are representable by its syntax. However, the definition in (4) specifies that an element of
![]() $\mathsf{Seq}$
of the form
$\mathsf{Seq}$
of the form
![]() $\mathsf{Pair\,t}_1\,\mathsf{t}_2$
must have the shape of a sequence of data of pair type rather than a sequence of data of an arbitrary type. This means that the clause of
$\mathsf{Pair\,t}_1\,\mathsf{t}_2$
must have the shape of a sequence of data of pair type rather than a sequence of data of an arbitrary type. This means that the clause of
![]() $\mathsf{map}$
for the
$\mathsf{map}$
for the
![]() $\mathsf{Pair}$
constructor should feed
$\mathsf{Pair}$
constructor should feed
![]() $\mathsf{map}$
a function
$\mathsf{map}$
a function
![]() $\mathsf{f :: (a \times b) \to c}$
and a term of the form
$\mathsf{f :: (a \times b) \to c}$
and a term of the form
![]() $\mathsf{Pair \,t}_1\,\mathsf{t}_2$
for
$\mathsf{Pair \,t}_1\,\mathsf{t}_2$
for
![]() $\mathsf{t}_1 \mathsf{:: Seq\,a}$
and
$\mathsf{t}_1 \mathsf{:: Seq\,a}$
and
![]() $\mathsf{t}_2\mathsf{:: Seq\,b}$
, and produce a term
$\mathsf{t}_2\mathsf{:: Seq\,b}$
, and produce a term
![]() $\mathsf{Pair\,t}_3\,\mathsf{t}_4$
for some appropriately typed terms
$\mathsf{Pair\,t}_3\,\mathsf{t}_4$
for some appropriately typed terms
![]() $\mathsf{t}_3$
and
$\mathsf{t}_3$
and
![]() $\mathsf{t}_4$
. However, it is not clear how to achieve this since
$\mathsf{t}_4$
. However, it is not clear how to achieve this since
![]() $\mathsf{c}$
need not necessarily be a product type. And even if
$\mathsf{c}$
need not necessarily be a product type. And even if
![]() $\mathsf{c}$
were known to be of the form
$\mathsf{c}$
were known to be of the form
![]() $\mathsf{w \times z}$
, we still wouldn’t necessarily have a way to produce data of type
$\mathsf{w \times z}$
, we still wouldn’t necessarily have a way to produce data of type
![]() $\mathsf{w \times z}$
from only
$\mathsf{w \times z}$
from only
![]() $\mathsf{f :: a \times b \to w \times z}$
and
$\mathsf{f :: a \times b \to w \times z}$
and
![]() $\mathsf{t}_1$
and
$\mathsf{t}_1$
and
![]() $\mathsf{t}_2$
unless we knew, e.g., that
$\mathsf{t}_2$
unless we knew, e.g., that
![]() $\mathsf{f}$
was a product
$\mathsf{f}$
was a product
![]() $\mathsf{(f}_1 \mathsf{:: a \to w) \times (f}_2 \mathsf{:: b \to z)}$
of functions. Since
$\mathsf{(f}_1 \mathsf{:: a \to w) \times (f}_2 \mathsf{:: b \to z)}$
of functions. Since
![]() $\mathsf{Seq}$
does not support a map function, it cannot be made into a functor.
$\mathsf{Seq}$
does not support a map function, it cannot be made into a functor.
As already noted, the fact that the syntax of GADTs allows non-variable type arguments in the return types of their data constructors establishes a strong connection between a GADT’s shape and the data it contains. With ADTs, we first choose the shape of the container and then fill that container with data of whatever type we like; critically, the choice of shape is independent of the data to be stored. With GADTs, however, the shape of the container may actually depend on (the type of) the data to be contained. For example,
![]() $\mathsf{Const}$
can create data of any shape
$\mathsf{Const}$
can create data of any shape
![]() $\mathsf{Seq\,a}$
, but
$\mathsf{Seq\,a}$
, but
![]() $\mathsf{Pair}$
can produce data of shape
$\mathsf{Pair}$
can produce data of shape
![]() $\mathsf{Seq\,a}$
only if
$\mathsf{Seq\,a}$
only if
![]() $\mathsf{a}$
is a pair type. As a result, modifying the data in a GADT’s container may change the shape of that container, or even produce an ill-typed result.
$\mathsf{a}$
is a pair type. As a result, modifying the data in a GADT’s container may change the shape of that container, or even produce an ill-typed result.
To determine the possible shapes of a GADT’s container, we must pattern match the type of the data to be contained. For this, it is essential that a GADT calculus supports an equality type
![]() $\mathsf{Eq}$
. This type is a singleton set when its two type arguments are the same and is the empty set otherwise. That is, it is the syntactic reflection of semantic equality function
$\mathsf{Eq}$
. This type is a singleton set when its two type arguments are the same and is the empty set otherwise. That is, it is the syntactic reflection of semantic equality function
![]() $\mathit{Eq}$
. Then, every GADT can be written in terms of
$\mathit{Eq}$
. Then, every GADT can be written in terms of
![]() $\mathsf{Eq}$
(Cheney and Hinze Reference Cheney and Hinze2003; Hinze Reference Hinze2003; McBride Reference McBride1999; Schrijvers et al. Reference Schrijvers, Jones, Sulzmann and Vytiniotis2009; Sheard and Pasalic Reference Sheard and Pasalic2004), so that
$\mathsf{Eq}$
(Cheney and Hinze Reference Cheney and Hinze2003; Hinze Reference Hinze2003; McBride Reference McBride1999; Schrijvers et al. Reference Schrijvers, Jones, Sulzmann and Vytiniotis2009; Sheard and Pasalic Reference Sheard and Pasalic2004), so that
![]() $\mathsf{Eq}$
is, in some sense, the quintessential GADT. Unfortunately, however,
$\mathsf{Eq}$
is, in some sense, the quintessential GADT. Unfortunately, however,
![]() $\mathsf{Eq}$
itself cannot be interpreted as a functor on
$\mathsf{Eq}$
itself cannot be interpreted as a functor on
![]() $\mathit{Set}$
, as the next example shows.
$\mathit{Set}$
, as the next example shows.
Example 2.
The equality GADT
![]() $\mathsf{Eq}$
is defined by
$\mathsf{Eq}$
is defined by
This GADT cannot be made into a functor: if
![]() $\mathsf{Eq}$
supported a function
$\mathsf{Eq}$
supported a function
then defining
would allow us to construct an element
of the empty type
![]() $\mathsf{0}$
, where
$\mathsf{0}$
, where
![]() $\mathsf{1}$
is (by abuse of notation) the unique element of the unit type
$\mathsf{1}$
is (by abuse of notation) the unique element of the unit type
![]() $\mathsf{1}$
, and
$\mathsf{1}$
, and
![]() $\mathsf{absurd :: 0 \to 1}$
is the empty function. But this is not possible.
$\mathsf{absurd :: 0 \to 1}$
is the empty function. But this is not possible.
Since a proper GADT can always be written in terms of
![]() $\mathsf{Eq}$
, its map function must necessarily involve
$\mathsf{Eq}$
, its map function must necessarily involve
![]() $\mathsf{Eq}$
’s map function, too. But since the
$\mathsf{Eq}$
’s map function, too. But since the
![]() $\mathsf{Eq}$
does not support a map function, it is immediate that GADTs cannot, in general, support map functions either. For
$\mathsf{Eq}$
does not support a map function, it is immediate that GADTs cannot, in general, support map functions either. For
![]() $\mathsf{Seq}$
, this can be seen by noting that, given a function
$\mathsf{Seq}$
, this can be seen by noting that, given a function
![]() $\mathsf{f :: (a \times b) \to c}$
, the term
$\mathsf{f :: (a \times b) \to c}$
, the term
![]() $\mathsf{map_{Eq\,(a \times b)}\,f\, Refl}$
would have type
$\mathsf{map_{Eq\,(a \times b)}\,f\, Refl}$
would have type
![]() $\mathsf{Eq\,(a \times b)\,c}$
. But, as above, we have no way to produce a term of this type in the absence of a functorial map function for
$\mathsf{Eq\,(a \times b)\,c}$
. But, as above, we have no way to produce a term of this type in the absence of a functorial map function for
![]() $\mathsf{Eq}$
, and thus no way to produce a term of type
$\mathsf{Eq}$
, and thus no way to produce a term of type
![]() $\mathsf{Seq\,c}$
using the
$\mathsf{Seq\,c}$
using the
![]() $\mathsf{Pair}$
constructor, as is required by the clause of
$\mathsf{Pair}$
constructor, as is required by the clause of
![]() $\mathsf{map_{Seq}}$
for
$\mathsf{map_{Seq}}$
for
![]() $\mathsf{Pair}$
. A similar analysis is obtained for other proper GADTs.
$\mathsf{Pair}$
. A similar analysis is obtained for other proper GADTs.
4. Recovering Functoriality
One way to read the results of Section 3.1 is as saying that, if we want to interpret types in
![]() $\mathit{Set}$
, then we must be willing to accept that the interpretations of proper GADTs will necessarily contain “extra” elements that are not reachable in syntax. We will call such extra elements in the semantics ghost elements. The functorial completion (Johann and Polonsky Reference Johann and Polonsky2019) of a GADT adds ghost elements to complete the interpretation of its syntax from a function on types to a functor on types. As we have seen, functoriality is absolutely essential to the initial algebra semantics of data types.
$\mathit{Set}$
, then we must be willing to accept that the interpretations of proper GADTs will necessarily contain “extra” elements that are not reachable in syntax. We will call such extra elements in the semantics ghost elements. The functorial completion (Johann and Polonsky Reference Johann and Polonsky2019) of a GADT adds ghost elements to complete the interpretation of its syntax from a function on types to a functor on types. As we have seen, functoriality is absolutely essential to the initial algebra semantics of data types.
Since being a functor entails supporting a map function satisfying the functor laws, the functorial interpretation of a data type must include the entire “map closure” of its syntax. Intuitively, this means that the functorial interpretation of
![]() $\mathsf{Eq}$
, for example, contains not just interpretations of those data elements representable by its syntax, but also interpretations of all data elements of the form
$\mathsf{Eq}$
, for example, contains not just interpretations of those data elements representable by its syntax, but also interpretations of all data elements of the form
![]() $\mathsf{map_{Eq}\,f\,g\,s}$
for all types
$\mathsf{map_{Eq}\,f\,g\,s}$
for all types
![]() $\mathsf{t_1}$
,
$\mathsf{t_1}$
,
![]() $\mathsf{t_2}$
,
$\mathsf{t_2}$
,
![]() $\mathsf{t_3}$
, and
$\mathsf{t_3}$
, and
![]() $\mathsf{t_4}$
, all functions
$\mathsf{t_4}$
, all functions
![]() $\mathsf{f :: t_1 \to t_3}$
and
$\mathsf{f :: t_1 \to t_3}$
and
![]() $\mathsf{g :: t_2 \to t_4}$
definable in the language, and all
$\mathsf{g :: t_2 \to t_4}$
definable in the language, and all
![]() $\mathsf{s :: Eq\,t_1\,t_2}$
, as well as all interpretations of data elements of the form
$\mathsf{s :: Eq\,t_1\,t_2}$
, as well as all interpretations of data elements of the form
![]() $\mathsf{map_{Eq}\,h\,k\,s'}$
for all appropriately typed functions
$\mathsf{map_{Eq}\,h\,k\,s'}$
for all appropriately typed functions
![]() $\mathsf{h}$
and
$\mathsf{h}$
and
![]() $\mathsf{k}$
and each element
$\mathsf{k}$
and each element
![]() $\mathsf{s'}$
already added to the data type, and so on. Functorial completion for
$\mathsf{s'}$
already added to the data type, and so on. Functorial completion for
![]() $\mathsf{Eq}$
adds, in particular, interpretations of the problematic data elements of the form
$\mathsf{Eq}$
adds, in particular, interpretations of the problematic data elements of the form
![]() $\mathsf{map_{Eq}\,h\,k\,Refl}$
from Example 2, even though these may not themselves be of the form
$\mathsf{map_{Eq}\,h\,k\,Refl}$
from Example 2, even though these may not themselves be of the form
![]() $\mathsf{Refl}$
. All of these elements are ghost elements for
$\mathsf{Refl}$
. All of these elements are ghost elements for
![]() $\mathsf{Eq}$
. Similarly, we see that the functorial interpretation of
$\mathsf{Eq}$
. Similarly, we see that the functorial interpretation of
![]() $\mathsf{Seq}$
contains not just interpretations of those data elements representable by its syntax, but also interpretations of all data elements of the form
$\mathsf{Seq}$
contains not just interpretations of those data elements representable by its syntax, but also interpretations of all data elements of the form
![]() $\mathsf{map_{Seq}\,f\,s}$
for all types
$\mathsf{map_{Seq}\,f\,s}$
for all types
![]() $\mathsf{t_1}$
and
$\mathsf{t_1}$
and
![]() $\mathsf{t_2}$
, all functions
$\mathsf{t_2}$
, all functions
![]() $\mathsf{f :: t_1 \to t_2}$
definable in the language, and all
$\mathsf{f :: t_1 \to t_2}$
definable in the language, and all
![]() $\mathsf{s :: Seq\,t_1}$
, as well as interpretations of all data elements of the form
$\mathsf{s :: Seq\,t_1}$
, as well as interpretations of all data elements of the form
![]() $\mathsf{map_{Seq}\,g\,s'}$
for each appropriately typed function
$\mathsf{map_{Seq}\,g\,s'}$
for each appropriately typed function
![]() $\mathsf{g}$
and each element
$\mathsf{g}$
and each element
![]() $\mathsf{s'}$
already added to the data type, and so on. Functorial completion for
$\mathsf{s'}$
already added to the data type, and so on. Functorial completion for
![]() $\mathsf{Seq}$
adds, in particular, interpretations of the problematic data elements of the form
$\mathsf{Seq}$
adds, in particular, interpretations of the problematic data elements of the form
![]() $\mathsf{map_{Seq}\,g\,(Pair\,t_1\,t_2)}$
from Section 3.1, even though these may not themselves be of the form
$\mathsf{map_{Seq}\,g\,(Pair\,t_1\,t_2)}$
from Section 3.1, even though these may not themselves be of the form
![]() $\mathsf{Pair\,t_3\,t_4}$
for any terms
$\mathsf{Pair\,t_3\,t_4}$
for any terms
![]() $\mathsf{t_3}$
and
$\mathsf{t_3}$
and
![]() $\mathsf{t_4}$
. All of these elements are ghost elements for
$\mathsf{t_4}$
. All of these elements are ghost elements for
![]() $\mathsf{Seq}$
. Importantly, functorial completion adds no ghost data elements to the interpretations of GADTs that are ADTs or other nested types.
$\mathsf{Seq}$
. Importantly, functorial completion adds no ghost data elements to the interpretations of GADTs that are ADTs or other nested types.
We will now make the above precise, by showing formally that the functorial completion of a proper GADT necessarily contains more data elements than those representable in the GADT’s syntax because it adds ghost elements to the GADT’s interpretation. When interpreted as their functorial completions, GADTs can, like ADTs, be modeled as fixpoints of higher-order functors. Syntactically, higher-orderness is essential: since the type arguments to the GADT being defined are not necessarily uniform across all of its instances in the types of its data constructors, GADTs cannot be seen as first-order fixpoints the way ADTs can. Semantically, (higher-order) functors are essential: as in the standard semantics for ADTs, functoriality guarantees the existence of the (higher-order) fixpoints being computed (nLab authors Reference nLab2019).
To illustrate the process of computing the functorial completion of a proper GADT, consider again the GADT
![]() $\mathsf{Seq}$
. Because its type argument varies in the instances of
$\mathsf{Seq}$
. Because its type argument varies in the instances of
![]() $\mathsf{Seq}$
appearing in the types of its data constructor
$\mathsf{Seq}$
appearing in the types of its data constructor
![]() $\mathsf{Pair}$
,
$\mathsf{Pair}$
,
![]() $\mathsf{Seq}$
cannot be modeled as the fixpoint of any first-order functor. As shown in (Johann and Polonsky Reference Johann and Polonsky2019), it can, however, be modeled as a solution to the higher-order fixpoint equation
$\mathsf{Seq}$
cannot be modeled as the fixpoint of any first-order functor. As shown in (Johann and Polonsky Reference Johann and Polonsky2019), it can, however, be modeled as a solution to the higher-order fixpoint equation
where
![]() $Lan_K \,F$
is the left Kan extension of the functor
$Lan_K \,F$
is the left Kan extension of the functor
![]() $F$
along the functor
$F$
along the functor
![]() $K$
. In general, the left Kan extension
$K$
. In general, the left Kan extension
![]() $Lan_K \,F : \mathscr{E} \to \mathscr{D}$
of
$Lan_K \,F : \mathscr{E} \to \mathscr{D}$
of
![]() $F : \mathscr{C} \to \mathscr{D}$
along
$F : \mathscr{C} \to \mathscr{D}$
along
![]() $K : \mathscr{C} \to \mathscr{E}$
is the best functorial approximation to
$K : \mathscr{C} \to \mathscr{E}$
is the best functorial approximation to
![]() $F$
that factors through
$F$
that factors through
![]() $K$
. Intuitively, “best functorial approximation” means that
$K$
. Intuitively, “best functorial approximation” means that
![]() $Lan_K \,F$
is the smallest functor that both extends the image of
$Lan_K \,F$
is the smallest functor that both extends the image of
![]() $K$
to
$K$
to
![]() $\mathscr{D}$
and agrees with
$\mathscr{D}$
and agrees with
![]() $F$
on
$F$
on
![]() $\mathscr{C}$
, in the sense that, for any other such functor
$\mathscr{C}$
, in the sense that, for any other such functor
![]() $G$
, there is a morphism of functors (i.e., a natural transformation) from
$G$
, there is a morphism of functors (i.e., a natural transformation) from
![]() $Lan_K \,F$
to
$Lan_K \,F$
to
![]() $G$
. Formally, this is captured by the following definition (MacLane Reference MacLane1971):
$G$
. Formally, this is captured by the following definition (MacLane Reference MacLane1971):
Definition 3.
If
![]() $F : \mathscr{C} \to \mathscr{D}$
and
$F : \mathscr{C} \to \mathscr{D}$
and
![]() $K : \mathscr{C} \to \mathscr{E}$
are functors, then the left Kan extension of
$K : \mathscr{C} \to \mathscr{E}$
are functors, then the left Kan extension of
![]() $F$
along
$F$
along
![]() $K$
is a functor
$K$
is a functor
![]() $\mathit{Lan}_K\,F : \mathscr{E} \to \mathscr{D}$
together with a natural transformation
$\mathit{Lan}_K\,F : \mathscr{E} \to \mathscr{D}$
together with a natural transformation
![]() $\eta : F \to (\mathit{Lan}_K\,F) \circ K$
such that, for every functor
$\eta : F \to (\mathit{Lan}_K\,F) \circ K$
such that, for every functor
![]() $G : \mathscr{E} \to \mathscr{D}$
and natural transformation
$G : \mathscr{E} \to \mathscr{D}$
and natural transformation
![]() $\gamma : F \to G \circ K$
, there exists a unique natural transformation
$\gamma : F \to G \circ K$
, there exists a unique natural transformation
![]() $\delta : \mathit{Lan}_K\,F \to G$
such that
$\delta : \mathit{Lan}_K\,F \to G$
such that
![]() $(\delta K) \circ \eta = \gamma$
. This is depicted in the diagram
$(\delta K) \circ \eta = \gamma$
. This is depicted in the diagram

To represent GADTs as fixpoints in a setting in which types are interpreted as sets, a calculus must support a primitive construct
![]() $\mathsf{Lan}$
in such a way that the type constructor
$\mathsf{Lan}$
in such a way that the type constructor
![]() $\mathsf{Lan_{\overline{K}}\,F}$
is the syntactic reflection of the left Kan extension
$\mathsf{Lan_{\overline{K}}\,F}$
is the syntactic reflection of the left Kan extension
![]() $\mathsf{Lan}_K \,F$
of the functor
$\mathsf{Lan}_K \,F$
of the functor
![]() $F$
interpreting
$F$
interpreting
![]() $\mathsf{F}$
along the functor
$\mathsf{F}$
along the functor
![]() $K$
interpreting
$K$
interpreting
![]() $\overline{\textsf{K}}$
. If
$\overline{\textsf{K}}$
. If
![]() $\textsf{F}$
and the
$\textsf{F}$
and the
![]() $n$
components of
$n$
components of
![]() $\overline{\textsf{K}}$
all have type signature
$\overline{\textsf{K}}$
all have type signature
![]() $*^{k}\to *$
, then
$*^{k}\to *$
, then
![]() $\textsf{Lan}_{\overline{\textsf{K}}}\,{\textsf{F}}$
has type signature
$\textsf{Lan}_{\overline{\textsf{K}}}\,{\textsf{F}}$
has type signature
![]() $*^{n}\to *$
. It also comes together with a term
$*^{n}\to *$
. It also comes together with a term
![]() $\textsf{eta} :: \forall \textsf{b}. \ \textsf{F}\,\overline{\textsf{b}} \to \textsf{Lan}_{\overline{\textsf{K}}} \, \textsf{F}\, \overline{\textsf{K} \,\overline{\textsf{b}}}$
and the following rule: Given a type expression
$\textsf{eta} :: \forall \textsf{b}. \ \textsf{F}\,\overline{\textsf{b}} \to \textsf{Lan}_{\overline{\textsf{K}}} \, \textsf{F}\, \overline{\textsf{K} \,\overline{\textsf{b}}}$
and the following rule: Given a type expression
![]() $\textsf{E}\, \overline{\textsf{a}}$
, whose
$\textsf{E}\, \overline{\textsf{a}}$
, whose
![]() $n$
free type variables are the components of
$n$
free type variables are the components of
![]() $\overline{\textsf{a}}$
, and a term
$\overline{\textsf{a}}$
, and a term
![]() $\textsf{u} :: \forall \overline{\textsf{b}}.\ \textsf{F}\,\overline{\textsf{b}} \to \textsf{E}\, \overline{\textsf{K} \,\overline{\textsf{b}}}$
, there is a unique term
$\textsf{u} :: \forall \overline{\textsf{b}}.\ \textsf{F}\,\overline{\textsf{b}} \to \textsf{E}\, \overline{\textsf{K} \,\overline{\textsf{b}}}$
, there is a unique term
![]() $\textsf{t} :: \forall \overline{\textsf{a}}.\ \textsf{Lan}_{\overline{\textsf{K}}}\,\textsf{F}\,\overline{\textsf{a}} \to \textsf{E}\,\overline{\textsf{a}}$
such that
$\textsf{t} :: \forall \overline{\textsf{a}}.\ \textsf{Lan}_{\overline{\textsf{K}}}\,\textsf{F}\,\overline{\textsf{a}} \to \textsf{E}\,\overline{\textsf{a}}$
such that
![]() $\textsf{t} \circ \textsf{eta} = \textsf{u}$
. For our purposes, the categories
$\textsf{t} \circ \textsf{eta} = \textsf{u}$
. For our purposes, the categories
![]() $\mathscr{C}$
,
$\mathscr{C}$
,
![]() $\mathscr{D}$
, and
$\mathscr{D}$
, and
![]() $\mathscr{E}$
must all be of the form
$\mathscr{E}$
must all be of the form
![]() $\mathit{Set}^m$
for some
$\mathit{Set}^m$
for some
![]() $m$
, and the functors
$m$
, and the functors
![]() $F$
and
$F$
and
![]() $K$
must be finitely accessible. This ensures that the left Kan extensions
$K$
must be finitely accessible. This ensures that the left Kan extensions
![]() $\mathsf{Lan}_K \,F$
all exist, since each category
$\mathsf{Lan}_K \,F$
all exist, since each category
![]() $\mathit{Set}^m$
is locally finitely presentable (see (Johann and Polonsky Reference Johann and Polonsky2019) for a detailed account). Using
$\mathit{Set}^m$
is locally finitely presentable (see (Johann and Polonsky Reference Johann and Polonsky2019) for a detailed account). Using
![]() $\mathsf{Lan}$
we can then rewrite the type of a constructor
$\mathsf{Lan}$
we can then rewrite the type of a constructor
![]() $\mathsf{C :: F\, a \to G\,(K\,a)}$
as
$\mathsf{C :: F\, a \to G\,(K\,a)}$
as
![]() $\mathsf{C :: (Lan_K\,F)\,a \to G\,a}$
since, by Definition 3, morphisms (i.e., natural transformations) from
$\mathsf{C :: (Lan_K\,F)\,a \to G\,a}$
since, by Definition 3, morphisms (i.e., natural transformations) from
![]() $F$
to
$F$
to
![]() $G \circ K$
are in one-to-one correspondence with those from
$G \circ K$
are in one-to-one correspondence with those from
![]() $\mathit{Lan}_K\,F$
to
$\mathit{Lan}_K\,F$
to
![]() $G$
. That is, writing
$G$
. That is, writing
![]() $F \Rightarrow G$
for the set of natural transformations from a functor
$F \Rightarrow G$
for the set of natural transformations from a functor
![]() $F$
to a functor
$F$
to a functor
![]() $G$
, we have
$G$
, we have
The calculus must also support a primitive type constructor
![]() $\mathsf{\mu }$
that is the syntactic reflection of the (now higher-order) fixpoint operator on
$\mathsf{\mu }$
that is the syntactic reflection of the (now higher-order) fixpoint operator on
![]() $\mathit{Set}^{\mathit{Set}}$
. Using
$\mathit{Set}^{\mathit{Set}}$
. Using
![]() $\mu$
and
$\mu$
and
![]() $\mathsf{Lan}$
we can then represent a GADT as a higher-order fixpoint. For example, we can represent the GADT
$\mathsf{Lan}$
we can then represent a GADT as a higher-order fixpoint. For example, we can represent the GADT
![]() $\mathsf{Seq}$
as
$\mathsf{Seq}$
as
The fact that
![]() $Lan_K\,F$
is the best functorial approximation to
$Lan_K\,F$
is the best functorial approximation to
![]() $F$
factoring through
$F$
factoring through
![]() $K$
means that the type constructor
$K$
means that the type constructor
![]() $\mathsf{Lan_K\,F}$
computes the smallest collection of data that is generated by the corresponding GADT data constructor’s syntax and also supports a map function. Such a fixpoint representation of any GADT thus comprises the smallest data type that both includes the data specified by that GADT’s syntax and also supports a map function. When viewed as fixpoints, then, proper GADTs are underspecified by their syntax.
$\mathsf{Lan_K\,F}$
computes the smallest collection of data that is generated by the corresponding GADT data constructor’s syntax and also supports a map function. Such a fixpoint representation of any GADT thus comprises the smallest data type that both includes the data specified by that GADT’s syntax and also supports a map function. When viewed as fixpoints, then, proper GADTs are underspecified by their syntax.
We can use Definition 3 to make precise the intuition that functorial completion adds in new elements to interpretations of proper GADTs. This will be shown explicitly in the next example. Despite its simplicity, the GADT defined in (10) serves as an informative case study highlighting the difference between simply interpreting a proper GADT’s syntax and interpreting a proper GADT’s syntax as a functor – even if we are content to consider only the data elements it contains and ignore whether or not it supports a map function.
Example 4.
Syntactically, the GADT
![]() $\mathsf{G}$
defined by
$\mathsf{G}$
defined by
comprises a single data element, namely
![]() $\mathsf{C :: G \, 1}$
. As the definition of
$\mathsf{C :: G \, 1}$
. As the definition of
![]() $\mathsf{G}$
makes clear,
$\mathsf{G}$
makes clear,
![]() $\mathsf{G}$
’s effect is simply to test its argument for equality against the unit type
$\mathsf{G}$
’s effect is simply to test its argument for equality against the unit type
![]() $\mathsf{1}$
. To compute the interpretation of
$\mathsf{1}$
. To compute the interpretation of
![]() $\mathsf{G}$
’s fixpoint representation we first note that the type of
$\mathsf{G}$
’s fixpoint representation we first note that the type of
![]() $\mathsf{G}$
’s solitary constructor
$\mathsf{G}$
’s solitary constructor
![]() $\mathsf{C :: G\,1}$
is equivalently expressed as
$\mathsf{C :: G\,1}$
is equivalently expressed as
![]() $\mathsf{C :: 1 \to G\,1}$
or, using (9), as
$\mathsf{C :: 1 \to G\,1}$
or, using (9), as
![]() $\mathsf{C :: (Lan_{\lambda u. 1}\,\lambda u. 1)\,a \to G\, a}$
, where
$\mathsf{C :: (Lan_{\lambda u. 1}\,\lambda u. 1)\,a \to G\, a}$
, where
![]() $\mathsf{\lambda u. 1}$
is the syntactic reflection of the constantly
$\mathsf{\lambda u. 1}$
is the syntactic reflection of the constantly
![]() $1$
-valued functor from the category
$1$
-valued functor from the category
![]() $\mathit{Set}^0$
with a single object to
$\mathit{Set}^0$
with a single object to
![]() $\mathit{Set}$
. We can therefore represent
$\mathit{Set}$
. We can therefore represent
![]() $\mathsf{G}$
as
$\mathsf{G}$
as
The interpretation of
![]() $\mathsf{G}$
is obtained by computing the fixpoint of the interpretation of the body
$\mathsf{G}$
is obtained by computing the fixpoint of the interpretation of the body
![]() $\mathsf{\lambda b. (Lan_{\lambda u. 1} \,\lambda u. 1)\,b}$
of the syntactic fixpoint
$\mathsf{\lambda b. (Lan_{\lambda u. 1} \,\lambda u. 1)\,b}$
of the syntactic fixpoint
![]() $\mathsf{\mu \phi . \lambda b. (Lan_{\lambda u. 1} \,\lambda u. 1)\,b}$
and applying the result to
$\mathsf{\mu \phi . \lambda b. (Lan_{\lambda u. 1} \,\lambda u. 1)\,b}$
and applying the result to
![]() $\mathsf{a}$
. But since the recursion variable
$\mathsf{a}$
. But since the recursion variable
![]() $\mathsf{\phi }$
does not appear in this body, the interpretation of the fixpoint is just the interpretation of the body itself. The interpretation of
$\mathsf{\phi }$
does not appear in this body, the interpretation of the fixpoint is just the interpretation of the body itself. The interpretation of
![]() $\mathsf{G\,a}$
is therefore
$\mathsf{G\,a}$
is therefore
![]() $(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\, A$
, where
$(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\, A$
, where
![]() $A$
interprets
$A$
interprets
![]() $\mathsf{a}$
. It turns out, however, that, for any set
$\mathsf{a}$
. It turns out, however, that, for any set
![]() $A$
,
$A$
,
![]() $(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A$
is, in fact, exactly
$(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A$
is, in fact, exactly
![]() $A$
. Indeed, Proposition 7.1 of (Bush et al., Reference Bush, Leeming and Walters2003) gives that
$A$
. Indeed, Proposition 7.1 of (Bush et al., Reference Bush, Leeming and Walters2003) gives that
![]() $(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A$
can be computed as
$(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A$
can be computed as
where
![]() $U$
is the unique object of
$U$
is the unique object of
![]() $\mathit{Set}^0$
,
$\mathit{Set}^0$
,
![]() $*$
is the unique element of the singleton set
$*$
is the unique element of the singleton set
![]() $1$
, and
$1$
, and
![]() $\sim$
is the smallest equivalence relation such that
$\sim$
is the smallest equivalence relation such that
![]() $(U,f, *)$
and
$(U,f, *)$
and
![]() $(U,f',*)$
are related if
$(U,f',*)$
are related if

commutes, i.e., if
![]() $f = f'$
. Since the relation generating
$f = f'$
. Since the relation generating
![]() $\sim$
is already an equivalence relation, we have that
$\sim$
is already an equivalence relation, we have that
![]() $(U,f,*) \sim (U,f', *)$
iff
$(U,f,*) \sim (U,f', *)$
iff
![]() $f = f'$
. Thus, up to isomorphism,
$f = f'$
. Thus, up to isomorphism,
![]() $(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A = \{ f : 1 \to A\}$
, i.e.,
$(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A = \{ f : 1 \to A\}$
, i.e.,
![]() $(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A = A$
.
$(\mathit{Lan}_{\lambda u. 1} \lambda u. 1)\,A = A$
.
Notice that this is different from what we expect just by looking at
![]() $\mathsf{G}$
’s syntax. Indeed, we expect exactly one data element at instance
$\mathsf{G}$
’s syntax. Indeed, we expect exactly one data element at instance
![]() $\mathsf{G\,1}$
and no elements at any other instances. However, the interpretation of the fixpoint representation of
$\mathsf{G\,1}$
and no elements at any other instances. However, the interpretation of the fixpoint representation of
![]() $\mathsf{G}$
has data elements at every instance other than
$\mathsf{G}$
has data elements at every instance other than
![]() $\mathsf{G\,0}$
. These additional data elements can be obtained by reflecting back into syntax the elements
$\mathsf{G\,0}$
. These additional data elements can be obtained by reflecting back into syntax the elements
![]() $\mathit{map}_G\,f_a\,c \in G\,A$
resulting from applying the functorial action
$\mathit{map}_G\,f_a\,c \in G\,A$
resulting from applying the functorial action
![]() $\mathit{map}_G$
of
$\mathit{map}_G$
of
![]() $\mathsf{G}$
’s interpretation
$\mathsf{G}$
’s interpretation
![]() $G$
to the functions
$G$
to the functions
![]() $f_a : 1 \to A$
determined by the elements
$f_a : 1 \to A$
determined by the elements
![]() $a$
of
$a$
of
![]() $A \not = \emptyset$
and the interpretation
$A \not = \emptyset$
and the interpretation
![]() $c$
of
$c$
of
![]() $\mathsf{C}$
.
$\mathsf{C}$
.
More fundamentally, we have
Example 5.
Syntactically, the GADT
![]() $\mathsf{Eq}$
defined in (8) comprises the data elements
$\mathsf{Eq}$
defined in (8) comprises the data elements
![]() $\mathsf{Refl :: Eq \, c\, c}$
for each type
$\mathsf{Refl :: Eq \, c\, c}$
for each type
![]() $\mathsf{c}$
, and no others. In other words,
$\mathsf{c}$
, and no others. In other words,
![]() $\mathsf{Eq}$
’s effect is to test the equality of its two arguments. To compute the interpretation of the binary GADT
$\mathsf{Eq}$
’s effect is to test the equality of its two arguments. To compute the interpretation of the binary GADT
![]() $\mathsf{Eq}$
’s fixpoint representation, we first note that
$\mathsf{Eq}$
’s fixpoint representation, we first note that
![]() $\mathsf{Eq}$
’s sole constructor
$\mathsf{Eq}$
’s sole constructor
![]() $\mathsf{Refl :: Eq \,c \, c}$
is equivalently expressed as
$\mathsf{Refl :: Eq \,c \, c}$
is equivalently expressed as
![]() $\mathsf{Refl :: 1 \to Eq\, c\, c}$
or, using (9), as
$\mathsf{Refl :: 1 \to Eq\, c\, c}$
or, using (9), as
![]() $\mathsf{Refl :: (Lan_{\lambda c. (c,c)}\,\lambda c. 1)\,a\,b) \to Eq\, a\, b}$
, where
$\mathsf{Refl :: (Lan_{\lambda c. (c,c)}\,\lambda c. 1)\,a\,b) \to Eq\, a\, b}$
, where
![]() $\mathsf{\lambda c. 1}$
is the syntactic reflection of the constantly
$\mathsf{\lambda c. 1}$
is the syntactic reflection of the constantly
![]() $1$
-valued functor from the category
$1$
-valued functor from the category
![]() $\mathit{Set}$
to itself, and
$\mathit{Set}$
to itself, and
![]() $\mathsf{\lambda c. (c,c)}$
is that of the diagonal functor from
$\mathsf{\lambda c. (c,c)}$
is that of the diagonal functor from
![]() $\mathit{Set}$
to
$\mathit{Set}$
to
![]() $\mathit{Set}^2$
mapping every set
$\mathit{Set}^2$
mapping every set
![]() $C$
to the pair
$C$
to the pair
![]() $(C,C)$
. We can therefore represent
$(C,C)$
. We can therefore represent
![]() $\mathsf{Eq}$
as
$\mathsf{Eq}$
as
The interpretation of
![]() $\mathsf{Eq}$
is obtained by computing the fixpoint of the interpretation of the body
$\mathsf{Eq}$
is obtained by computing the fixpoint of the interpretation of the body
![]() $\mathsf{\lambda d \,e. (Lan_{\lambda c. (c,c)} \,\lambda c. 1)\,d\,e}$
of the syntactic fixpoint
$\mathsf{\lambda d \,e. (Lan_{\lambda c. (c,c)} \,\lambda c. 1)\,d\,e}$
of the syntactic fixpoint
![]() $\mathsf{\mu \phi . \lambda d\,e. (Lan_{\lambda c. (c,c)} \,\lambda c. 1)\,d\,e}$
and applying the result to
$\mathsf{\mu \phi . \lambda d\,e. (Lan_{\lambda c. (c,c)} \,\lambda c. 1)\,d\,e}$
and applying the result to
![]() $\mathsf{a}$
and
$\mathsf{a}$
and
![]() $\mathsf{b}$
. But since the recursion variable
$\mathsf{b}$
. But since the recursion variable
![]() $\mathsf{\phi }$
does not appear in this body, the interpretation of the fixpoint is just the interpretation of the body itself. The interpretation of
$\mathsf{\phi }$
does not appear in this body, the interpretation of the fixpoint is just the interpretation of the body itself. The interpretation of
![]() $\mathsf{Eq\,a\,b}$
is therefore
$\mathsf{Eq\,a\,b}$
is therefore
![]() $(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
, where
$(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
, where
![]() $A$
and
$A$
and
![]() $B$
interpret
$B$
interpret
![]() $\mathsf{a}$
and
$\mathsf{a}$
and
![]() $\mathsf{b}$
, respectively. It turns out, however, that, for any sets
$\mathsf{b}$
, respectively. It turns out, however, that, for any sets
![]() $A$
and
$A$
and
![]() $B$
,
$B$
,
![]() $(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
is, in fact, the singleton set
$(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
is, in fact, the singleton set
![]() $1$
. Indeed, Proposition 7.1 of (Bush et al. Reference Bush, Leeming and Walters2003) gives that
$1$
. Indeed, Proposition 7.1 of (Bush et al. Reference Bush, Leeming and Walters2003) gives that
![]() $(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
can be computed as
$(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B)$
can be computed as
where
![]() $\sim$
is the smallest equivalence relation such that
$\sim$
is the smallest equivalence relation such that
![]() $(C,f,g,*)$
and
$(C,f,g,*)$
and
![]() $(C',f',g',*)$
are related if there exists
$(C',f',g',*)$
are related if there exists
![]() $h:C\to C'$
such that
$h:C\to C'$
such that

commutes. We can see that any element
![]() $(C,f,g,*)$
is related to
$(C,f,g,*)$
is related to
![]() $(A\times B, \pi _1, \pi _2,*)$
, where
$(A\times B, \pi _1, \pi _2,*)$
, where
![]() $\pi _1 : A \times B \to A$
and
$\pi _1 : A \times B \to A$
and
![]() $\pi _2 : A \times B \to B$
are the first and second projections out of
$\pi _2 : A \times B \to B$
are the first and second projections out of
![]() $A\times B$
, respectively. In other words,
$A\times B$
, respectively. In other words,
![]() $\sim$
relates any element with any other. Thus, up to isomorphism,
$\sim$
relates any element with any other. Thus, up to isomorphism,
![]() $(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B) = 1$
.
$(\mathit{Lan}_{\lambda c. (c,c)} \lambda c. 1)\,(A,B) = 1$
.
Notice that this is different from what we expect just looking at
![]() $\mathsf{Eq}$
’s syntax: We expect exactly one data element at instance
$\mathsf{Eq}$
’s syntax: We expect exactly one data element at instance
![]() $\mathsf{Eq\,a\,a}$
for each type
$\mathsf{Eq\,a\,a}$
for each type
![]() $\mathsf{a}$
and no elements at any other instances. However, the interpretation of the fixpoint representation of
$\mathsf{a}$
and no elements at any other instances. However, the interpretation of the fixpoint representation of
![]() $\mathsf{Eq\,a\, b}$
has data elements at every instance. These additional data elements can be obtained by reflecting back into syntax the elements
$\mathsf{Eq\,a\, b}$
has data elements at every instance. These additional data elements can be obtained by reflecting back into syntax the elements
![]() $\mathit{map}_{Eq}\,(\pi _1,\pi _2)\,r\in Eq(A,B)$
resulting from applying the functorial action
$\mathit{map}_{Eq}\,(\pi _1,\pi _2)\,r\in Eq(A,B)$
resulting from applying the functorial action
![]() $\mathit{map}_{\mathit{Eq}}$
of
$\mathit{map}_{\mathit{Eq}}$
of
![]() $\mathsf{Eq}$
’s interpretation
$\mathsf{Eq}$
’s interpretation
![]() $\mathit{Eq}$
to
$\mathit{Eq}$
to
![]() $\pi _1$
,
$\pi _1$
,
![]() $\pi _2$
, and the interpretation
$\pi _2$
, and the interpretation
![]() $r$
of
$r$
of
![]() $\mathsf{Refl}$
in
$\mathsf{Refl}$
in
![]() $\mathit{Eq}(A\times B, A\times B)$
.
$\mathit{Eq}(A\times B, A\times B)$
.
4.1 Functorial interpretations in
 $\mathit{Set}$
are insufficient
$\mathit{Set}$
are insufficient
We have now seen that even though the functorial completions of
![]() $\mathsf{G}$
and
$\mathsf{G}$
and
![]() $\mathsf{Eq}$
give the smallest extending functor interpreting GADTs, they must still introduce ghost elements. And since all proper GADTs can be written in terms of
$\mathsf{Eq}$
give the smallest extending functor interpreting GADTs, they must still introduce ghost elements. And since all proper GADTs can be written in terms of
![]() $\mathsf{Eq}$
, the same is true for them. But why should a programmer accept elements in the interpretation of a proper GADT that are not reachable in syntax? Forced to choose, a programmer would likely find the idea that a proper GADT contains data not specified by its syntax more than a little disturbing. What, they might ask, should a data type contain other than data that are constructed using its data constructors? That is, why should a proper GADT’s interpretation contain ghost elements that are not specified by its syntax, and are only accessible via applications of its interpretation’s functorial action?
$\mathsf{Eq}$
, the same is true for them. But why should a programmer accept elements in the interpretation of a proper GADT that are not reachable in syntax? Forced to choose, a programmer would likely find the idea that a proper GADT contains data not specified by its syntax more than a little disturbing. What, they might ask, should a data type contain other than data that are constructed using its data constructors? That is, why should a proper GADT’s interpretation contain ghost elements that are not specified by its syntax, and are only accessible via applications of its interpretation’s functorial action?
From a semanticist’s point of view, on the other hand, functorial completions of GADTs are entirely reasonable. Indeed, a semanticist would likely find the nonfunctorial nature of a GADT’s syntax unnerving at best. After all, they would likely argue, if a GADT is supposed to be a data type, then the data in it shouldn’t change or become ill-typed just because a function is mapped over it. The fact that this happens to GADTs when regarded just as their syntax actually highlights how GADTs do not generalize the essential, container-ish nature of ADTs at all. A semanticist might therefore conclude that GADTs are, at the very least, seriously misnamed.
Note, however, that even if we do accept ghost elements in the interpretation of GADTs, they still don’t behave as expected. Indeed, as we show in Section 5, a language interpreting GADTs as their functorial completions cannot have parametric models (Reynolds Reference Reynolds1983), as we would expect them to do. This means that languages with GADTs do not necessarily enjoy consequences of parametricity such as representation independence (Ahmed et al. Reference Ahmed, Dreyer and Rossberg2009; Dreyer et al. Reference Dreyer, Neis and Birkedal2012), equivalences between programs (Hur and Dreyer Reference Hur and Dreyer2011), deep induction principles (Johann and Ghiorzi Reference Johann and Ghiorzi2022; Johann and Polonsky Reference Johann and Polonsky2020), and useful (“free”) theorems about programs derived from their types alone (Wadler Reference Wadler1989).
5. Functorial Completion Does Not Support Parametric Semantics
Relational parametricity encodes a powerful notion of type uniformity, or representation independence, for data types in functional languages. It formalizes the intuition that a polymorphic program must act uniformly on all of its possible type instantiations by requiring that every such program preserves all relations between pairs of types at which it is instantiated. Parametricity was originally put forth by Reynolds (Reynolds Reference Reynolds1983) for System F. It was later popularized as Wadler’s “theorems for free” (Wadler Reference Wadler1989), so called because it can deduce properties of programs solely from their types, i.e., with no knowledge whatsoever of the text of the programs involved. Most of Wadler’s free theorems are consequences of naturality for polymorphic list-processing functions. However, parametricity can also derive results that go beyond just naturality, such as inhabitation results. It can also be used to prove the equivalence of Church encodings and fixpoint representations of ADTs and nested types by validating shortcut fusion and other program equivalences for them (Johann Reference Johann2002; Wadler Reference Wadler1989).
To show that interpreting GADTs as their functorial completions cannot lead to a parametric semantics, and thus that the semantics they do lead to are unsatisfactory for reasoning about programs involving GADTs, we will need to interpret data types not just in
![]() $\mathit{Set}$
, but in a suitable category of relations as well. The following definition is standard:
$\mathit{Set}$
, but in a suitable category of relations as well. The following definition is standard:
Definition 6.
The category
![]() $\mathit{Rel}$
has:
$\mathit{Rel}$
has:
-
• objects: A relation is a triple
 $(A,B,R)$
, where
$(A,B,R)$
, where
 $R$
is a subset of
$R$
is a subset of
 $A \times B$
.
$A \times B$
. -
• morphisms: A morphism from
 $(A,B,R)$
to
$(A,B,R)$
to
 $(A',B',R')$
is a pair
$(A',B',R')$
is a pair
 $(f : A \to A',g : B \to B')$
of functions in
$(f : A \to A',g : B \to B')$
of functions in
 $\mathit{Set}$
such that
$\mathit{Set}$
such that
 $(f a,g\,b) \in R'$
if
$(f a,g\,b) \in R'$
if
 $(a,b) \in R$
.
$(a,b) \in R$
. -
• identities: The identity morphism on
 $(A,B,R)$
is the pair
$(A,B,R)$
is the pair
 $(\mathit{id}_A : A \to A, \mathit{id}_B : B \to B)$
.
$(\mathit{id}_A : A \to A, \mathit{id}_B : B \to B)$
. -
• composition: Composition is the componentwise composition in
 $\mathit{Set}$
. That is,
$\mathit{Set}$
. That is,
 $(g_1,g_2) \circ (f_1,f_2) = (g_1 \circ f_1, g_2 \circ f_2)$
, where the composition being defined on the left-hand side is in
$(g_1,g_2) \circ (f_1,f_2) = (g_1 \circ f_1, g_2 \circ f_2)$
, where the composition being defined on the left-hand side is in
 $\mathit{Rel}$
, and the two componentwise compositions on the right-hand side are in
$\mathit{Rel}$
, and the two componentwise compositions on the right-hand side are in
 $\mathit{Set}$
.
$\mathit{Set}$
.
We write
![]() $R \in \mathit{Rel}\,(A,B)$
for
$R \in \mathit{Rel}\,(A,B)$
for
![]() $(A,B,R) \in \mathit{Rel}$
. If
$(A,B,R) \in \mathit{Rel}$
. If
![]() $R \in \mathit{Rel}\,(A,B)$
then we write
$R \in \mathit{Rel}\,(A,B)$
then we write
![]() $\pi _1 R$
and
$\pi _1 R$
and
![]() $\pi _2 R$
for the domain
$\pi _2 R$
for the domain
![]() $A$
and codomain
$A$
and codomain
![]() $B$
of
$B$
of
![]() $R$
, respectively. We write
$R$
, respectively. We write
![]() $\mathit{I}_A = (A,A,\{(x,x)\,|\, x \in A\})$
for the equality relation on the set
$\mathit{I}_A = (A,A,\{(x,x)\,|\, x \in A\})$
for the equality relation on the set
![]() $A$
.
$A$
.
The key idea underlying parametricity is to give each type
![]() $\mathsf{G[a]}$
Footnote 7 with one free variable
$\mathsf{G[a]}$
Footnote 7 with one free variable
![]() $\mathsf{a}$
a set interpretation
$\mathsf{a}$
a set interpretation
![]() $G_0$
taking sets to sets and a relational interpretation
$G_0$
taking sets to sets and a relational interpretation
![]() $G_1$
taking relations
$G_1$
taking relations
![]() $R \in \mathit{Rel}\,(A,B)$
to relations
$R \in \mathit{Rel}\,(A,B)$
to relations
![]() $G_1 \,R \in \mathit{Rel}\,(G_0 \,A, G_0 \,B)$
, and to interpret each term
$G_1 \,R \in \mathit{Rel}\,(G_0 \,A, G_0 \,B)$
, and to interpret each term
![]() $\mathsf{t\,(a,x) :: G[a]}$
with one free term variable
$\mathsf{t\,(a,x) :: G[a]}$
with one free term variable
![]() $\mathsf{x :: F[a]}$
as a function
$\mathsf{x :: F[a]}$
as a function
![]() $t$
associating to each set
$t$
associating to each set
![]() $A$
a morphism
$A$
a morphism
![]() $t \,A : F_0\,A \to G_0\,A$
in
$t \,A : F_0\,A \to G_0\,A$
in
![]() $\mathit{Set}$
. Here,
$\mathit{Set}$
. Here,
![]() $F_0$
is the set interpretation of
$F_0$
is the set interpretation of
![]() $\mathsf{F}$
. These interpretations are given inductively on the structures of
$\mathsf{F}$
. These interpretations are given inductively on the structures of
![]() $\mathsf{G}$
and
$\mathsf{G}$
and
![]() $\mathsf{t}$
in such a way that they imply two fundamental theorems. The first is an Identity Extension Lemma, which states that
$\mathsf{t}$
in such a way that they imply two fundamental theorems. The first is an Identity Extension Lemma, which states that
![]() $G_1\,\mathit{I}_A = \mathit{I}_{G_0 A}$
, and is the essential property that makes a model relationally parametric rather than just induced by a logical relation. The second is an Abstraction Theorem, which states that, for any
$G_1\,\mathit{I}_A = \mathit{I}_{G_0 A}$
, and is the essential property that makes a model relationally parametric rather than just induced by a logical relation. The second is an Abstraction Theorem, which states that, for any
![]() $R \in \mathit{Rel}\,(A, B)$
,
$R \in \mathit{Rel}\,(A, B)$
,
![]() $(t\, A, t\,B)$
is a morphism in
$(t\, A, t\,B)$
is a morphism in
![]() $\mathit{Rel}$
from
$\mathit{Rel}$
from
![]() $(F_0\,A,F_0\,B,F_1\,R)$
to
$(F_0\,A,F_0\,B,F_1\,R)$
to
![]() $(G_0\,A,G_0\,B,G_1\,R)$
. The Identity Extension Lemma is similar to the Abstraction Theorem except that it holds for all elements of a type’s interpretation, not just those that interpret terms. Similar theorems are required for types and terms with any number of free variables. In particular, if
$(G_0\,A,G_0\,B,G_1\,R)$
. The Identity Extension Lemma is similar to the Abstraction Theorem except that it holds for all elements of a type’s interpretation, not just those that interpret terms. Similar theorems are required for types and terms with any number of free variables. In particular, if
![]() $\mathsf{t}$
is closed (i.e., has no free term variables) then
$\mathsf{t}$
is closed (i.e., has no free term variables) then
![]() $t\,A \in G_0\,A$
for all
$t\,A \in G_0\,A$
for all
![]() $A \in \mathit{Set}$
, and
$A \in \mathit{Set}$
, and
![]() $(t\,A, t\,B) \in G_1\,R$
for all
$(t\,A, t\,B) \in G_1\,R$
for all
![]() $A, B \in \mathit{Set}$
and all
$A, B \in \mathit{Set}$
and all
![]() $R\in \mathit{Rel}(A,B)$
.
$R\in \mathit{Rel}(A,B)$
.
Before showing that languages interpreting GADTs as their functorial completions cannot have parametric models, we first show that languages interpreting them as the interpretations of their Church encodings can. The Church encoding of an ADT or nested type (see, e.g., (Geuvers Reference Geuvers2014; Koopman et al. Reference Koopman, Plasmeijer and Jansen2014; Pierce Reference Pierce2002)) represents that data type as a term in the higher-order polymorphic lambda calculus F
![]() $_\omega$
(Barendregt Reference Barendregt1984), an extension of System F whose type expressions include functions from types to types (i.e., type constructors) and whose terms can abstract over types of all kinds. In particular, expressions of any kind can be universally quantified over variables of any kind. This makes it possible to give Church encodings of ADTs and nested types in F
$_\omega$
(Barendregt Reference Barendregt1984), an extension of System F whose type expressions include functions from types to types (i.e., type constructors) and whose terms can abstract over types of all kinds. In particular, expressions of any kind can be universally quantified over variables of any kind. This makes it possible to give Church encodings of ADTs and nested types in F
![]() $_\omega$
that are similar to, e.g., the standard Church encoding of natural numbers in System F. For example, the Church encoding of the type
$_\omega$
that are similar to, e.g., the standard Church encoding of natural numbers in System F. For example, the Church encoding of the type
![]() $\mathsf{List\, a}$
in F
$\mathsf{List\, a}$
in F
![]() $_\omega$
is
$_\omega$
is
and that of
![]() $\mathsf{PTree\, a}$
is
$\mathsf{PTree\, a}$
is
GADTs can be encoded in the same way. For instance, the Church encoding of the type
![]() $\mathsf{Seq\, a}$
is
$\mathsf{Seq\, a}$
is
while that of
![]() $\mathsf{G\, a}$
is
$\mathsf{G\, a}$
is
The fact that interpreting GADTs as the interpretations of their Church encodings does admit parametric models (Atkey Reference Atkey, Cégielski and Durand2012), whereas interpreting them as their functorial completions does not, means that these two interpretations of GADTs cannot possibly be equivalent. Taken together, Examples 7 and 8 will show that they actually behave very differently with respect to parametricity. This contrasts sharply with the fact that both ADTs and nested types have the same parametricity properties regardless of whether they are interpreted as the interpretations of their Church encodings or as their functorial completions. This is yet another way in which the functorial completion semantics for GADTs is unsatisfactory: it specializes in the standard IAS for ADTs, but it doesn’t share the same parametricity properties.
The existence of parametric models that interpret GADTs as the interpretations of their Church encodings follows from, e.g., the existence of the parametric model of
![]() $F_\omega$
constructed in (Atkey Reference Atkey, Cégielski and Durand2012). In that model, types are interpreted “in parallel” in (types corresponding to)
$F_\omega$
constructed in (Atkey Reference Atkey, Cégielski and Durand2012). In that model, types are interpreted “in parallel” in (types corresponding to)
![]() $\mathit{Set}$
and
$\mathit{Set}$
and
![]() $\mathit{Rel}$
in the usual way, including the familiar “cutting down” of the interpretations of
$\mathit{Rel}$
in the usual way, including the familiar “cutting down” of the interpretations of
![]() $\forall$
-types to just those elements that are “parametric” (Reynolds Reference Reynolds1983; Wadler Reference Wadler1989) to ensure that the Identity Extension Lemma holds. If the set interpretation of
$\forall$
-types to just those elements that are “parametric” (Reynolds Reference Reynolds1983; Wadler Reference Wadler1989) to ensure that the Identity Extension Lemma holds. If the set interpretation of
![]() $\mathsf{Eq}$
is the function
$\mathsf{Eq}$
is the function
![]() $\mathit{Eq}$
and if the relational interpretation of a closed type
$\mathit{Eq}$
and if the relational interpretation of a closed type
![]() $\mathsf{a}$
with interpretation
$\mathsf{a}$
with interpretation
![]() $A$
is
$A$
is
![]() $\mathit{I}_A$
as intended, then the parametricity property for a GADT is an inhabitation result saying that the set interpreting any instance of that GADT contains exactly the interpretations of the data elements that can be formed using its data constructors and whose type is that instance. The parametricity property for the Church encoding of a GADT
$\mathit{I}_A$
as intended, then the parametricity property for a GADT is an inhabitation result saying that the set interpreting any instance of that GADT contains exactly the interpretations of the data elements that can be formed using its data constructors and whose type is that instance. The parametricity property for the Church encoding of a GADT
![]() $\mathsf{G}$
gives that
$\mathsf{G}$
gives that
![]() $\mathsf{G\,a}$
is inhabited iff data elements of the instance of
$\mathsf{G\,a}$
is inhabited iff data elements of the instance of
![]() $\mathsf{G}$
at
$\mathsf{G}$
at
![]() $\mathsf{a}$
can be formed using
$\mathsf{a}$
can be formed using
![]() $\mathsf{G}$
’s data constructors. In particular, the parametricity property for the GADT
$\mathsf{G}$
’s data constructors. In particular, the parametricity property for the GADT
![]() $\mathsf{G}$
from (10) gives that
$\mathsf{G}$
from (10) gives that
![]() $\mathsf{G\,a}$
contains a single data element if
$\mathsf{G\,a}$
contains a single data element if
![]() $\mathsf{a}$
is semantically equivalent to
$\mathsf{a}$
is semantically equivalent to
![]() $\mathsf{1}$
and none otherwise. Indeed, we have
$\mathsf{1}$
and none otherwise. Indeed, we have
Example 7.
Let
![]() $\mathsf{t}$
be a closed term of type
$\mathsf{t}$
be a closed term of type
![]() $\mathsf{G\,a}$
for the GADT
$\mathsf{G\,a}$
for the GADT
![]() $\mathsf{G}$
defined in (10), let
$\mathsf{G}$
defined in (10), let
![]() $G = (G_0,G_1)$
be the interpretation of the Church encoding of
$G = (G_0,G_1)$
be the interpretation of the Church encoding of
![]() $\mathsf{G}$
, let
$\mathsf{G}$
, let
![]() $t$
be the interpretation of
$t$
be the interpretation of
![]() $\mathsf{t}$
, and let
$\mathsf{t}$
, and let
![]() $R \in \mathit{Rel}\,(A,B)$
. Then
$R \in \mathit{Rel}\,(A,B)$
. Then
![]() $t\, A \in G_0\,A$
and
$t\, A \in G_0\,A$
and
![]() $t\,B \in G_0\,B$
and, by the Abstraction Theorem (Theorem 3) in (Atkey Reference Atkey, Cégielski and Durand2012),
$t\,B \in G_0\,B$
and, by the Abstraction Theorem (Theorem 3) in (Atkey Reference Atkey, Cégielski and Durand2012),
![]() $t\,A$
and
$t\,A$
and
![]() $t\,B$
must be related in
$t\,B$
must be related in
![]() $G_1\,R$
. However, under the semantics given in (Atkey Reference Atkey, Cégielski and Durand2012), which includes the aforementioned interpretations of
$G_1\,R$
. However, under the semantics given in (Atkey Reference Atkey, Cégielski and Durand2012), which includes the aforementioned interpretations of
![]() $\mathsf{Eq}$
and closed types, the relational interpretation
$\mathsf{Eq}$
and closed types, the relational interpretation
![]() $G_1\,R$
of
$G_1\,R$
of
![]() $\mathsf{G}$
is itself
$\mathsf{G}$
is itself
![]() $\mathit{I}_{G_0 1}$
when
$\mathit{I}_{G_0 1}$
when
![]() $R$
is the relational interpretation
$R$
is the relational interpretation
![]() $\mathit{I}_1$
of
$\mathit{I}_1$
of
![]() $\mathsf{1}$
, and the empty relation whenever
$\mathsf{1}$
, and the empty relation whenever
![]() $R$
differs from
$R$
differs from
![]() $\mathit{I}_1$
. Reflecting back into syntax we deduce that there can be no term in the type that is the Church encoding of
$\mathit{I}_1$
. Reflecting back into syntax we deduce that there can be no term in the type that is the Church encoding of
![]() $\mathsf{G\,a}$
unless
$\mathsf{G\,a}$
unless
![]() $\mathsf{a}$
is semantically equivalent to
$\mathsf{a}$
is semantically equivalent to
![]() $\mathsf{1}$
.
$\mathsf{1}$
.
For functorial completion interpretations of GADTs, the story is completely different. If, as intended, the set interpretation of
![]() $\mathsf{Lan_K\,F}$
is
$\mathsf{Lan_K\,F}$
is
![]() $\mathit{Lan}_K\,F$
, where
$\mathit{Lan}_K\,F$
, where
![]() $K$
is the set interpretation of
$K$
is the set interpretation of
![]() $\mathsf{K}$
and
$\mathsf{K}$
and
![]() $F$
is the set interpretation of
$F$
is the set interpretation of
![]() $\mathsf{F}$
, then the exact same reasoning gives that the relational interpretation of
$\mathsf{F}$
, then the exact same reasoning gives that the relational interpretation of
![]() $\mathsf{Lan_K\,F}$
is
$\mathsf{Lan_K\,F}$
is
![]() $\mathit{Lan}_K\,F$
, where
$\mathit{Lan}_K\,F$
, where
![]() $K$
is the relational interpretation of
$K$
is the relational interpretation of
![]() $\mathsf{K}$
and
$\mathsf{K}$
and
![]() $F$
is the relational interpretation of
$F$
is the relational interpretation of
![]() $\mathsf{F}$
. But under these interpretations, there can be no parametric model. The following counterexample establishes this surprising result.
$\mathsf{F}$
. But under these interpretations, there can be no parametric model. The following counterexample establishes this surprising result.
Example 8.
In any parametric model, we must give both a set interpretation and a relational interpretation for every type as described at the start of this section. In particular, for every GADT
![]() $\mathsf{G}$
we must give an interpretation
$\mathsf{G}$
we must give an interpretation
![]() $G = (G_0,G_1)$
such that, for every relation
$G = (G_0,G_1)$
such that, for every relation
![]() $R \in \mathit{Rel}\,(A, B)$
, we have
$R \in \mathit{Rel}\,(A, B)$
, we have
![]() $G_1\,R \in \mathit{Rel}\,(G_0\,A, G_0\,B)$
. Intuitively, when
$G_1\,R \in \mathit{Rel}\,(G_0\,A, G_0\,B)$
. Intuitively, when
![]() $\mathsf{G}$
is viewed as a fixpoint, its data elements include those given by its functorial completion. Since
$\mathsf{G}$
is viewed as a fixpoint, its data elements include those given by its functorial completion. Since
![]() $G_1$
is a functor, given any relation
$G_1$
is a functor, given any relation
![]() $S \in \mathit{Rel}\,(C, D)$
and any morphism
$S \in \mathit{Rel}\,(C, D)$
and any morphism
![]() $m : S \to R$
,
$m : S \to R$
,
![]() $G_1\, R$
must contain all elements of the form
$G_1\, R$
must contain all elements of the form
![]() $G_1\,m\,x$
for
$G_1\,m\,x$
for
![]() $x \in G_1\,S$
. But the two components
$x \in G_1\,S$
. But the two components
![]() $m_1 : C \to A$
and
$m_1 : C \to A$
and
![]() $m_2 : D \to B$
of
$m_2 : D \to B$
of
![]() $m$
cannot be given independently of one another, since Definition
6 entails that
$m$
cannot be given independently of one another, since Definition
6 entails that
![]() $(m_1\,c, m_2\,d)$
must be in
$(m_1\,c, m_2\,d)$
must be in
![]() $R$
whenever
$R$
whenever
![]() $(c,d)$
is in
$(c,d)$
is in
![]() $S$
for
$S$
for
![]() $(m_1,m_2)$
to be a well-defined morphism of relations. The domain of
$(m_1,m_2)$
to be a well-defined morphism of relations. The domain of
![]() $G_1\, R$
thus depends on both
$G_1\, R$
thus depends on both
![]() $A$
and
$A$
and
![]() $B$
, rather than simply on
$B$
, rather than simply on
![]() $A$
. Likewise, the codomain of
$A$
. Likewise, the codomain of
![]() $G_1\,R$
also depends on both
$G_1\,R$
also depends on both
![]() $A$
and
$A$
and
![]() $B$
. The domain and codomain therefore cannot simply be
$B$
. The domain and codomain therefore cannot simply be
![]() $G_0\, A$
and
$G_0\, A$
and
![]() $G_0\, B$
, respectively. This suggests that GADTs might fail to have relational interpretations, and thus might fail to have parametric models, as described in the previous paragraph.
$G_0\, B$
, respectively. This suggests that GADTs might fail to have relational interpretations, and thus might fail to have parametric models, as described in the previous paragraph.
We can make this informal argument formal by providing a concrete counterexample. Consider again the GADT
![]() $\mathsf{G}$
given by (10). The set functorial completion interpretation of
$\mathsf{G}$
given by (10). The set functorial completion interpretation of
![]() $\mathsf{G}$
is
$\mathsf{G}$
is
![]() $\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1$
, i.e., is, by the reasoning of Example
4, the identity functor on
$\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1$
, i.e., is, by the reasoning of Example
4, the identity functor on
![]() $\mathit{Set}$
. By the exact same reasoning, this time in
$\mathit{Set}$
. By the exact same reasoning, this time in
![]() $\mathit{Rel}$
rather than in
$\mathit{Rel}$
rather than in
![]() $\mathit{Set}$
, the relational functorial completion interpretation of
$\mathit{Set}$
, the relational functorial completion interpretation of
![]() $\mathsf{G}$
is
$\mathsf{G}$
is
![]() $\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \,\lambda u.\,\mathit{I}_1$
, where
$\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \,\lambda u.\,\mathit{I}_1$
, where
![]() $\lambda u.\,\mathit{I}_1$
is the constantly
$\lambda u.\,\mathit{I}_1$
is the constantly
![]() $\mathit{I}_1$
-valued functor from the category
$\mathit{I}_1$
-valued functor from the category
![]() $\mathit{Rel}\,^0$
with a single object to
$\mathit{Rel}\,^0$
with a single object to
![]() $\mathit{Rel}$
. Indeed, this interpretation is still a left Kan extension, but now it is the left Kan extension determined by the functor interpreting
$\mathit{Rel}$
. Indeed, this interpretation is still a left Kan extension, but now it is the left Kan extension determined by the functor interpreting
![]() $\mathsf{\lambda u. 1}$
in
$\mathsf{\lambda u. 1}$
in
![]() $\mathit{Rel}$
. For the Identity Extension Lemma to hold, for every relation
$\mathit{Rel}$
. For the Identity Extension Lemma to hold, for every relation
![]() $R \in \mathit{Rel}\,(A, B)$
we would need
$R \in \mathit{Rel}\,(A, B)$
we would need
![]() $(\mathit{\mathsf{Lan}}_{\lambda u.\,\mathit{I}_1} \,\lambda u.\,\mathit{I}_1)\, R$
to be a relation between the sets
$(\mathit{\mathsf{Lan}}_{\lambda u.\,\mathit{I}_1} \,\lambda u.\,\mathit{I}_1)\, R$
to be a relation between the sets
![]() $(\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1)\, A$
and
$(\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1)\, A$
and
![]() $(\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1)\,B$
, i.e., between the sets
$(\mathit{Lan}_{\lambda u. 1}\,\lambda u. 1)\,B$
, i.e., between the sets
![]() $A$
and
$A$
and
![]() $B$
. However, this need not be the case.
$B$
. However, this need not be the case.
Consider the relation
![]() $R = (1, 2, 1 \times 2)$
, where
$R = (1, 2, 1 \times 2)$
, where
![]() $1 \times 2$
relates the single element of
$1 \times 2$
relates the single element of
![]() $1$
to both elements of the two-element set
$1$
to both elements of the two-element set
![]() $2$
. We expect
$2$
. We expect
![]() $(\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u.\,\mathit{I}_1)\, R$
to be a relation with domain
$(\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u.\,\mathit{I}_1)\, R$
to be a relation with domain
![]() $1$
. Since left Kan extensions preserve projections (Riehl Reference Riehl2016), we can compute the domain as
$1$
. Since left Kan extensions preserve projections (Riehl Reference Riehl2016), we can compute the domain as
(Note that the left Kan extension of
![]() $\lambda u. \,1$
along
$\lambda u. \,1$
along
![]() $\lambda u.\,\mathit{I}_1$
is a functor from
$\lambda u.\,\mathit{I}_1$
is a functor from
![]() $\mathit{Rel}$
to
$\mathit{Rel}$
to
![]() $\mathit{Set}$
.) By the same reasoning as in Example
4, Proposition 7.1 of (Bush et al. Reference Bush, Leeming and Walters2003) gives that
$\mathit{Set}$
.) By the same reasoning as in Example
4, Proposition 7.1 of (Bush et al. Reference Bush, Leeming and Walters2003) gives that
![]() $(\mathit{Lan}_{\lambda u. \mathit{I}_1} \lambda u. 1)\,R$
can be computed as
$(\mathit{Lan}_{\lambda u. \mathit{I}_1} \lambda u. 1)\,R$
can be computed as
where
![]() $U$
is the unique object of
$U$
is the unique object of
![]() $\mathit{Rel}^0$
,
$\mathit{Rel}^0$
,
![]() $*$
is the unique element of the singleton set
$*$
is the unique element of the singleton set
![]() $1$
, and
$1$
, and
![]() $\approx$
is the smallest equivalence relation such that
$\approx$
is the smallest equivalence relation such that
![]() $(U,m,*)$
and
$(U,m,*)$
and
![]() $(U,m',*)$
are related if
$(U,m',*)$
are related if

commutes, i.e., if
![]() $m = m'$
. Since the relation generating
$m = m'$
. Since the relation generating
![]() $\approx$
is already an equivalence relation, we have that
$\approx$
is already an equivalence relation, we have that
![]() $(U,m,*) \approx (U,m', *)$
iff
$(U,m,*) \approx (U,m', *)$
iff
![]() $m = m'$
. Thus, up to isomorphism,
$m = m'$
. Thus, up to isomorphism,
![]() $(\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u. \,1)\, R = \{ m : \mathit{I}_1 \to R\}$
. But this set is
$(\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u. \,1)\, R = \{ m : \mathit{I}_1 \to R\}$
. But this set is
![]() $\{(!, k_0), (!, k_1)\}$
, where
$\{(!, k_0), (!, k_1)\}$
, where
![]() $k_0, k_1 : 1 \to 2$
are the constantly
$k_0, k_1 : 1 \to 2$
are the constantly
![]() $0$
-valued and
$0$
-valued and
![]() $1$
-valued functions in
$1$
-valued functions in
![]() $\mathit{Set}$
, respectively, and therefore
$\mathit{Set}$
, respectively, and therefore
![]() $\pi _1\,\big ( (\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u.\,\mathit{I}_1) \, R \big )$
is not
$\pi _1\,\big ( (\mathit{Lan}_{\lambda u.\,\mathit{I}_1} \lambda u.\,\mathit{I}_1) \, R \big )$
is not
![]() $1$
, as would be needed for the Identity Extension Lemma to hold. Since the Identity Extension Lemma does not hold for models in which GADTs are interpreted by their functorial completions, such models cannot possibly be parametric.
$1$
, as would be needed for the Identity Extension Lemma to hold. Since the Identity Extension Lemma does not hold for models in which GADTs are interpreted by their functorial completions, such models cannot possibly be parametric.
It is actually possible to construct a simpler counterexample to the Identity Extension Lemma for functorial completion interpretations of GADTs using the relation
![]() $R = (1,\emptyset, \emptyset )$
. However, this relation is somewhat artificial, in the sense that its domain is larger than is strictly necessary to define an empty relation. Since it is also too degenerate to properly expose the mismatch between left Kan extensions at the level of sets and left Kan extensions at the level of relations, we give the above example using the relation
$R = (1,\emptyset, \emptyset )$
. However, this relation is somewhat artificial, in the sense that its domain is larger than is strictly necessary to define an empty relation. Since it is also too degenerate to properly expose the mismatch between left Kan extensions at the level of sets and left Kan extensions at the level of relations, we give the above example using the relation
![]() $(1,2,1 \times 2)$
instead.
$(1,2,1 \times 2)$
instead.
One way to read the result of this subsection is as in (Johann et al. Reference Johann, Ghiorzi and Jeffries2021): if we interpret types in
![]() $\mathit{Set}$
and
$\mathit{Set}$
and
![]() $n$
-ary GADTs as functors from
$n$
-ary GADTs as functors from
![]() $\mathit{Set}^n$
to
$\mathit{Set}^n$
to
![]() $\mathit{Set}$
, then, as with software engineering’s iron triangle, we can have any two of GADTs, functoriality, and parametricity we like, but we cannot have all three.
$\mathit{Set}$
, then, as with software engineering’s iron triangle, we can have any two of GADTs, functoriality, and parametricity we like, but we cannot have all three.
6. Functorial Interpretations in
 $\mathit{PSet}$
and Beyond
$\mathit{PSet}$
and Beyond
We have seen in Section 4.1 that interpreting GADTs as their functorial completions is unsatisfactory. We note, however, that partiality is inherent in the syntax of GADTs. Indeed, one way to understand Examples 1 and 2 is as showing that the map functions for
![]() $\mathsf{Seq}$
, as well as for
$\mathsf{Seq}$
, as well as for
![]() $\mathsf{Eq}$
(and thus those for all proper GADTs), do not map arbitrary functions over their elements. That is, proper GADTs’ map functions are only partially defined (Johann and Cagne Reference Johann, Cagne and Sergey2022; Johann and Ghani Reference Johann and Ghani2008; Johann and Polonsky Reference Johann and Polonsky2019). To interpret GADTs as functors without adding ghost elements to their interpretations, the category in which we interpret them must therefore account for partial functions.
$\mathsf{Eq}$
(and thus those for all proper GADTs), do not map arbitrary functions over their elements. That is, proper GADTs’ map functions are only partially defined (Johann and Cagne Reference Johann, Cagne and Sergey2022; Johann and Ghani Reference Johann and Ghani2008; Johann and Polonsky Reference Johann and Polonsky2019). To interpret GADTs as functors without adding ghost elements to their interpretations, the category in which we interpret them must therefore account for partial functions.
To find a semantics of GADTs that accounts for the partiality of their map functions, we need to allow the functorial actions of GADTs’ interpretations to yield partial functions. However, the interpretations of the functions that are representable in syntax and don’t involve mapping over elements of GADTs should still be total. That is, we seek categories
![]() $\mathscr{C}$
that capture partiality in the computationally relevant sense that once a computation diverges it does not become defined again, and in which
$\mathscr{C}$
that capture partiality in the computationally relevant sense that once a computation diverges it does not become defined again, and in which
![]() $\mathit{Set}$
embeds in such a way that it can be considered the subcategory of “total morphisms” of
$\mathit{Set}$
embeds in such a way that it can be considered the subcategory of “total morphisms” of
![]() $\mathscr{C}$
for some reasonable notion of totality. Obviously, the category
$\mathscr{C}$
for some reasonable notion of totality. Obviously, the category
![]() $\mathit{PSet}$
of sets and partial functions between them is such a category
$\mathit{PSet}$
of sets and partial functions between them is such a category
![]() $\mathscr{C}$
since morphisms there propagate undefinedness. But rather than focusing on the specific category
$\mathscr{C}$
since morphisms there propagate undefinedness. But rather than focusing on the specific category
![]() $\mathit{PSet}$
, we present here an abstract framework that encompasses much more. The advantage of introducing a framework is two-fold. First, our main result (Theorem 18) holds in categories more general than
$\mathit{PSet}$
, we present here an abstract framework that encompasses much more. The advantage of introducing a framework is two-fold. First, our main result (Theorem 18) holds in categories more general than
![]() $\mathit{PSet}$
, including exotic categories
$\mathit{PSet}$
, including exotic categories
![]() $\mathscr{C}$
in which
$\mathscr{C}$
in which
![]() $\mathit{Set}$
embeds nicely as a subcategory of total morphisms. And secondly, the framework does not require that the category of total morphisms is
$\mathit{Set}$
embeds nicely as a subcategory of total morphisms. And secondly, the framework does not require that the category of total morphisms is
![]() $\mathit{Set}$
specifically. The latter entails that Theorem 18 holds not just when the subcategory of total morphisms is
$\mathit{Set}$
specifically. The latter entails that Theorem 18 holds not just when the subcategory of total morphisms is
![]() $\mathit{Set}$
, but when it is any locally presentable category in which ADTs and nested types can be given their standard IAS.
$\mathit{Set}$
, but when it is any locally presentable category in which ADTs and nested types can be given their standard IAS.
The reader may wonder why we develop an abstract framework for our results about interpreting GADTs as functors in
![]() $\mathit{PSet}$
, but were content to restrict attention to the specific category
$\mathit{PSet}$
, but were content to restrict attention to the specific category
![]() $\mathit{Set}$
in the previous sections even though, as noted there, we could also have developed the results in those sections for arbitrary locally presentable categories. The main reason is that how to move from
$\mathit{Set}$
in the previous sections even though, as noted there, we could also have developed the results in those sections for arbitrary locally presentable categories. The main reason is that how to move from
![]() $\mathit{Set}$
to locally presentable categories is well-known in the literature, so moving to the more abstract setting in Sections 2 through 5 provides no additional insights that cannot be gleaned from
$\mathit{Set}$
to locally presentable categories is well-known in the literature, so moving to the more abstract setting in Sections 2 through 5 provides no additional insights that cannot be gleaned from
![]() $\mathit{Set}$
. On the other hand, how to move from
$\mathit{Set}$
. On the other hand, how to move from
![]() $\mathit{PSet}$
to more general categories
$\mathit{PSet}$
to more general categories
![]() $\mathscr{C}$
of the kind we seek now has not previously been known, so the categorical framework for partiality that we provide here is itself part of the contribution of this paper.
$\mathscr{C}$
of the kind we seek now has not previously been known, so the categorical framework for partiality that we provide here is itself part of the contribution of this paper.
We now identify those categories capturing computationally relevant partiality. We then show in Theorem 18 that any semantics in such a category is trivial if we insist that the interpretations of GADTs in them must extend to functors. Given a category
![]() $\mathscr{C}$
, we write
$\mathscr{C}$
, we write
![]() $\operatorname{\mathsf{Mor}}(\mathscr{C})$
for its (possibily large) set of morphisms. We begin by recalling two classic definitions, the first of which “categorifies” the notion of an ideal in monoids.
$\operatorname{\mathsf{Mor}}(\mathscr{C})$
for its (possibily large) set of morphisms. We begin by recalling two classic definitions, the first of which “categorifies” the notion of an ideal in monoids.
Definition 9.
A cosieve in a category
![]() $\mathscr{C}$
is a (possibly large) subset
$\mathscr{C}$
is a (possibly large) subset
![]() $S \subseteq \operatorname{\mathsf{Mor}}(\mathscr{C})$
such that for all morphisms
$S \subseteq \operatorname{\mathsf{Mor}}(\mathscr{C})$
such that for all morphisms
![]() $f: A\to B$
and
$f: A\to B$
and
![]() $g : B\to C$
in
$g : B\to C$
in
![]() $\mathscr{C}$
, if
$\mathscr{C}$
, if
![]() $f\in S$
then
$f\in S$
then
![]() $gf \in S$
.
$gf \in S$
.
Definition 10.
A wide subcategory of a category
![]() $\mathscr{C}$
is a subcategory of
$\mathscr{C}$
is a subcategory of
![]() $\mathscr{C}$
that contains all objects of
$\mathscr{C}$
that contains all objects of
![]() $\mathscr{C}$
.
$\mathscr{C}$
.
If
![]() $\mathscr{D}$
is any subcategory of
$\mathscr{D}$
is any subcategory of
![]() $\mathscr{C}$
, we write
$\mathscr{C}$
, we write
![]() $\overline{\mathscr{D}}$
for the complement of
$\overline{\mathscr{D}}$
for the complement of
![]() $\mathscr{D}$
, i.e., for the (possibly large) set
$\mathscr{D}$
, i.e., for the (possibly large) set
![]() $\operatorname{\mathsf{Mor}}(\mathscr{C}) \setminus \operatorname{\mathsf{Mor}}(\mathscr{D})$
. We can then introduce the following new definition:
$\operatorname{\mathsf{Mor}}(\mathscr{C}) \setminus \operatorname{\mathsf{Mor}}(\mathscr{D})$
. We can then introduce the following new definition:
Definition 11.
A structure of computational partiality on a category
![]() $\mathscr{C}$
is a wide subcategory
$\mathscr{C}$
is a wide subcategory
![]() $\mathscr{D}$
of
$\mathscr{D}$
of
![]() $\mathscr{C}$
such that
$\mathscr{C}$
such that
![]() $\overline{\mathscr{D}}$
is a cosieve.
$\overline{\mathscr{D}}$
is a cosieve.
In a category
![]() $\mathscr{C}$
equipped with a structure of computational partiality
$\mathscr{C}$
equipped with a structure of computational partiality
![]() $\mathscr{D}$
, we call the morphisms of
$\mathscr{D}$
, we call the morphisms of
![]() $\mathscr{D}$
total and those of
$\mathscr{D}$
total and those of
![]() $\overline{\mathscr{D}}$
properly partial. Morphisms of
$\overline{\mathscr{D}}$
properly partial. Morphisms of
![]() $\mathscr{C}$
might be referred to simply as partial. It is not hard to see that
$\mathscr{C}$
might be referred to simply as partial. It is not hard to see that
![]() $\mathit{Set}$
is a structure of computational partiality on
$\mathit{Set}$
is a structure of computational partiality on
![]() $\mathit{PSet}$
and that the terminology introduced in this paragraph accords with what is used there. Indeed, the intuition behind Definition 11 is that
$\mathit{PSet}$
and that the terminology introduced in this paragraph accords with what is used there. Indeed, the intuition behind Definition 11 is that
![]() $\overline{\mathscr D}$
is the collection of computations that are actually undefined on a non-empty set of objects of
$\overline{\mathscr D}$
is the collection of computations that are actually undefined on a non-empty set of objects of
![]() $\mathscr{C}$
(equivalently, of
$\mathscr{C}$
(equivalently, of
![]() $\mathscr{D}$
). Following that intuition, both identities and compositions of total functions must be total functions, and when a function yields an error on an input there is no way to come back from the error by postcomposing with another function. Other categorical frameworks capturing partiality include
$\mathscr{D}$
). Following that intuition, both identities and compositions of total functions must be total functions, and when a function yields an error on an input there is no way to come back from the error by postcomposing with another function. Other categorical frameworks capturing partiality include
![]() $p$
-categories (Robinson and Rosolini Reference Robinson and Rosolini1988), (bi)categories of partial maps (Carboni Reference Carboni1987), categories of partial morphisms (Curien and Obtułowicz Reference Curien and Obtułowicz1989), and restriction categories (Cockett and Lack Reference Cockett and Lack2002). These all give rise to structures of computational partiality.
$p$
-categories (Robinson and Rosolini Reference Robinson and Rosolini1988), (bi)categories of partial maps (Carboni Reference Carboni1987), categories of partial morphisms (Curien and Obtułowicz Reference Curien and Obtułowicz1989), and restriction categories (Cockett and Lack Reference Cockett and Lack2002). These all give rise to structures of computational partiality.
Recall that a split monomorphism
![]() $s : A \to B$
in a category
$s : A \to B$
in a category
![]() $\mathscr{C}$
is a monomorphism in
$\mathscr{C}$
is a monomorphism in
![]() $\mathscr{C}$
for which there exists a morphism
$\mathscr{C}$
for which there exists a morphism
![]() $r : B \to A$
such that
$r : B \to A$
such that
![]() $rs ={id}_A$
. We have the following basic fact about split monomorphisms in a category equipped with a structure of computational partiality:
$rs ={id}_A$
. We have the following basic fact about split monomorphisms in a category equipped with a structure of computational partiality:
Lemma 12. In a category equipped with a structure of computational partiality, split monomorphisms are always total.
Proof.
Let
![]() $s : A \to B$
be a split monomorphism in a category
$s : A \to B$
be a split monomorphism in a category
![]() $\mathscr{C}$
, and suppose
$\mathscr{C}$
, and suppose
![]() $r : B \to A$
is such that
$r : B \to A$
is such that
![]() $rs ={id}_A$
. If
$rs ={id}_A$
. If
![]() $s$
was properly partial in a structure of computational partiality on
$s$
was properly partial in a structure of computational partiality on
![]() $\mathscr{C}$
, then
$\mathscr{C}$
, then
![]() $rs$
, and thus
$rs$
, and thus
![]() ${id}_A$
, would be properly partial as well. But
${id}_A$
, would be properly partial as well. But
![]() ${id}_A$
is total by definition, so it cannot be. Thus,
${id}_A$
is total by definition, so it cannot be. Thus,
![]() $s$
must be total.
$s$
must be total.
Our aim is to consider interpretations of (languages supporting) GADTs in a category
![]() $\mathscr{C}$
equipped with a structure of computational partiality
$\mathscr{C}$
equipped with a structure of computational partiality
![]() $\mathscr{D}$
. However, to do so we require a bit more structure. Specifically,
$\mathscr{D}$
. However, to do so we require a bit more structure. Specifically,
![]() $\mathscr{D}$
must have finite products, and those products in
$\mathscr{D}$
must have finite products, and those products in
![]() $\mathscr{D}$
must extend to
$\mathscr{D}$
must extend to
![]() $\mathscr{C}$
in the sense introduced and justified below.
$\mathscr{C}$
in the sense introduced and justified below.
Definition 13.
Let
![]() $\mathscr{C}$
be a category equipped with a structure of computational partiality
$\mathscr{C}$
be a category equipped with a structure of computational partiality
![]() $\mathscr{D}$
, and write
$\mathscr{D}$
, and write
![]() $\iota : \mathscr{D} \to \mathscr{C}$
for the inclusion functor from
$\iota : \mathscr{D} \to \mathscr{C}$
for the inclusion functor from
![]() $\mathscr{D}$
to
$\mathscr{D}$
to
![]() $\mathscr{C}$
. Suppose further that
$\mathscr{C}$
. Suppose further that
![]() $\mathscr{D}$
has finite products, and write
$\mathscr{D}$
has finite products, and write
![]() $\prod ^{\mathscr{D}}_n : \mathscr{D}^n \to \mathscr{D}$
for the
$\prod ^{\mathscr{D}}_n : \mathscr{D}^n \to \mathscr{D}$
for the
![]() $n$
-ary product functor from
$n$
-ary product functor from
![]() $\mathscr{D}^n$
to
$\mathscr{D}^n$
to
![]() $\mathscr{D}$
. Then the products of
$\mathscr{D}$
. Then the products of
![]() $\mathscr{D}$
extend to
$\mathscr{D}$
extend to
![]() $\mathscr{C}$
if, for each
$\mathscr{C}$
if, for each
![]() $n\geq 0$
, there exists a functor
$n\geq 0$
, there exists a functor
![]() $\bigotimes ^{\mathscr{C}}_n : \mathscr{C}^n \to \mathscr{C}$
such that the following square commutes:
$\bigotimes ^{\mathscr{C}}_n : \mathscr{C}^n \to \mathscr{C}$
such that the following square commutes:

We write
![]() $\times ^{\mathscr{D}}$
and
$\times ^{\mathscr{D}}$
and
![]() $\otimes ^{\mathscr{C}}$
infix rather than
$\otimes ^{\mathscr{C}}$
infix rather than
![]() $\Pi ^{\mathscr{D}}_2$
and
$\Pi ^{\mathscr{D}}_2$
and
![]() $\bigotimes ^{\mathscr{C}}_2$
prefix when
$\bigotimes ^{\mathscr{C}}_2$
prefix when
![]() $n = 2$
. Crucially, even when
$n = 2$
. Crucially, even when
![]() $\mathscr{C}$
has products, the object
$\mathscr{C}$
has products, the object
![]() $\bigotimes ^{\mathscr{C}}_n A_i$
need not be a product of
$\bigotimes ^{\mathscr{C}}_n A_i$
need not be a product of
![]() $A_1$
,…,
$A_1$
,…,
![]() $A_n$
in
$A_n$
in
![]() $\mathscr{C}$
. The following examples help clarify this observation.
$\mathscr{C}$
. The following examples help clarify this observation.
Example 14.
For any category
![]() $\mathscr{C}$
,
$\mathscr{C}$
,
![]() $\mathscr{C}$
itself is (trivially) a structure of computational partiality on
$\mathscr{C}$
itself is (trivially) a structure of computational partiality on
![]() $\mathscr{C}$
. Moreover, if
$\mathscr{C}$
. Moreover, if
![]() $\mathscr{C}$
has finite products, then they extend (trivially) to
$\mathscr{C}$
has finite products, then they extend (trivially) to
![]() $\mathscr{C}$
. For each
$\mathscr{C}$
. For each
![]() $n$
,
$n$
,
![]() $\bigotimes ^{\mathscr{C}}_n$
is simply the actual
$\bigotimes ^{\mathscr{C}}_n$
is simply the actual
![]() $n$
-ary product functor
$n$
-ary product functor
![]() $\prod ^{\mathscr{C}}_n$
.
$\prod ^{\mathscr{C}}_n$
.
Example 15.
The category
![]() $\mathit{Set}$
is a structure of computational partiality on the category
$\mathit{Set}$
is a structure of computational partiality on the category
![]() $\mathit{PSet}$
whose products extend to
$\mathit{PSet}$
whose products extend to
![]() $\mathit{PSet}$
. We consider the case for
$\mathit{PSet}$
. We consider the case for
![]() $n=2$
explicitly; those for other values of
$n=2$
explicitly; those for other values of
![]() $n$
are analogous.
$n$
are analogous.
Define the functor
![]() $\_\otimes \_ : \mathit{PSet}^2 \to \mathit{PSet}$
whose action on objects is given by
$\_\otimes \_ : \mathit{PSet}^2 \to \mathit{PSet}$
whose action on objects is given by
![]() $A_1 \otimes A_2 = A_1 \times A_2$
, where
$A_1 \otimes A_2 = A_1 \times A_2$
, where
![]() $\_\times \_$
denotes the usual cartesian product in
$\_\times \_$
denotes the usual cartesian product in
![]() $\mathit{Set}$
, and whose action on morphisms sends partial functions
$\mathit{Set}$
, and whose action on morphisms sends partial functions
![]() $f_1: A_1 \to B_1$
and
$f_1: A_1 \to B_1$
and
![]() $f_2 : A_2 \to B_2$
to the partial function
$f_2 : A_2 \to B_2$
to the partial function
![]() $f_1 \otimes f_2 : A_1 \times A_2 \to B_1 \times B_2$
given by
$f_1 \otimes f_2 : A_1 \times A_2 \to B_1 \times B_2$
given by
 \begin{align*} (f_1 \otimes f_2) (a_1,a_2) = \left \{ \begin{array}{l@{\quad}l} (f_1(a_1), f_2(a_2)) &\text{ if both $f_1(a_1)$ and $f_2(a_2)$ are defined} \\ \text{undefined} &\text{otherwise} \end{array} \right . \end{align*}
\begin{align*} (f_1 \otimes f_2) (a_1,a_2) = \left \{ \begin{array}{l@{\quad}l} (f_1(a_1), f_2(a_2)) &\text{ if both $f_1(a_1)$ and $f_2(a_2)$ are defined} \\ \text{undefined} &\text{otherwise} \end{array} \right . \end{align*}
Then if
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are total functions,
$f_2$
are total functions,
![]() $f_1\otimes f_2$
is total as well and actually coincides with the cartesian product of
$f_1\otimes f_2$
is total as well and actually coincides with the cartesian product of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in
$f_2$
in
![]() $\mathit{Set}$
. That is, for the inclusion
$\mathit{Set}$
. That is, for the inclusion
![]() $\iota : \mathit{Set} \to \mathit{PSet}$
, we have
$\iota : \mathit{Set} \to \mathit{PSet}$
, we have
![]() $\iota (\_)\otimes \iota (\_) = \iota (\_ \times \_)$
.
$\iota (\_)\otimes \iota (\_) = \iota (\_ \times \_)$
.
Notice, however, that
![]() $f_1 \otimes f_2$
is not the product of
$f_1 \otimes f_2$
is not the product of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
in
$f_2$
in
![]() $\mathit{PSet}$
. Indeed, the product of two objects
$\mathit{PSet}$
. Indeed, the product of two objects
![]() $A_1$
and
$A_1$
and
![]() $A_2$
in
$A_2$
in
![]() $\mathit{PSet}$
is the disjoint union
$\mathit{PSet}$
is the disjoint union
![]() $A_1 + (A_1\times A_2) + A_2$
. Writing
$A_1 + (A_1\times A_2) + A_2$
. Writing
![]() $i$
,
$i$
,
![]() $j$
, and
$j$
, and
![]() $k$
for the three canonical injections into this disjoint union, the product
$k$
for the three canonical injections into this disjoint union, the product
![]() $f_1 \times f_2$
in
$f_1 \times f_2$
in
![]() $\mathit{PSet}$
is the partial function from
$\mathit{PSet}$
is the partial function from
![]() $A_1 + (A_1\times A_2) + A_2$
to
$A_1 + (A_1\times A_2) + A_2$
to
![]() $B_1 + (B_1\times B_2) + B_2$
defined by
$B_1 + (B_1\times B_2) + B_2$
defined by
 \begin{align*} \begin{aligned} (f_1 \times f_2) (i(a_1))\quad \;\;\; &= \;i(f_1(a_1)) \quad &\text{if $f_1(a_1)$ defined} \\ (f_1 \times f_2) (j(a_1,a_2)) &=\; j(f_1(a_1),f_2(a_2))) \quad &\text{if $f_1(a_1)$ and $f_2(a_2)$ both defined} \\ (f_1 \times f_2) (j(a_1,a_2)) &= \;i(f_1(a_1)) \quad &\text{if $f_1(a_1)$ defined and $f_2(a_2)$ undefined} \\ (f_1 \times f_2) (j(a_1,a_2)) &= \;k(f_2(a_2)) \quad &\text{if $f_1(a_1)$ undefined and $f_2(a_2)$ defined} \\ (f_1 \times f_2) (k(a_2))\quad \;\; &= \;k(f_2(a_2)) \quad &\text{if $f_2(a_2)$ defined} \\ (f_1 \times f_2) (x)\quad \quad \quad &= \;\text{undefined} \quad &\text{otherwise} \\ \end{aligned} \end{align*}
\begin{align*} \begin{aligned} (f_1 \times f_2) (i(a_1))\quad \;\;\; &= \;i(f_1(a_1)) \quad &\text{if $f_1(a_1)$ defined} \\ (f_1 \times f_2) (j(a_1,a_2)) &=\; j(f_1(a_1),f_2(a_2))) \quad &\text{if $f_1(a_1)$ and $f_2(a_2)$ both defined} \\ (f_1 \times f_2) (j(a_1,a_2)) &= \;i(f_1(a_1)) \quad &\text{if $f_1(a_1)$ defined and $f_2(a_2)$ undefined} \\ (f_1 \times f_2) (j(a_1,a_2)) &= \;k(f_2(a_2)) \quad &\text{if $f_1(a_1)$ undefined and $f_2(a_2)$ defined} \\ (f_1 \times f_2) (k(a_2))\quad \;\; &= \;k(f_2(a_2)) \quad &\text{if $f_2(a_2)$ defined} \\ (f_1 \times f_2) (x)\quad \quad \quad &= \;\text{undefined} \quad &\text{otherwise} \\ \end{aligned} \end{align*}
The square

thus need not commute in
![]() $\mathit{PSet}$
.
$\mathit{PSet}$
.
Example 16.
Consider the category
![]() $\omega \textrm{pCPO}$
of complete partial orders with bottom elements and strict Scott-continuous functions between them. Write
$\omega \textrm{pCPO}$
of complete partial orders with bottom elements and strict Scott-continuous functions between them. Write
![]() $\omega \textrm{pCPO}_{t}$
for the wide subcategory containing only those morphisms
$\omega \textrm{pCPO}_{t}$
for the wide subcategory containing only those morphisms
![]() $f : D \to D'$
such that
$f : D \to D'$
such that
![]() $f^{-1}(\bot _{D'}) = \{\bot _D\}$
, where
$f^{-1}(\bot _{D'}) = \{\bot _D\}$
, where
![]() $\bot _D$
is the bottom element of
$\bot _D$
is the bottom element of
![]() $D$
and
$D$
and
![]() $\bot _{D'}$
is the bottom element of
$\bot _{D'}$
is the bottom element of
![]() $D'$
. The product
$D'$
. The product
![]() $\prod ^{{\omega \textrm{pCPO}_{t}}}_nD_i$
of objects
$\prod ^{{\omega \textrm{pCPO}_{t}}}_nD_i$
of objects
![]() $D_1,\dots,D_n$
in
$D_1,\dots,D_n$
in
![]() $\omega \textrm{pCPO}_{t}$
is the subset of the cartesian product in
$\omega \textrm{pCPO}_{t}$
is the subset of the cartesian product in
![]() $\mathit{Set}$
of the sets underlying the
$\mathit{Set}$
of the sets underlying the
![]() $D_i$
s comprising those tuples
$D_i$
s comprising those tuples
![]() $(x_1,\dots,x_n)$
such that either
$(x_1,\dots,x_n)$
such that either
![]() $x_i = \bot _{D_i}$
for all
$x_i = \bot _{D_i}$
for all
![]() $i$
or
$i$
or
![]() $x_i \neq \bot _{D_i}$
for all
$x_i \neq \bot _{D_i}$
for all
![]() $i$
. The product
$i$
. The product
![]() $\prod ^{{\omega \textrm{pCPO}_{t}}}_nf_i$
of morphims
$\prod ^{{\omega \textrm{pCPO}_{t}}}_nf_i$
of morphims
![]() $f_1:D_1\to D_1^{\prime},\dots,f_n:D_n\to D_n^{\prime}$
in
$f_1:D_1\to D_1^{\prime},\dots,f_n:D_n\to D_n^{\prime}$
in
![]() $\omega \textrm{pCPO}_{t}$
maps
$\omega \textrm{pCPO}_{t}$
maps
![]() $(x_1,\dots,x_n)$
to
$(x_1,\dots,x_n)$
to
![]() $(\bot _{D_1^{\prime}},\dots,\bot _{D_n^{\prime}})$
if
$(\bot _{D_1^{\prime}},\dots,\bot _{D_n^{\prime}})$
if
![]() $x_i = \bot _{D_i}$
for some
$x_i = \bot _{D_i}$
for some
![]() $i$
, and maps
$i$
, and maps
![]() $(x_1,\dots,x_n)$
to
$(x_1,\dots,x_n)$
to
![]() $(f_1(x_1),\dots,f_n(x_n))$
otherwise. The category
$(f_1(x_1),\dots,f_n(x_n))$
otherwise. The category
![]() $\omega \textrm{pCPO}_{t}$
is thus a structure of computational partiality on
$\omega \textrm{pCPO}_{t}$
is thus a structure of computational partiality on
![]() $\omega \textrm{pCPO}$
whose products extend to
$\omega \textrm{pCPO}$
whose products extend to
![]() $\omega \textrm{pCPO}$
. Indeed, if
$\omega \textrm{pCPO}$
. Indeed, if
![]() $f_i : D_i \to D'_i$
,
$f_i : D_i \to D'_i$
,
![]() $i = 1,\ldots,n$
, are strict Scott-continuous functions, then there is a strict Scott-continuous function
$i = 1,\ldots,n$
, are strict Scott-continuous functions, then there is a strict Scott-continuous function
![]() $\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i: \prod ^{{\omega \textrm{pCPO}_{t}}}_nD_i \to \prod ^{{\omega \textrm{pCPO}_{t}}}_nD'_i$
that maps
$\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i: \prod ^{{\omega \textrm{pCPO}_{t}}}_nD_i \to \prod ^{{\omega \textrm{pCPO}_{t}}}_nD'_i$
that maps
![]() $(x_1,\dots,x_n)$
to
$(x_1,\dots,x_n)$
to
![]() $(\bot _{D_1^{\prime}},\dots,\bot _{D_n^{\prime}})$
if
$(\bot _{D_1^{\prime}},\dots,\bot _{D_n^{\prime}})$
if
![]() $f_i (x_i) = \bot _{D_i^{\prime}}$
for some
$f_i (x_i) = \bot _{D_i^{\prime}}$
for some
![]() $i$
, and maps
$i$
, and maps
![]() $(x_1,\dots,x_n)$
to
$(x_1,\dots,x_n)$
to
![]() $(f_1(x_1),\dots,f_n(x_n))$
otherwise. Note that if each
$(f_1(x_1),\dots,f_n(x_n))$
otherwise. Note that if each
![]() $f_i$
is in
$f_i$
is in
![]() $\omega \textrm{pCPO}_{t}$
then
$\omega \textrm{pCPO}_{t}$
then
![]() $\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i$
is as well and actually coincides with the product of the
$\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i$
is as well and actually coincides with the product of the
![]() $f_i$
s in
$f_i$
s in
![]() $\omega \textrm{pCPO}_{t}$
. Moreover, the construction above is clearly functorial in the
$\omega \textrm{pCPO}_{t}$
. Moreover, the construction above is clearly functorial in the
![]() $f_i$
s. Thus, for the inclusion
$f_i$
s. Thus, for the inclusion
![]() $\iota :{\omega \textrm{pCPO}_{t}} \to{\omega \textrm{pCPO}}$
, we have
$\iota :{\omega \textrm{pCPO}_{t}} \to{\omega \textrm{pCPO}}$
, we have
![]() ${\bigotimes _n^{{\omega \textrm{pCPO}}}} \circ \iota ^n = \iota \circ \prod _n^{{\omega \textrm{pCPO}_{t}}}$
.
${\bigotimes _n^{{\omega \textrm{pCPO}}}} \circ \iota ^n = \iota \circ \prod _n^{{\omega \textrm{pCPO}_{t}}}$
.
Note, however, that
![]() $\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i$
is not the product of
$\bigotimes ^{{\omega \textrm{pCPO}}}_n f_i$
is not the product of
![]() $f_1,\dots,f_n$
in
$f_1,\dots,f_n$
in
![]() $\omega \textrm{pCPO}$
. The product
$\omega \textrm{pCPO}$
. The product
![]() $\Pi ^{{\omega \textrm{pCPO}}}_n D_i$
of
$\Pi ^{{\omega \textrm{pCPO}}}_n D_i$
of
![]() $D_1,\dots,D_n$
in
$D_1,\dots,D_n$
in
![]() $\omega \textrm{pCPO}$
is the cartesian product of the sets underlying the
$\omega \textrm{pCPO}$
is the cartesian product of the sets underlying the
![]() $D_i$
s, ordered componentwise, and the product
$D_i$
s, ordered componentwise, and the product
![]() $\Pi ^{{\omega \textrm{pCPO}}}_n f_i : \prod ^{{\omega \textrm{pCPO}}}_n D_i \to \prod ^{{\omega \textrm{pCPO}}}_n D'_i$
in
$\Pi ^{{\omega \textrm{pCPO}}}_n f_i : \prod ^{{\omega \textrm{pCPO}}}_n D_i \to \prod ^{{\omega \textrm{pCPO}}}_n D'_i$
in
![]() $\omega \textrm{pCPO}$
of morphisms
$\omega \textrm{pCPO}$
of morphisms
![]() $f_i : D_i \to D_i^{\prime}$
is the morphism mapping
$f_i : D_i \to D_i^{\prime}$
is the morphism mapping
![]() $(x_1,\dots,x_n)$
to
$(x_1,\dots,x_n)$
to
![]() $(f_1(x_1),\dots,f_n(x_n))$
. Writing
$(f_1(x_1),\dots,f_n(x_n))$
. Writing
![]() $j_{X_1,\dots,X_n}$
for the canonical inclusion of
$j_{X_1,\dots,X_n}$
for the canonical inclusion of
![]() $\prod ^{{\omega \textrm{pCPO}_{t}}}_n X_i$
into
$\prod ^{{\omega \textrm{pCPO}_{t}}}_n X_i$
into
![]() $\prod ^{{\omega \textrm{pCPO}}}_n X_i$
, we thus see that the square
$\prod ^{{\omega \textrm{pCPO}}}_n X_i$
, we thus see that the square

need not commute in
![]() $\omega \textrm{pCPO}$
.
$\omega \textrm{pCPO}$
.
Now fix a category
![]() $\mathscr{C}$
equipped with a structure of computational partiality
$\mathscr{C}$
equipped with a structure of computational partiality
![]() $\mathscr{D}$
. Suppose that
$\mathscr{D}$
. Suppose that
![]() $\mathscr{D}$
has finite products and that they extend to
$\mathscr{D}$
has finite products and that they extend to
![]() $\mathscr{C}$
. We want to define a good notion of an interpretation of (a language supporting) GADTs in
$\mathscr{C}$
. We want to define a good notion of an interpretation of (a language supporting) GADTs in
![]() $(\mathscr{C},\mathscr{D})$
. Although we want to remain as language-agnostic as possible, so that our result can be replayed in as many different settings as possible, we must still make some reasonable assumptions about the type theory underlying the ambient language. Such a type theory necessarily describes how to construct types from a given context of type variables, and how to construct typed terms from a given context of typed term variables. It should also come with a mechanism (such as an operational semantics) that verifies that a term is terminating. Non-terminating terms represent those programs that loop infinitely or are undefined on certain inputs. Terminating terms represent those programs that compute actual values in finite time.
$(\mathscr{C},\mathscr{D})$
. Although we want to remain as language-agnostic as possible, so that our result can be replayed in as many different settings as possible, we must still make some reasonable assumptions about the type theory underlying the ambient language. Such a type theory necessarily describes how to construct types from a given context of type variables, and how to construct typed terms from a given context of typed term variables. It should also come with a mechanism (such as an operational semantics) that verifies that a term is terminating. Non-terminating terms represent those programs that loop infinitely or are undefined on certain inputs. Terminating terms represent those programs that compute actual values in finite time.
The key idea guiding Definition 17 below is to interpret contexts (and thus types) by objects of
![]() $\mathscr{C}$
and to interpret terms by morphisms of
$\mathscr{C}$
and to interpret terms by morphisms of
![]() $\mathscr{C}$
in such a way that the interpretations of terminating terms are actually in
$\mathscr{C}$
in such a way that the interpretations of terminating terms are actually in
![]() $\mathscr{D}$
. With this in mind, we are led to interpret a context
$\mathscr{D}$
. With this in mind, we are led to interpret a context
![]() $\Gamma$
comprising variables of types
$\Gamma$
comprising variables of types
![]() $\mathsf{a}_1,\dots,\mathsf{a}_n$
as the product
$\mathsf{a}_1,\dots,\mathsf{a}_n$
as the product
![]() $\Pi ^{\mathscr{D}}_n[\![\mathsf{a}_i]\!]$
in
$\Pi ^{\mathscr{D}}_n[\![\mathsf{a}_i]\!]$
in
![]() $\mathscr{D}$
of the interpretations
$\mathscr{D}$
of the interpretations
![]() $[\![\mathsf{a}_i]\!]$
of
$[\![\mathsf{a}_i]\!]$
of
![]() $\mathsf{a}_i$
for
$\mathsf{a}_i$
for
![]() $i = 1,\ldots,n$
. Now, in any context
$i = 1,\ldots,n$
. Now, in any context
![]() $\Gamma$
, we can always define the term that picks out the
$\Gamma$
, we can always define the term that picks out the
![]() $i^{th}$
variable: it is a terminating term (it represents the program that takes
$i^{th}$
variable: it is a terminating term (it represents the program that takes
![]() $n$
inputs and simply returns the
$n$
inputs and simply returns the
![]() $i^{th}$
), so its interpretation must be a morphism
$i^{th}$
), so its interpretation must be a morphism
![]() $\pi _i : [\![\Gamma ]\!] \to [\![\mathsf{a}_i]\!]$
in
$\pi _i : [\![\Gamma ]\!] \to [\![\mathsf{a}_i]\!]$
in
![]() $\mathscr{D}$
. To see that
$\mathscr{D}$
. To see that
![]() $[\![\Gamma ]\!]$
, together with the
$[\![\Gamma ]\!]$
, together with the
![]() $\pi _i$
s, actually constitute a product in
$\pi _i$
s, actually constitute a product in
![]() $\mathscr{D}$
, we have to turn to the rules that govern the production of morphisms of contexts in the underlying type theory. A morphism from a context
$\mathscr{D}$
, we have to turn to the rules that govern the production of morphisms of contexts in the underlying type theory. A morphism from a context
![]() $\Delta$
to a context
$\Delta$
to a context
![]() $\Gamma$
is given by a term of type
$\Gamma$
is given by a term of type
![]() $\mathsf{a}$
in context
$\mathsf{a}$
in context
![]() $\Delta$
for each type
$\Delta$
for each type
![]() $\mathsf{a}$
appearing in
$\mathsf{a}$
appearing in
![]() $\Gamma$
. Such a morphism of contexts is considered terminating only if each of the terms defining it is terminating; this corresponds to the intuitive expectation that the simultaneous run of the programs represented by the terms terminates successfully if and only if each of the runs terminates individually. This programming language feature can be expressed in the semantics by requiring that
$\Gamma$
. Such a morphism of contexts is considered terminating only if each of the terms defining it is terminating; this corresponds to the intuitive expectation that the simultaneous run of the programs represented by the terms terminates successfully if and only if each of the runs terminates individually. This programming language feature can be expressed in the semantics by requiring that
![]() $[\![\Gamma ]\!]$
has the following property: for any object
$[\![\Gamma ]\!]$
has the following property: for any object
![]() $C$
of
$C$
of
![]() $\mathscr{C}$
, every tuple of morphisms
$\mathscr{C}$
, every tuple of morphisms
![]() $f_i : C \to [\![\mathsf{a}_i]\!]$
in
$f_i : C \to [\![\mathsf{a}_i]\!]$
in
![]() $\mathscr{C}$
defines a morphism
$\mathscr{C}$
defines a morphism
![]() $f: C\to [\![\Gamma ]\!]$
in
$f: C\to [\![\Gamma ]\!]$
in
![]() $\mathscr{C}$
. Moreover,
$\mathscr{C}$
. Moreover,
![]() $f$
is in
$f$
is in
![]() $\mathscr{D}$
whenever all the
$\mathscr{D}$
whenever all the
![]() $f_i$
s are, in which case
$f_i$
s are, in which case
![]() $f_i = \pi _i f$
for
$f_i = \pi _i f$
for
![]() $i = 1,\dots,n$
, and
$i = 1,\dots,n$
, and
![]() $f$
is uniquely determined by the
$f$
is uniquely determined by the
![]() $f_i$
s. In other words,
$f_i$
s. In other words,
![]() $[\![\Gamma ]\!]$
, together with the
$[\![\Gamma ]\!]$
, together with the
![]() $\pi _i$
s, is a product of the
$\pi _i$
s, is a product of the
![]() $[\![\mathsf{a}_i]\!]$
s in
$[\![\mathsf{a}_i]\!]$
s in
![]() $\mathscr{D}$
.
$\mathscr{D}$
.
Now that we have established that it is natural to interpret each context
![]() $\Gamma$
as the product
$\Gamma$
as the product
![]() $\prod ^{\mathscr{D}}_n[\![\mathsf{a}_i]\!]$
in
$\prod ^{\mathscr{D}}_n[\![\mathsf{a}_i]\!]$
in
![]() $\mathscr{D}$
of the types
$\mathscr{D}$
of the types
![]() $\mathsf{a}_i$
,
$\mathsf{a}_i$
,
![]() $i = 1,\dots,n$
, it comprises, we explain why it is equally natural to expect the products of
$i = 1,\dots,n$
, it comprises, we explain why it is equally natural to expect the products of
![]() $\mathscr{D}$
to extend to
$\mathscr{D}$
to extend to
![]() $\mathscr{C}$
. We focus on the case
$\mathscr{C}$
. We focus on the case
![]() $n=2$
for illustrational purposes. Suppose we are given terms
$n=2$
for illustrational purposes. Suppose we are given terms
![]() $\mathsf{t}_1$
of type
$\mathsf{t}_1$
of type
![]() $\mathsf{b}_1$
and
$\mathsf{b}_1$
and
![]() $\mathsf{t}_2$
of type
$\mathsf{t}_2$
of type
![]() $\mathsf{b}_2$
in context
$\mathsf{b}_2$
in context
![]() $\Gamma$
, and suppose
$\Gamma$
, and suppose
![]() $\mathsf{t}_1$
and
$\mathsf{t}_1$
and
![]() $\mathsf{t}_2$
are interpreted by morphisms
$\mathsf{t}_2$
are interpreted by morphisms
![]() $[\![\mathsf{t}_1]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_1]\!]$
and
$[\![\mathsf{t}_1]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_1]\!]$
and
![]() $[\![\mathsf{t}_2]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_2]\!]$
in
$[\![\mathsf{t}_2]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_2]\!]$
in
![]() $\mathscr{C}$
, respectively. Write
$\mathscr{C}$
, respectively. Write
![]() $\Gamma '$
for the context containing only a variable of type
$\Gamma '$
for the context containing only a variable of type
![]() $\mathsf{b}_1$
and a variable of type
$\mathsf{b}_1$
and a variable of type
![]() $\mathsf{b}_2$
. We need to be able to construct the interpretation of the morphism of contexts from
$\mathsf{b}_2$
. We need to be able to construct the interpretation of the morphism of contexts from
![]() $\Gamma$
to
$\Gamma$
to
![]() $\Gamma '$
given by the pair
$\Gamma '$
given by the pair
![]() $(\mathsf{t}_1, \mathsf{t}_2)$
. That is, we want to construct from
$(\mathsf{t}_1, \mathsf{t}_2)$
. That is, we want to construct from
![]() $[\![\mathsf{t}_1]\!]$
and
$[\![\mathsf{t}_1]\!]$
and
![]() $[\![\mathsf{t}_2]\!]$
a morphism
$[\![\mathsf{t}_2]\!]$
a morphism
![]() $[\![(\mathsf{t}_1, \mathsf{t}_2)]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_1]\!]\times ^{\mathscr{D}} [\![\mathsf{b}_2]\!]$
in
$[\![(\mathsf{t}_1, \mathsf{t}_2)]\!] : [\![\Gamma ]\!] \to [\![\mathsf{b}_1]\!]\times ^{\mathscr{D}} [\![\mathsf{b}_2]\!]$
in
![]() $\mathscr{C}$
. Moreover, when
$\mathscr{C}$
. Moreover, when
![]() $\mathsf{t}_1$
and
$\mathsf{t}_1$
and
![]() $\mathsf{t}_2$
are terminating terms, their interpretations are morphisms of
$\mathsf{t}_2$
are terminating terms, their interpretations are morphisms of
![]() $\mathscr{D}$
and we want
$\mathscr{D}$
and we want
![]() $[\![(\mathsf{t}_1, \mathsf{t}_2)]\!]$
to be in
$[\![(\mathsf{t}_1, \mathsf{t}_2)]\!]$
to be in
![]() $\mathscr{D}$
as well. In addition, in that case we want to recover the usual interpretation of morphisms of contexts, i.e., we want
$\mathscr{D}$
as well. In addition, in that case we want to recover the usual interpretation of morphisms of contexts, i.e., we want
![]() $[\![(\mathsf{t}_1,\mathsf{t}_2)]\!]$
to be the morphism
$[\![(\mathsf{t}_1,\mathsf{t}_2)]\!]$
to be the morphism
in
![]() $\mathscr{D}$
. (Note that
$\mathscr{D}$
. (Note that
![]() $\textrm{diag}$
is a morphism in
$\textrm{diag}$
is a morphism in
![]() $\mathscr{D}$
.) When
$\mathscr{D}$
.) When
![]() $[\![\mathsf{t}_1]\!]$
and
$[\![\mathsf{t}_1]\!]$
and
![]() $[\![\mathsf{t}_2]\!]$
are not total, this construction cannot be done unless the product
$[\![\mathsf{t}_2]\!]$
are not total, this construction cannot be done unless the product
![]() $\_\times ^{\mathscr{D}}\_$
of
$\_\times ^{\mathscr{D}}\_$
of
![]() $\mathscr{D}$
extends to
$\mathscr{D}$
extends to
![]() $\mathscr{C}$
as a functor
$\mathscr{C}$
as a functor
![]() $\_\otimes \_$
. In this case, we can define
$\_\otimes \_$
. In this case, we can define
![]() $[\![(\mathsf{t}_1,\mathsf{t}_2)]\!]$
to be the morphism
$[\![(\mathsf{t}_1,\mathsf{t}_2)]\!]$
to be the morphism
in
![]() $\mathscr{C}$
.
$\mathscr{C}$
.
Definition 17.
Let
![]() $\mathscr{C}$
be a category equipped with a structure of computational partiality
$\mathscr{C}$
be a category equipped with a structure of computational partiality
![]() $\mathscr{D}$
. Suppose further that
$\mathscr{D}$
. Suppose further that
![]() $\mathscr{D}$
has finite products, and that these extend to
$\mathscr{D}$
has finite products, and that these extend to
![]() $\mathscr{C}$
. An interpretation
$\mathscr{C}$
. An interpretation
![]() $[\![\_]\!]$
of (a language supporting) GADTs in
$[\![\_]\!]$
of (a language supporting) GADTs in
![]() $(\mathscr{C},\mathscr{D})$
associates to each closed type
$(\mathscr{C},\mathscr{D})$
associates to each closed type
![]() $\mathsf{a}$
an object
$\mathsf{a}$
an object
![]() $[\![\mathsf{a}]\!]$
of
$[\![\mathsf{a}]\!]$
of
![]() $\mathscr{C}$
, and to each term
$\mathscr{C}$
, and to each term
![]() $\mathsf{t}$
of type
$\mathsf{t}$
of type
![]() $\mathsf{a}$
in context
$\mathsf{a}$
in context
![]() $\Gamma$
comprising variables of types
$\Gamma$
comprising variables of types
![]() $\mathsf{a}_1,\dots,\mathsf{a}_n$
, a morphism
$\mathsf{a}_1,\dots,\mathsf{a}_n$
, a morphism
![]() $[\![\mathsf{t}]\!] : \prod ^{\mathscr{D}}_n [\![\mathsf{a}_i]\!] \to [\![\mathsf{a}]\!]$
in
$[\![\mathsf{t}]\!] : \prod ^{\mathscr{D}}_n [\![\mathsf{a}_i]\!] \to [\![\mathsf{a}]\!]$
in
![]() $\mathscr{C}$
such that
$\mathscr{C}$
such that
![]() $[\![\mathsf{t}]\!]$
is in
$[\![\mathsf{t}]\!]$
is in
![]() $\mathscr{D}$
when
$\mathscr{D}$
when
![]() $\mathsf{t}$
is terminating. We require that
$\mathsf{t}$
is terminating. We require that
![]() $[\![\_]\!]$
maps the unit type
$[\![\_]\!]$
maps the unit type
![]() $\top$
to
$\top$
to
![]() $1$
and term-substitution to composition in
$1$
and term-substitution to composition in
![]() $\mathscr{C}$
. Given a
$\mathscr{C}$
. Given a
![]() $n$
-ary GADT
$n$
-ary GADT
![]() $\mathsf{G}$
, a functor
$\mathsf{G}$
, a functor
![]() $[\![\mathsf{G}]\!] :\mathscr{C}^n \to \mathscr{C}$
is said to manifest
$[\![\mathsf{G}]\!] :\mathscr{C}^n \to \mathscr{C}$
is said to manifest
![]() $\mathsf{G}$
relative to
$\mathsf{G}$
relative to
![]() $[\![\_]\!]$
if the action of
$[\![\_]\!]$
if the action of
![]() $[\![\mathsf{G}]\!]$
on every object of the form
$[\![\mathsf{G}]\!]$
on every object of the form
![]() $([\![\mathsf{a}_1]\!],\dots,[\![\mathsf{a}_n]\!])$
is precisely
$([\![\mathsf{a}_1]\!],\dots,[\![\mathsf{a}_n]\!])$
is precisely
![]() $[\![\mathsf{G}\, \mathsf{a}_1 \dots \mathsf{a}_n]\!]$
.
$[\![\mathsf{G}\, \mathsf{a}_1 \dots \mathsf{a}_n]\!]$
.
When
![]() $\mathscr{C}$
is
$\mathscr{C}$
is
![]() $\mathit{Set}$
(or any other locally presentable category), Definition 17 recovers the functorial semantics for GADTs in
$\mathit{Set}$
(or any other locally presentable category), Definition 17 recovers the functorial semantics for GADTs in
![]() $\mathit{Set}$
(or, more generally, in
$\mathit{Set}$
(or, more generally, in
![]() $\mathscr{C}$
) used in Sections 2 through 5 by taking
$\mathscr{C}$
) used in Sections 2 through 5 by taking
![]() $\mathscr{D}$
to be
$\mathscr{D}$
to be
![]() $\mathscr{C}$
as in Example 14. This perfectly captures the fact that all morphisms are total in that semantics.
$\mathscr{C}$
as in Example 14. This perfectly captures the fact that all morphisms are total in that semantics.
We can now prove that, like functorial interpretations of GADTs in
![]() $\mathit{Set}$
, functorial interpretations of GADTs in more general categories equipped with structures of computational partiality are also insufficient.
$\mathit{Set}$
, functorial interpretations of GADTs in more general categories equipped with structures of computational partiality are also insufficient.
Theorem 18.
Let
![]() $\mathscr{C}$
be a category equipped with structure of computational partiality
$\mathscr{C}$
be a category equipped with structure of computational partiality
![]() $\mathscr{D}$
. Suppose
$\mathscr{D}$
. Suppose
![]() $[\![\_]\!]$
is an interpretation of GADTs in
$[\![\_]\!]$
is an interpretation of GADTs in
![]() $(\mathscr{C}, \mathscr{D})$
relative to which each GADT is manifested by a functor. Then
$(\mathscr{C}, \mathscr{D})$
relative to which each GADT is manifested by a functor. Then
![]() $[\![\mathsf{a}]\!] \simeq 1$
for all closed types
$[\![\mathsf{a}]\!] \simeq 1$
for all closed types
![]() $\mathsf{a}$
containing terminating terms.
$\mathsf{a}$
containing terminating terms.
Proof.
Among the GADTs in our language is the GADT
![]() $\mathsf{Eq}$
defined in (8). In addition to the function
$\mathsf{Eq}$
defined in (8). In addition to the function
![]() $\mathsf{eqElim}$
in Example 2, we can also use the recursion rule for GADTs to define its companion function
$\mathsf{eqElim}$
in Example 2, we can also use the recursion rule for GADTs to define its companion function
Instantiating
![]() $\mathsf{a}$
and
$\mathsf{a}$
and
![]() $\mathsf{b}$
to the closed types
$\mathsf{b}$
to the closed types
![]() $\mathsf{a}_1$
and
$\mathsf{a}_1$
and
![]() $\mathsf{a}_2$
, respectively, the anonymous function
$\mathsf{a}_2$
, respectively, the anonymous function
reduces to the identity function on type
![]() $\mathsf{a}_1$
. By the uniqueness property of functions defined over GADTs given in (7),
$\mathsf{a}_1$
. By the uniqueness property of functions defined over GADTs given in (7),
reduces to the identity function on type
![]() $\mathsf{a}_1$
for any input
$\mathsf{a}_1$
for any input
![]() $\mathsf{p}$
. Semantically this entails that, if
$\mathsf{p}$
. Semantically this entails that, if
![]() $\varphi _a$
is the canonical isomorphism
$\varphi _a$
is the canonical isomorphism
![]() $a \simeq 1 \times a$
, and if
$a \simeq 1 \times a$
, and if
![]() $p : 1 \to [\![\mathsf{Eq\, a}_1 \mathsf{a}_2]\!]$
is any total function, then
$p : 1 \to [\![\mathsf{Eq\, a}_1 \mathsf{a}_2]\!]$
is any total function, then
Now, let
![]() $\mathsf{a}$
be a closed type and let
$\mathsf{a}$
be a closed type and let
![]() $\mathsf{t}$
be a terminating closed term of type
$\mathsf{t}$
be a terminating closed term of type
![]() $\mathsf{a}$
. We abuse notation and write
$\mathsf{a}$
. We abuse notation and write
![]() $[\![\mathsf{t}]\!] : 1 \to [\![\mathsf{a}]\!]$
for the total morphism
$[\![\mathsf{t}]\!] : 1 \to [\![\mathsf{a}]\!]$
for the total morphism
![]() $[\![\mathsf{\lambda \_ \to t}]\!]$
. Since every morphism with domain
$[\![\mathsf{\lambda \_ \to t}]\!]$
. Since every morphism with domain
![]() $1$
in
$1$
in
![]() $\mathscr{D}$
is a split monomorphism, so is
$\mathscr{D}$
is a split monomorphism, so is
![]() $[\![\mathsf{t}]\!]$
. Thus,
$[\![\mathsf{t}]\!]$
. Thus,
![]() $([\![\mathsf{t}]\!],{id}_1)$
is a split monomorphism as well. Moreover, since there is a functor
$([\![\mathsf{t}]\!],{id}_1)$
is a split monomorphism as well. Moreover, since there is a functor
![]() $[\![\mathsf{Eq}]\!] : \mathscr{C}^2 \to \mathscr{C}$
that manifests
$[\![\mathsf{Eq}]\!] : \mathscr{C}^2 \to \mathscr{C}$
that manifests
![]() $\mathsf{Eq}$
relative to
$\mathsf{Eq}$
relative to
![]() $[\![\_]\!]$
, and since split monomorphisms are preserved by all functors,
$[\![\_]\!]$
, and since split monomorphisms are preserved by all functors,
![]() $[\![\mathsf{Eq}]\!]([\![\mathsf{t}]\!],{id}_1)$
must also be a split monomorphism. By Lemma 12,
$[\![\mathsf{Eq}]\!]([\![\mathsf{t}]\!],{id}_1)$
must also be a split monomorphism. By Lemma 12,
![]() $[\![\mathsf{Eq}]\!]([\![\mathsf{t}]\!],{id}_1)$
is a total morphism from
$[\![\mathsf{Eq}]\!]([\![\mathsf{t}]\!],{id}_1)$
is a total morphism from
![]() $[\![\mathsf{Eq\, 1\, 1}]\!]$
to
$[\![\mathsf{Eq\, 1\, 1}]\!]$
to
![]() $[\![\mathsf{Eq\, a\, 1}]\!]$
. Consider the following morphisms:
$[\![\mathsf{Eq\, a\, 1}]\!]$
. Consider the following morphisms:
The observation at the end of the previous paragraph instantiated with
![]() $\mathsf{a}_1 = \mathsf{a}$
,
$\mathsf{a}_1 = \mathsf{a}$
,
![]() $\mathsf{a}_2 = \mathsf{1}$
, and
$\mathsf{a}_2 = \mathsf{1}$
, and
![]() $p$
being the total morphism
$p$
being the total morphism
![]() $[\![\mathsf{Eq}]\!]([\![ \mathsf{t}]\!],{id}_1) \circ [\![\mathsf{Refl}]\!]$
shows that
$[\![\mathsf{Eq}]\!]([\![ \mathsf{t}]\!],{id}_1) \circ [\![\mathsf{Refl}]\!]$
shows that
![]() $sr ={id}_{[\![\mathsf{a}]\!]}$
. The composition
$sr ={id}_{[\![\mathsf{a}]\!]}$
. The composition
![]() $rs$
is necessarily
$rs$
is necessarily
![]() ${id}_ 1$
because it is total and
${id}_ 1$
because it is total and
![]() $1$
is terminal in
$1$
is terminal in
![]() $\mathscr{D}$
. This explicitly gives that
$\mathscr{D}$
. This explicitly gives that
![]() $[\![\mathsf{a}]\!] \simeq 1$
, as announced in the statement of the theorem.
$[\![\mathsf{a}]\!] \simeq 1$
, as announced in the statement of the theorem.
7. Conclusion and Related Work
The first part of this paper shows that GADTs do not have satisfactory IAS as functors on
![]() $\mathit{Set}$
: the functorial completion semantics, which would give the smallest functorial IAS for them, do not have the expected parametricity properties so no others do either. Recognizing that the underlying reason for this is that GADTs’ map functions are inherently partial naturally led us to consider analogous semantics on
$\mathit{Set}$
: the functorial completion semantics, which would give the smallest functorial IAS for them, do not have the expected parametricity properties so no others do either. Recognizing that the underlying reason for this is that GADTs’ map functions are inherently partial naturally led us to consider analogous semantics on
![]() $\mathit{PSet}$
. But we have shown in the second part of the paper that, unfortunately, GADTs do not have IAS interpretations as functors on
$\mathit{PSet}$
. But we have shown in the second part of the paper that, unfortunately, GADTs do not have IAS interpretations as functors on
![]() $\mathit{PSet}$
either. These results show that if we hope to find IAS interpretations for GADTs as functors on some category, and if we hope that the resulting IAS will specialize to the standard one for ADTs and nested types, then we will have to look in categories far more esoteric than
$\mathit{PSet}$
either. These results show that if we hope to find IAS interpretations for GADTs as functors on some category, and if we hope that the resulting IAS will specialize to the standard one for ADTs and nested types, then we will have to look in categories far more esoteric than
![]() $\mathit{Set}$
and
$\mathit{Set}$
and
![]() $\mathit{PSet}$
.
$\mathit{PSet}$
.
The fundamental obstruction we have exposed in Section 6 is that GADTs’ map functions are partial in ways that are not compatible with composition. Indeed, as Theorem 18 shows, inconsistencies arise when a composition can be mapped over an element of a GADT even though the first function in the composition cannot. These kinds of pitfalls can be avoided either (i) by abandoning the partiality modeled by categories equipped with structures of computational partiality, or (ii) by abandoning the classical notion of functoriality. But (i) seems neither feasible nor desirable, since categories equipped with structures of computational partiality appear to capture exactly the computationally relevant notion of partiality it needs to. On the other hand, (ii) involves changing the notion of compositionality for GADTs’ map functions so that, in Theorem 18, a GADT’s interpretation needn’t send the composition of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
to the composition of their images under that interpretation. The challenge here is that if
$t_2$
to the composition of their images under that interpretation. The challenge here is that if
![]() $\mathsf{G}$
is an
$\mathsf{G}$
is an
![]() $n$
-ary GADT then the interpretation of
$n$
-ary GADT then the interpretation of
![]() $\mathsf{G}$
cannot simply be a functor. It must still have actions on objects and morphisms of
$\mathsf{G}$
cannot simply be a functor. It must still have actions on objects and morphisms of
![]() $\mathscr{C}^n$
like functors do, and must still send identities to identities, but it need not respect composition. Instead, the image of the composition of
$\mathscr{C}^n$
like functors do, and must still send identities to identities, but it need not respect composition. Instead, the image of the composition of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
under
$t_2$
under
![]() $\mathsf{G}$
’s interpretation must only be “more defined” than the composition of the images of
$\mathsf{G}$
’s interpretation must only be “more defined” than the composition of the images of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
under that interpretation. We will therefore consider, in future work, semantics in categories equipped with an ordering on morphisms and such that the interpretations of GADTs are normal lax functors instead of functors. Jay (Jay Reference Jay and Birtwistle1991) lays out the basic theory of such categories and lax functors that we plan to exploit to define the kind of semantics for GADTs we seek.
$t_2$
under that interpretation. We will therefore consider, in future work, semantics in categories equipped with an ordering on morphisms and such that the interpretations of GADTs are normal lax functors instead of functors. Jay (Jay Reference Jay and Birtwistle1991) lays out the basic theory of such categories and lax functors that we plan to exploit to define the kind of semantics for GADTs we seek.
There are treatments of GADTs beyond those discussed in the main body of this paper. Atkey’s parametric model for
![]() $F_\omega$
from (Atkey Reference Atkey, Cégielski and Durand2012) represents data types – including GADTs – as Church encodings. It requires the user to supply a map function for the (higher-order) type constructor whose fixpoint characterizes the data type. But, importantly, functoriality of an underlying type constructor does not imply functoriality of its fixpoint, so the data type itself still need not necessarily support a map function in Atkey’s model. Similarly, (Vytiniotis and Weirich Reference Vytiniotis and Weirich2010) present a parametric model for an extension of
$F_\omega$
from (Atkey Reference Atkey, Cégielski and Durand2012) represents data types – including GADTs – as Church encodings. It requires the user to supply a map function for the (higher-order) type constructor whose fixpoint characterizes the data type. But, importantly, functoriality of an underlying type constructor does not imply functoriality of its fixpoint, so the data type itself still need not necessarily support a map function in Atkey’s model. Similarly, (Vytiniotis and Weirich Reference Vytiniotis and Weirich2010) present a parametric model for an extension of
![]() $F_\omega$
that supports type equality and thus can encode GADTs, but this model still does not guarantee functoriality; accordingly, the parametric properties of GADTs described in the precursor work (Vytiniotis and Weirich Reference Vytiniotis and Weirich2006) to (Vytiniotis and Weirich Reference Vytiniotis and Weirich2010) are all inhabitation results rather than naturality results. In (Mandelbaum and Stump Reference Mandelbaum and Stump2009) GADTs are represented as Scott encodings rather than Church encodings but, again, only inhabitation results are cited for them. GADTs are treated explicitly as fixpoints of discrete functors in (Johann and Ghani Reference Johann and Ghani2008), as initial algebras of dependent polynomial functors in (Gambino and Hyland Reference Gambino, Hyland, Berardi, Coppo and Damiani2004; Hamana and Fiore Reference Hamana and Fiore2011), and as indexed containers in (Morris and Altenkirch Reference Morris and Altenkirch2009). The latter two treatments move toward seeing GADTs as data types in a dependent type theory. A categorical parametric model of dependent types has been given by (Atkey et al. Reference Atkey, Ghani and Johann2014), but, as with the models mentioned above, this model also does not guarantee that GADTs have functorial semantics.
$F_\omega$
that supports type equality and thus can encode GADTs, but this model still does not guarantee functoriality; accordingly, the parametric properties of GADTs described in the precursor work (Vytiniotis and Weirich Reference Vytiniotis and Weirich2006) to (Vytiniotis and Weirich Reference Vytiniotis and Weirich2010) are all inhabitation results rather than naturality results. In (Mandelbaum and Stump Reference Mandelbaum and Stump2009) GADTs are represented as Scott encodings rather than Church encodings but, again, only inhabitation results are cited for them. GADTs are treated explicitly as fixpoints of discrete functors in (Johann and Ghani Reference Johann and Ghani2008), as initial algebras of dependent polynomial functors in (Gambino and Hyland Reference Gambino, Hyland, Berardi, Coppo and Damiani2004; Hamana and Fiore Reference Hamana and Fiore2011), and as indexed containers in (Morris and Altenkirch Reference Morris and Altenkirch2009). The latter two treatments move toward seeing GADTs as data types in a dependent type theory. A categorical parametric model of dependent types has been given by (Atkey et al. Reference Atkey, Ghani and Johann2014), but, as with the models mentioned above, this model also does not guarantee that GADTs have functorial semantics.
Acknowledgment
This work was supported by National Science Foundation awards 1713389 and 2203217.