T₀-spaces and the lower topology

Abstract

The authors’ primary goal in this paper is to enhance the study of 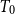$T_0$ topological spaces by using the order of specialization of a 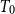$T_0$-space to introduce the lower topology (with a subbasis of closed sets 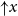$\mathord{\uparrow } x$) and studying the interaction of the original topology and the lower topology. Using the lower topology, one can define and study new properties of the original space that provide deeper insight into its structure. One focus of study is the property R, which asserts that if the intersection of a family of finitely generated sets $\mathord{\uparrow } F$, 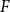$F$ finite, is contained in an open set 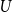$U$, then the same is true for finitely many of the family. We first show that property R is equivalent to several other interesting properties, for example, the property that all closed subsets of the original space are compact in the lower topology. We then find conditions under which these spaces are compact, well-filtered, and coherent, a weaker variant of stably compact spaces. We also investigate what have been called strong 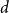$d$-spaces, develop some of their basic properties, and make connections with the earlier considerations involving spaces satisfying property R. Two key results we obtain are that if a dcpo 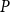$P$ with the Scott topology is a strong 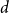$d$-space, then it is well-filtered, and if additionally the Scott topology of the product 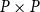$P\times P$ is the product of the Scott topologies of the factors, then the Scott space of 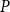$P$ is sober. We also exhibit connections of this work with de Groot duality.

1. Introduction

In his pioneering work in what has come to be called “domain theory,” which provides a mathematical foundation for the denotational semantics of programming languages, Dana Scott introduced a crucial $T_0$ -topology which came to be called the Scott topology. In domain theory and non-Hausdorff topology, we encounter numerous links between topology and order theory (cf. Abramsky and Jung 1994; Gierz et al. 2003; Goubault-Larrecq 2013). Sobriety is probably the most important and useful property of $T_0$ -spaces. The Hofmann-Mislove Theorem reveals a very distinct characterization for the sober spaces via open filters and illustrates the close relationship between domain theory and topology.

With the development of domain theory and non-Hausdorff topology, another two properties also emerged as the very useful and important properties for $T_0$ -spaces: the property of being a $d$ -space and the well-filteredness (see Gierz et al. 2003; Goubault-Larrecq 2013; Heckmann 1992; Jia 2018; Keimel and Lawson 2009; Wyler 1981; Xu et al. 2020b; Xu and Zhao 2021). In order to uncover more finer links between $d$ -spaces and well-filtered spaces, the notion of strong $d$ -spaces has been introduced in Xu and Zhao (2020).

It is worth noting that through other authors of Gierz et al. (2003), another topology was added in domain theory, the Lawson topology, which was the join of the Scott topology and a third topology, called the lower topology in Gierz et al. (2003) and other names elsewhere. The joining of the Scott and lower topology has proved a quite fruitful part of the overall theory and presented some important connections between domain theory and classical topology (which generally assumes the Hausdorff separation condition).

In this paper, we seek to extend this program to $T_0$ -spaces and explore much more general settings where one can fruitfully combine the study of a $T_0$ -space with the lower topology and the topology generated by the two together.

Taking a mildly different point of view, one can regard the investigation from the point of view of bitopological spaces, triples $(X,\tau, \nu )$ where $\tau$ and $\nu$ are topologies on $X$ and morphisms are maps that are continuous in both topologies. If one is considering $T_0$ -spaces, it is natural to consider order-dual topologies, topologies $\tau$ and $\nu$ for which the orders of specialization for $\tau$ and $\nu$ are opposites (see, e.g., Xu 2016b). In this setting, the join $\tau \bigvee \nu$ of the two topologies, the smallest topology containing both $\tau$ and $\nu$ , frequently plays an important role. From this viewpoint, we are looking at bitopological spaces $(X,\tau, \omega )$ , where $(X,\tau )$ is a $T_0$ -space and $\omega$ is the lower topology defined from the order of specialization of $(X,\tau )$ . We are interested in how these two topologies interact and focus primarily on the equivalent properties of $\Omega ^*$ -compactness (each $\tau$ -closed set is compact in the lower topology) and property $R$ (a kind of well-filtered property for the closed subsets of the lower topology). We also study strong $d$ -spaces and its relationship to the preceding notions and investigate the conditions under which the Scott topology on a dcpo is sober.

2. Preliminaries

In this section, we briefly recall some fundamental concepts and basic results about ordered structures and $T_0$ -spaces that will be used in the paper. For further details, we refer the reader to Gierz et al. (2003), Goubault-Larrecq (2013).

For a poset $P$ and $A\subseteq P$ , let $\mathord{\downarrow }A=\{x\in P: x\leq a \mbox{ for some } a\in A\}$ and $\mathord{\uparrow }A=\{x\in P: x\geq a \mbox{ for some } a\in A\}$ . For $x\in P$ , we write $\mathord{\downarrow }x$ for $\mathord{\downarrow }\{x\}$ and $\mathord{\uparrow }x$ for $\mathord{\uparrow }\{x\}$ . The set $A$ is called a lower set (resp., an upper set) if $A=\mathord{\downarrow }A$ (resp., $A=\mathord{\uparrow }A$ ). The family of all upper subsets of $P$ is denoted by $\mathbf{up}(P)$ . Let $P^{(\lt \omega )}=\{F\subseteq P : F\, \mbox{is a nonempty finite set}\}$ and $\mathbf{Fin} P=\{\uparrow F$ : $F\in P^{(\lt \omega )}\}$ . An upper set $B$ of $P$ is said to be finitely generated if there is $F\in P^{(\lt \omega )}$ such that $B=\mathord{\uparrow } F$ . For a nonempty subset $C$ of $P$ , define $\mathrm{max}(C)=\{c\in C : c\, \mbox{is a maximal element of}\, C\}$ and $\mathrm{min}(C)=\{c\in A : c\, \mbox{is a minimal element of}\, C\}$ .

For a set $X$ , let $|X|$ be the cardinality of $X$ and $2^X$ the set of all subsets of $X$ . The set of all natural numbers is denoted by $\mathbb{N}$ . When $\mathbb{N}$ is regarded as a poset (in fact, a chain), the order on $\mathbb{N}$ is the usual order of natural numbers. Let $\omega =|\mathbb{N}|$ .

A poset $P$ is called an inf semilattice (shortly a semilattice) if any two elements $a, b\in P$ have the greatest lower bound in $P$ , denoted by $a\wedge b$ . Dually, $P$ is a sup semilattice if any two elements $a, b\in P$ have the least upper bound in $P$ , denoted by $a\vee b$ . The poset $P$ is called sup complete, if every nonempty subset of $P$ has a sup (i.e., the least upper bound). In particular, a sup complete poset has a greatest element, the sup of $P$ . $P$ is called a complete lattice if every subset (including the empty set) has a sup and an inf. A totally ordered complete lattice is called a complete chain.

A nonempty subset $D$ of a poset $P$ is directed if every two elements in $D$ have an upper bound in $D$ . The set of all directed sets of $P$ is denoted by $\mathscr{D}(P)$ . The poset $P$ is called a directed complete poset, or dcpo for short, if for any $D\in \mathscr{D}(P)$ , $\bigvee D$ exists in $P$ . Clearly, a poset $Q$ is sup complete iff $Q$ is both a dcpo and a sup semilattice.

Lemma 1. Let $P$ be a poset and $D$ a countable directed subset of $P$ . Then there exists a countable chain $C\subseteq D$ such that $\mathord{\downarrow } D=\mathord{\downarrow } C$ . Hence, $\bigvee C$ exists and $\bigvee C=\bigvee D$ whenever $\bigvee D$ exists. If $D$ has no largest element, then $C$ can be chosen to be a strictly ascending chain.

Proof. If $|D|\lt \omega$ , then $D$ contains a largest element $d$ , so let $C=\{d\}$ , which satisfies the requirement.

Now assume $|D|=\omega$ and let $D=\{d_n:n\in \mathbb{N}\}$ . We use induction on $n\in \mathbb{N}$ to define $C=\{c_n:n\in \mathbb{N}\}$ . More precisely, let $c_1=d_1$ and let $c_{n+1}$ ( $n\in \mathbb{N}$ ) be an upper bound of $\{d_{n+1},c_0, c_1,c_2\ldots, c_n\}$ in $D$ . It is clear that $C$ is a chain and $\mathord{\downarrow } D=\mathord{\downarrow } C$ .

Suppose that $D=\{d_n:n\in \mathbb{N}\}$ is a countable directed and has no largest element. Let $c_1=d_1$ . Since $D$ has no largest element, there is $d_{m_1}\in D$ such that $d_{m_1}\not \leq c_1$ . Let $c_2$ be an upper bound of $\{d_2,c_1, d_{m_1}\}$ in $D$ . Then $c_1\lt c_2$ and $\{d_1, d_2\}\subseteq \downarrow c_2$ . We assume generally that for $n\in \mathbb{N}$ we have chosen in $D$ finite elements $c_i$ ( $1\leq i\leq n$ ) such that $ c_1\lt c_2\lt \ldots \lt c_n$ and $\{d_1, d_2, \ldots, d_n\}\subseteq \downarrow c_n$ . Then as $D$ has no largest element, there is $d_{m_n}\in D$ such that $d_{m_n}\not \leq c_n$ . Let $c_{n+1}$ be an upper bound of $\{d_{n+1},c_n, d_{m_n}\}$ in $D$ . Then $c_n\lt c_{n+1}$ and $\{d_1, d_2, \ldots, d_{n+1}\}\subseteq \downarrow c_{n+1}$ . So by induction we get a strictly ascending chain $C=\{c_n : n\in \mathbb{N}\}$ satisfying $\mathord{\downarrow } D=\mathord{\downarrow } C$ .

The category of all $T_0$ -spaces and continuous mappings is denoted by $\mathbf{Top}_0$ . For a $T_0$ -space $X$ , let $\mathscr{O}(X)$ (resp., $\mathscr{C}(X)$ ) be the set of all open subsets (resp., closed subsets) of $X$ . The closure of a subset $A$ in $X$ will be denoted by ${\textrm{cl}}_X A$ (or simply by ${\textrm{cl}} A$ if there is no ambiguity) or $\overline{A}$ , and the interior of $A$ will be denoted by ${\textrm{int}}_X A$ or simply by ${\textrm{int}} A$ . Let $\mathscr{D}_c(X)=\{\overline{D} : D\in \mathscr{D}(X)\}$ . We use $\leq _X$ to denote the specialization order of $X$ : $x\leq _X y$ iff $x\in \overline{\{y\}}$ . Clearly, all open sets (resp., closed sets) of $X$ are upper sets (resp., lower sets) of $X$ . A subset $B$ of $X$ is called saturated if $B$ equals the intersection of all open sets containing it (equivalently, $B$ is an upper set in the specialization order). For a poset $P$ , a $T_0$ -topology $\tau$ on $P$ is said to be order-compatible if $\leq _{(P, \tau )}$ (shortly $\leq _\tau$ ) agrees with the original order on $P$ .

In what follows, when a $T_0$ -space $X$ is considered as a poset, the order always refers to the specialization order if no other explanation is given. We will use $\Omega X$ or simply $X$ to denote the poset $(X, \leq _X)$ .

Definition 2. Let $P$ be a poset equipped with a topology. The partial order is said to be upper-semiclosed if each $\mathord{\uparrow } x$ is closed.

Definition 3. A topological space $X$ with a partial order is called upper-semicompact, if $\mathord{\uparrow } x$ is compact for any $x\in X$ , or equivalently, if $\mathord{\uparrow } x\cap A$ is compact for any $x\in X$ and $A\in \mathscr{C}(X)$ .

For a set $X$ and two topologies $\tau$ and $\nu$ on $X$ , the join $\tau \bigvee \nu$ is the topology generated by $\tau \bigcup \nu$ . It is the smallest topology on $X$ containing both $\tau$ and $\nu$ .

A subset $U$ of a poset $P$ is said to be Scott-open if (i) $U=\mathord{\uparrow }U$ , and (ii) for any directed subset $D$ with $\bigvee D$ existing, $\bigvee D\in U$ implies $D\cap U\neq \emptyset$ . All Scott-open subsets of $P$ form a topology, called the Scott topology on $P$ and denoted by $\sigma (P)$ . The space $\Sigma P=(P,\sigma (P))$ is called the Scott space of $P$ . A subset $C$ of $P$ is said to be Scott-compact if it is compact in $\Sigma P$ . For the chain $2 =\{0, 1\}$ (with the order $0\lt 1$ ), we have $\sigma (2)=\{\emptyset, \{1\}, \{0, 1\}\}$ . The space $\Sigma 2$ is well-known under the name of Sierpiński space.

The lower topology on $P$ , generated by $\{P\setminus \mathord{\uparrow } x : x\in P\}$ (as a subbase), is denoted by $\omega (P)$ . Dually, define the upper topology on $P$ (generated by $\{P\setminus \mathord{\downarrow } x : x\in P\}$ ) and denote it by $\upsilon (P)$ . The topology $\sigma (P)\bigvee \omega (P)$ is called the Lawson topology on $P$ and is denoted by $\lambda (P)$ . The collection of all upper sets of $P$ forms the (upper) Alexandroff topology $\alpha (P)$ . For a $T_0$ -topology $\tau$ on $P$ , it is easy to verify that $\tau$ is order-compatible iff $\upsilon (P) \subseteq \tau \subseteq \alpha (P)$ .

In the following, when a poset $P$ is considered as a $T_0$ -space, the topology on $P$ always refers to the Scott topology unless stated otherwise.

The following three results are well-known (see Gierz et al. 2003, Proposition II-2.1, Theorem III-1.9, and Proposition VI-1.6). The first is a key feature of the Scott topology.

Lemma 4. Let $P, Q$ be posets and $f : P \longrightarrow Q$ . Then the following two conditions are equivalent:

1. (1) $f$ is Scott continuous, that is, $f : \Sigma P \longrightarrow \Sigma Q$ is continuous.

2. (2) For any $D\in \mathscr{D}(P)$ for which $\bigvee D$ exists, $f(\bigvee D)=\bigvee f(D)$ .

Lemma 5. Let $X$ be a topological space with an upper-semiclosed partial order. If $A$ is a compact subset of $X$ , then $\mathord{\downarrow } A$ is Scott-closed.

Lemma 6. For a complete lattice $L$ , $(L, \lambda (L))$ is a compact $T_1$ -space.

Lemma 7. (Jia 2018 , Theorem 3.4) For a poset $P$ , $\Sigma P$ is compact iff $P$ is finitely generated.

Lemma 8. (Rudin’s Lemma) Let $P$ be a poset, $C$ a nonempty lower subset of $P$ , and $\mathscr{F} \subseteq \mathbf{Fin} P$ a filtered family. If $C$ meets all members of $\mathscr{F}$ , then $C$ contains a directed subset $D$ that still meets all members of $\mathscr{F}$ .

Rudin’s Lemma, given by Rudin (1981), is a useful tool in topology and plays a crucial role in domain theory (see Gierz et al. 1983, 2003; Goubault-Larrecq 2013). On some occasions, we only need the following consequence of Rudin’s Lemma.

Corollary 9. (Heckmann 1992, Lemma 2.4) Let $P$ be a dcpo, $U$ a nonempty Scott-open subset of $P$ and $\mathscr{F}\subseteq \mathbf{Fin} P$ a filtered family such that $\bigcap \mathscr{F}\subseteq U$ holds. Then $\mathord{\uparrow } F\subseteq U$ for some $\mathord{\uparrow } F\in \mathscr{F}$ .

Definition 10. A poset $P$ is said to be Noetherian if it satisfies the ascending chain condition (ACC for short): every ascending chain has a greatest member or, equivalently, every chain of $P$ has a largest member.

A $T_0$ -space $X$ is said to be hyper-sober if for any $F\in{\mathsf{Irr}} (X)$ , there is a unique $x\in F$ such that $F\subseteq{\textrm{cl}} \{x\}$ (cf. Zhao and Ho 2015).

Proposition 11. (Zhao and Ho 2015, Proposition 5.4 and Theorem 5.7) (Xu et al. 2020a, Proposition 3.8) For a poset $P$ , the following conditions are equivalent:

1. (1) $P$ is a Noetherian poset.

2. (2) Every directed subset of $P$ has a largest member.

3. (3) Every ideal of $P$ is principal.

4. (4) Every countable directed set of $P$ has a largest member.

5. (5) Every countable chain of $P$ has a largest member.

6. (6) Every countable ascending chain of $P$ has a largest member.

7. (7) $P$ is a dcpo and every element of $P$ is compact.

8. (8) $P$ is a dcpo and $\sigma (P)=\alpha (P)$ .

9. (9) The Alexandroff topology $\alpha (P)$ is sober.

10. (10) The Scott topology $\sigma (P)$ is hyper-sober.

Proposition 12. For a poset $P$ , the following two conditions are equivalent:

1. (1) $P$ is a Noetherian poset.

2. (2) $\mathbf{Fin} P$ (with the inverse inclusion order) is a Noetherian poset.

Proof. (1) $\Rightarrow$ (2): Let $P$ be a Noetherian poset. Then by Proposition 11, $P$ is a dcpo and $\sigma (P)=\alpha (P)$ . Hence by Proposition 3 of Xi and Zhao (2017) (see Lemma 24 below), $\mathord{\mathsf{K}} (\Sigma P)=\mathord{\mathsf{K}} ((P, \alpha (P))=\mathbf{Fin} P$ is a dcpo. Now we show that $\mathord{\uparrow } F\ll \mathord{\uparrow } F$ in $\mathbf{Fin} P$ for all $\mathord{\uparrow } F\in \mathbf{Fin} P$ . Suppose that $\{\mathord{\uparrow } F_d : d\in D\}\in \mathscr{D}(\mathbf{Fin} P)$ such that $\mathord{\uparrow } F \sqsubseteq \bigvee _{\mathbf{Fin} P}\{\mathord{\uparrow } F_d : d\in D\}$ . Then by Lemma 23 below, we have that $\bigcap _{d\in D}\mathord{\uparrow } F_d\subseteq \mathord{\uparrow } F\in \sigma (P)$ , whence by Corollary 9 there is $d\in D$ such that $\mathord{\uparrow } F_d\subseteq \mathord{\uparrow } F$ , that is $\mathord{\uparrow } F\sqsubseteq \mathord{\uparrow } F_d$ . Thus, $\mathord{\uparrow } F\ll _{\mathbf{Fin} P}\mathord{\uparrow } F$ . By Proposition 11, $\mathbf{Fin}P$ is a Noetherian poset.

(2) $\Rightarrow$ (1): Suppose that $\mathbf{Fin}P$ is a Noetherian poset and $D\in \mathscr{D}(P)$ . If $D$ has no largest element, the $\{\mathord{\uparrow } d : d\in D\}$ is a directed subset of $\mathbf{Fin}P$ having no largest member, which is a contradiction with the Noetherian property of $\mathbf{Fin}P$ . So $P$ is a Noetherian poset.

For the following definition and related conceptions, please refer to Abramsky and Jung (1994), Gierz et al. (2003), Goubault-Larrecq (2013).

Definition 13. For a dcpo $P$ and $A, B\subseteq P$ , we say $A$ is way below $B$ , written $A\ll B$ , if for each $D\in \mathscr{D}(P)$ , $\bigvee D\in \mathord{\uparrow } B$ implies $D\cap \mathord{\uparrow } A\neq \emptyset$ . For $B=\{x\}$ , a singleton, $A\ll B$ is written $A\ll x$ for short. For $x\in P$ , let $w(x)=\{F\in P^{(\lt \omega )} : F\ll x\}$ , $\Downarrow x = \{u\in P : u\ll x\}$ and $K(P)=\{k\in P : k\ll k\}$ . Points in $K(P)$ are called compact elements of $P$ .

Definition 14. Let $P$ be a dcpo and $X$ a $T_0$ -space.

1. (1) $P$ is called a continuous domain, if for each $x\in P$ , $\Downarrow x$ is directed and $x=\bigvee \Downarrow x$ .

2. (2) $P$ is called an algebraic domain, if for each $x\in P$ , $\downarrow x\cap K(P)$ is directed and $x=\bigvee (\downarrow x\cap K(P))$ .

3. (3) $P$ is called a quasicontinuous domain, if for each $x\in P$ , $\{\mathord{\uparrow } F : F\in w(x)\}$ is filtered and $\mathord{\uparrow } x=\bigcap \{\mathord{\uparrow } F : F\in w(x)\}$ .

4. (4) $X$ is called core-compact if $\mathscr{O}(X)$ is a continuous lattice.

It is well-known that every algebraic domain is a continuous domain and every continuous domain is a quasicontinuous domain but the converse implications do not hold in general (see Gierz et al. 1983, 2003).

For the concepts in the following definition, please refer to Erné (2018), Gierz et al. (2003), Heckmann (1992), Heckmann and Keimel (2013).

Definition 15. Let $X$ be a topological space and $S\subseteq X$ .

1. (1) $S$ is called strongly compact if for any open set $U$ with $S \subseteq U$ , there is a finite set $F$ with $S\subseteq \uparrow F \subseteq U$ .

2. (2) $S$ is called supercompact if for any family $\{U_i : i\in I\}\subseteq \mathscr{O}(X)$ , $S\subseteq \bigcup _{i\in I} U_i$ implies $S\subseteq U_i$ for some $i\in I$ .

3. (3) $X$ is called locally hypercompact if for each $x\in X$ and each open neighborhood $U$ of $x$ , there is a strongly compact set $S$ such that $x\in{\textrm{int}}\,\mathord{\uparrow } S\subseteq \mathord{\uparrow } S\subseteq U$ or, equivalently, there is $\mathord{\uparrow } F\in \mathbf{Fin}X$ such that $x\in{\textrm{int}}\,\mathord{\uparrow } F\subseteq \mathord{\uparrow } F\subseteq U$ .

4. (4) $X$ is called a $C$ -space if for each $x\in X$ and each open neighborhood $U$ of $x$ , there is a supercompact set $S$ such that $x\in{\textrm{int}}\,\mathord{\uparrow } S\subseteq \mathord{\uparrow } S\subseteq U$ or, equivalently, there is $u\in U$ such that $x\in{\textrm{int}}\,\mathord{\uparrow } u\subseteq \mathord{\uparrow } u\subseteq U$ .

The following result is well-known (see Gierz et al. 1983, 2003; Heckmann 1992).

Lemma 16. For a dcpo $P$ , the following three conditions are equivalent:

1. (1) $P$ is continuous (resp., quasicontinuous).

2. (2) $\Sigma P$ is a C-space (resp., a locally hypercompact space).

3. (3) For each $U\in \sigma (P)$ and $x\in U$ , there is $u\in U$ such that $x\in{\textrm{int}}\,\!_{\sigma (P)}\mathord{\uparrow } u\subseteq \mathord{\uparrow } u\subseteq U$ (resp., there is $\mathord{\uparrow } F\in \mathbf{Fin}X$ such that $x\in{\textrm{int}}\,\mathord{\uparrow } F\subseteq \mathord{\uparrow } F\subseteq U$ ).

Theorem 17. (Gierz et al. 2003 , Theorem II-4.13) Let $P$ be a poset. Then, the following statements are equivalent:

1. (1) $\Sigma P$ is core-compact (i.e., $\sigma (P)$ is a continuous lattice).

2. (2) For every poset $S$ one has $\Sigma (P\times S)=\Sigma P\times \Sigma S$ , that is, the Scott topology of $P\times S$ is equal to the product of the individual Scott topologies.

3. (3) For every dcpo or complete lattice $S$ one has $\Sigma (P\times S)=\Sigma P\times \Sigma S$ .

4. (4) $\Sigma (P\times \sigma (P))=\Sigma P\times \Sigma \sigma (P)$ .

Proof. It was proved in Gierz et al. (2003) for dcpos (see the proof of Gierz et al. 2003, Theorem II-4.13) and the proof is valid for posets.

Corollary 18. Suppose that $P$ is a poset for which $\Sigma P$ is locally compact. Then for every poset $S$ , $\Sigma (P\times S)=\Sigma P\times \Sigma S$ .

A $T_0$ -space $X$ is called a $d$ -space (or monotone convergence space) if $X$ (with the specialization order) is a dcpo and $\mathscr{O}(X) \subseteq \sigma (X)$ (cf. Gierz et al. 2003; Wyler 1981).

The $d$ -space has the following useful property.

Lemma 19. Let $X$ be a $d$ -space. Then for any nonempty closed set $A$ of $X$ , $A=\downarrow \mathrm{max}(A)$ , whence $\mathrm{max}(A)\neq \emptyset$ .

Proof. For $a\in A$ , by Zorn’s Lemma there is a maximal chain $C$ in $A$ with $a\in C$ . As $X$ is a $d$ -space, $c=\bigvee C$ exists in $X$ (with the specialization order) and $c\in A$ . Hence, $a\leq c\in \max (A)$ since $C$ is a maximal chain in $A$ with $a\in C$ . Therefore, $A=\downarrow \mathrm{max}(A)$ .

Proposition 20. For a $T_0$ -space $X$ , the following conditions are equivalent:

1. (1) $X$ is a $d$ -space.

2. (2) For any $D\in \mathscr{D}(X)$ and $U\in \mathscr{O}(X)$ , $\bigcap \limits \limits _{d\in D}\mathord{\uparrow } d\subseteq U$ implies $\mathord{\uparrow } d \subseteq U$ (i.e., $d\in U$ ) for some $d\in D$ .

3. (3) For any filtered family $\{\mathord{\uparrow }F_{i}:i\in I\}\subseteq \mathbf{Fin}X$ and any $U\in \mathscr{O}(X)$ , $\bigcap _{i\in I}\mathord{\uparrow }F_{i}\subseteq U$ implies $\mathord{\uparrow }F_{i}\subseteq U$ for some $i\in I$ .

Proof. (1) $\Leftrightarrow$ (2): See (Xu et al. 2020b, Proposition 3.3).

(3) $\Rightarrow$ (2): Trivial.

(1) $\Rightarrow$ (3): Let $U$ be an open subset of $X$ and $\mathscr{F}\subseteq \mathbf{Fin} X$ a filtered family such that $\bigcap \mathscr{F}\subseteq U$ holds. As $X$ is a $d$ -space, $X$ (with the specialization order)) is a dcpo and $U\in \sigma (X)$ . By Corollary 9, $\mathord{\uparrow }F_{i}\subseteq U$ for some $i\in I$ .

For a $T_0$ -space $X$ and a nonempty subset $A$ of $X$ , $A$ is irreducible if for any $\{F_1, F_2\}\subseteq \mathscr{C}(X)$ , $A \subseteq F_1\cup F_2$ implies $A \subseteq F_1$ or $A \subseteq F_2$ . Denote by ${\mathsf{Irr}}(X)$ (resp., ${\mathsf{Irr}}_c(X)$ ) the set of all irreducible (resp., irreducible closed) subsets of $X$ . Clearly, every subset of $X$ that is directed under $\leq _X$ is irreducible.

Remark 21. Let $X$ be a $T_0$ -space and $A$ a nonempty subset of $X$ . Then $A\in{\mathsf{Irr}} (X)$ iff for any $U, V\in \mathscr{O}(X)$ , $A\cap U\neq \emptyset$ and $A\cap V\neq \emptyset$ imply $A\cap U\cap V\neq \emptyset$ .

A topological space $X$ is called sober, if for any $A\in{\mathsf{Irr}}_c(X)$ , there is a unique point $x\in X$ such that $A=\overline{\{x\}}$ . It is straightforward to verify that every sober space is a $d$ -space (cf. Gierz et al. 2003). For simplicity, if a dcpo has a sober (resp., non-sober) Scott topology, then we will call $P$ a sober (resp., non-sober) dcpo.

The following result is well-known.

Proposition 22. (Gierz et al. 2003 , Proposition III-3.7) (Gierz et al. 1983 , Proposition 4.4) For a quasicontinuous domain (especially, a continuous domain) $P$ , $\Sigma \,\!\! P$ is sober.

For a $T_0$ -space $X$ , we shall use $\mathord{\mathsf{K}}(X)$ to denote the set of all nonempty compact saturated subsets of $X$ and endow it with the Smyth order $\sqsubseteq$ , that is, for $K_1,K_2\in \mathord{\mathsf{K}}(X)$ , $K_1\sqsubseteq K_2$ iff $K_2\subseteq K_1$ . Let $\mathscr{S}^u(X)=\{\mathord{\uparrow } x : x\in X\}$ and $\mathscr{S}^u_2(X)=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in X\}$ . Obviously, $\mathscr{S}^u(X)\subseteq \mathscr{S}^u_2(X)$ . The space $X$ is called well-filtered if it is $T_0$ , and for any open set $U$ and filtered family $\mathscr{K}\subseteq \mathord{\mathsf{K}}(X)$ , $\bigcap \mathscr{K}{\subseteq } U$ implies $K{\subseteq } U$ for some $K{\in }\mathscr{K}$ . It is called coherent if the intersection of any two compact saturated sets of $X$ is compact.

Lemma 23. (Xu et al. 2021 , Lemma 2.6) Let $X$ be a $T_0$ -space. For any nonempty family $\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$ , $\bigvee _{i\in I} K_i$ exists in $\mathord{\mathsf{K}} (X)$ iff $\bigcap _{i\in I} K_i\in \mathord{\mathsf{K}} (X)$ . In this case $\bigvee _{i\in I} K_i=\bigcap _{i\in I} K_i$ .

The following result is well-known (see, e.g., Xi and Zhao 2017, Proposition 3 or Xu et al. 2020b, Lemma 2.6).

Lemma 24. For a well-filtered space $X$ , $\mathord{\mathsf{K}} (X)$ is a dcpo.

For a dcpo with well-filtered Scott topology, Jia et al. (2018) gave the following useful characterization of coherence of its Scott space.

Lemma 25. (Jia 2018 , Lemma 3.1) Let $P$ be a dcpo for which $\Sigma P$ is well-filtered. Then the following three conditions are equivalent:

1. (1) $\Sigma P$ is coherent.

2. (2) $\mathord{\uparrow }x_{1}\cap \mathord{\uparrow }x_{2}\cap \ldots \cap \mathord{\uparrow }x_{n}$ is Scott-compact for all finite nonempty set $\{x_1, x_2, \ldots, x_n\}$ of $P$ .

3. (3) $\uparrow x \cap \uparrow y$ is Scott-compact for all $x, y\in P$ .

It is well-known that every sober space is well-filtered and every well-filtered space is a $d$ -space. Kou (2001) gave the first example of a dcpo whose Scott space is well-filtered but non-sober. Another simpler dcpo whose Scott topology is well-filtered but not sober was presented in Zhao et al. (2019). Jia (2018) constructed a countable infinite dcpo whose Scott topology is well-filtered but non-sober. It is worth noting that Johnstone (1981) constructed the first example of a dcpo whose Scott space is non-sober (indeed, it is not well-filtered) and Isbell (1982) constructed a complete lattice whose Scott space is non-sober. Xi and Lawson (2017) showed that every complete lattice is well-filtered in its Scott topology.

Proposition 26. (Xi and Lawson 2017, Proposition 2.4) Let $X$ be a $d$ -space such that $\downarrow (A\cap K)$ is closed for all $A\in \mathscr{C}(X)$ and $K\in \mathord{\mathsf{K}} (X)$ . Then $X$ is well-filtered.

Proposition 27. (Xi and Lawson 2017, Proposition 3.1 and Corollary 3.2) For a dcpo $P$ , if $(P, \lambda (P))$ is upper-semicompact (in particular, if $(P, \lambda (P))$ is compact or $P$ is a complete lattice), then $(P, \sigma (P))$ is well-filtered.

The following result is well-known (see Gierz et al. 2003, Kou 2001).

Theorem 28. For a $T_0$ -space $X$ , the following conditions are equivalent:

1. (1) $X$ is locally compact and sober.

2. (2) $X$ is locally compact and well-filtered.

3. (3) $X$ is core-compact and sober.

The above result was improved in Lawson et al. (2020) and Xu et al. (2020b) by two different methods.

Theorem 29. (Lawson et al. 2020 , Theorem 3.1) (Xu et al. 2020b, Theorem 6.16) Every core-compact well-filtered space is sober.

For any topological space $X$ , $\mathscr{G}\subseteq 2^{X}$ and $A\subseteq X$ , let $\Diamond _{\mathscr{G}} A=\{G\in \mathscr{G} : G\cap A\neq \emptyset \}$ and $\Box _{\mathscr{G}} A=\{G\in \mathscr{G} : G\subseteq A\}$ . The symbols $\Diamond _{\mathscr{G}} A$ and $\Box _{\mathscr{G}} A$ will be simply written as $\Diamond A$ and $\Box A$ respectively if there is no ambiguity. The upper Vietoris topology on $\mathscr{G}$ is the topology that has $\{\Box _{\mathscr{G}} U : U\in \mathscr{O}(X)\}$ as a base, and the resulting space is denoted by $P_S(\mathscr{G})$ .

The space $P_S(\mathord{\mathsf{K}}(X))$ , denoted briefly by $P_S(X)$ , is called the Smyth power space or upper space of $X$ (cf. Heckmann 1992; Schalk 1993). It is easy to verify that the specialization order of $P_S(X)$ is the Smyth order (i.e.,, $\leq _{P_S(X)}=\sqsupseteq$ ). The canonical mapping $\xi _X: X\longrightarrow P_S(X)$ , $x\mapsto \mathord{\uparrow } x$ , is a topological embedding (cf. Heckmann 1992; Heckmann and Keimel 2013; Schalk 1993).

3. Property R and $\Omega ^*$ -Compactness

In this section, we consider $T_0$ -spaces and posets equipped with the Scott topology and equip them also with the lower topology denoted by $\omega$ . We study in particular property R and the property of $\Omega ^*$ -compactness, the equivalence between them, and their main properties.

Definition 30. A $T_0$ -space $X$ is said to have property R if for any family $\{\mathord{\uparrow }F_{i}:i\in I\}\subseteq \mathbf{Fin} P$ and any $U\in \mathscr{O}(X)$ , $\bigcap _{i\in I}\mathord{\uparrow }F_{i}\subseteq U$ implies $\bigcap _{i\in I_{0}}\mathord{\uparrow }F_{i}\subseteq U$ for some $I_{0}\in I^{(\lt \omega )}$ . For a poset $P$ , when $\Sigma P$ has property R, we will simply say that $P$ has property R.

The property R was first introduced in Xu (2016a, Definition 10.2.11) (see also Wen and Xu 2018). Clearly, every $T_1$ -space has property R and the Sierpiński space $\Sigma 2$ has property R. We are particularly interested in the conditions under which a $T_0$ -space or a poset equipped with the Scott topology has property R.

We next recall the definition of $\Omega ^*$ -compactness from Lawson et al. (2020).

Definition 31. (Lawson et al. 2020 , Definition 5.1) A $T_0$ -space $X$ is said to be $\Omega ^{\ast }$ -compact if every closed subset of $X$ is compact in $(X, \omega (X))$ .

And lastly, we introduce a new concept.

Definition 32. A $T_0$ -space $X$ is well-filtered with respect to the family of $\omega$ -closed sets if any filtered family $\mathscr{D}$ of $\omega$ -closed sets has intersection contained in an open subset $U$ of $X$ , then some member of $\mathscr{D}$ is contained in $U$ . A poset $P$ has this property if the space $\Sigma$ P has it.

Proposition 33. Let $X$ be a $T_0$ -space.

1. (1) If $X$ is a $d$ -space and $\mathord{\uparrow } x\cap \mathord{\uparrow } y\in \mathbf{Fin} X\cup \{\emptyset \}$ for all $x, y\in X$ , then $X$ has property R

2. (2) If $X$ is well-filtered and $\bigcap _{u\in F}\mathord{\uparrow } u$ is compact for all $F\in P^{(\lt \omega )}$ (especially, if $X$ is well-filtered and coherent), then $X$ has property R.

Proof. We prove (1) and (2) in a uniform manner. Suppose that $\{x_{i}:i\in I\}\subseteq X$ and $U\in \mathscr{O}(X)$ such that $\bigcap _{i\in I}\mathord{\uparrow }x_{i}\subseteq U$ . For each $J\in I^{(\lt \omega )}$ , let $G_{J}=\bigcap _{i\in J}\mathord{\uparrow } x_{i}$ . If there is $J_0\in I^{(\lt \omega )}$ such that $G_{J_0}=\emptyset$ , then $\bigcap _{i\in J_0}\mathord{\uparrow } x_{i}\subseteq U$ . Now we assume that $G_{J}\neq \emptyset$ for all $J\in I^{(\lt \omega )}$ .

(1): Assume that $X$ is a $d$ -space and $\mathord{\uparrow } x\cap \mathord{\uparrow } y\in \mathbf{Fin} X\cup \{\emptyset \}$ for all $x, y\in X$ . Then $\{G_J : J\in I^{(\lt \omega )}\}\subseteq \mathbf{Fin} X$ and it is a filtered family. Since $X$ is a $d$ -space, $X$ (with the specialization order) is a dcpo and $U\in \mathscr{O}(X)\subseteq \sigma (X)$ . Clearly, $\bigcap _{J\in I^{(\lt \omega )}}G_J=\bigcap _{i\in I}\mathord{\uparrow }x_{i}\subseteq U$ . By Corollary 9, $G_J \subseteq U$ for some $J\in I^{(\lt \omega )}$ . Thus, $X$ has property R.

(2): Assume that $X$ is well-filtered and $\bigcap _{u\in F}\mathord{\uparrow } u$ is compact for all $F\in P^{(\lt \omega )}$ . Then $\{G_J : J\in I^{(\lt \omega )}\}$ is a filtered family of compact saturated subsets of $X$ and $\bigcap \limits _{J\in I^{(\lt \omega )}}G_J= \bigcap _{i\in I}\mathord{\uparrow }x_{i}\subseteq U$ . By the well-filteredness of $X$ , there is $J^{\prime }\in I^{(\lt \omega )}$ such that $\bigcap _{i\in J^{\prime }}\mathord{\uparrow } x_{i}=G_{J^{\prime }}\subseteq U$ , proving the property R of $X$ .

Corollary 34. For a $d$ -space $X$ , if $X$ (with the specialization order) is a sup semilattice (especially, $X$ is a complete lattice), then $X$ has property R. In particular, for any complete lattice $L$ , the Scott space $\Sigma L$ has property R.

In what follows, we will be working with the lattice of closed sets of the lower topology on a $T_0$ -space $X$ resp. poset $P$ , which we denote by $\omega ^*(X)$ resp. $\omega ^*(P)$ . The following is a key theorem.

Theorem 35. Let $X$ be a $T_0$ -space and $\mathscr{Q}=(\omega ^{*}(X),\supseteq )$ . Then the following conditions are equivalent:

1. (1) $X$ is well-filtered with respect to the family of $\omega$ -closed sets.

2. (2) $X$ satisfies property R.

3. (3) $X$ is $\Omega ^*$ -compact, that is all closed subspaces of $X$ are compact in the $\omega$ -topology.

4. (4) For any subset $S$ of $X$ and any open set $U$ , $\bigcap \{\mathord{\uparrow } x: x\in S\}\subseteq U$ implies there exists a finite subset $S_0$ of $S$ such that $\bigcap \{\mathord{\uparrow } x: x\in S_0\}\subseteq U$ .

5. (5) Every basic open set $\Box U$ in the upper Vietoris topology on $\omega ^*(X)$ belongs to the Scott topology of $Q$ .

Proof. (1) $\Rightarrow$ (2): Let $U$ be an open subset of $X$ and let $\{\mathord{\uparrow } F_{i}:i\in I\}\subseteq \mathbf{Fin} X$ satisfy

\begin{equation*} C:=\bigcap \{\mathord {\uparrow } F_i : i\in I\}\subseteq U .\end{equation*}

As $I_0$ varies over the finite subsets of $I$ , the sets $\bigcap _{i\in I_0} \uparrow F_i$ form a filtered family of closed sets in the $\omega$ -topology with intersection $C$ . By the hypothesized well-filtering property (1), one of these sets must be contained in $U$ , and thus property R holds.

(2) $\Rightarrow$ (1): Let $U$ be an open subset of $X$ and let $\mathscr{A}$ be a filtered family of sets closed in the $\omega$ -topology such that $\bigcap _{A\in \mathscr{A}} A\subseteq U$ . Consider the family

\begin{equation*} \mathscr {F}:= \{\mathord {\uparrow } F: \vert F\vert \lt \infty, \,A\subseteq \mathord {\uparrow } F \textrm { for some }A\in \mathscr {A}\}. \end{equation*}

Each $A\in \mathscr{A}$ is the intersection of members of $\mathscr{F}$ since the sets $\mathord{\uparrow } F$ , $F$ finite, form a basis for the closed sets of the $\omega$ -topology, and thus $\bigcap \mathscr{F}=\bigcap \mathscr{A}\subseteq U$ . By property R there exists finitely many members $\mathord{\uparrow } F_1,\ldots, \mathord{\uparrow } F_n$ of $\mathscr{F}$ such that $\bigcap _{i=1}^n \mathord{\uparrow } F_i\subseteq U$ . By choice of the $F_i$ we may pick for each $i$ some $A_i\in \mathscr{A}$ such that $A_i\subseteq \mathord{\uparrow } F_i$ . By the filteredness of $\mathscr{A}$ , we may pick $A\in \mathscr{A}$ such that $A\subseteq \bigcap _{i=1}^n A_i$ . Then $A\subseteq U$ , and hence the well-filtering property is established.

(2) $\Leftrightarrow$ (3): The complements of the sets $\mathord{\uparrow } F$ , $F$ finite, form a basis for the $\omega$ -topology. By taking compliments, we can read property R to say any open cover of a closed set $A=X\setminus U$ by such basic open sets has a finite subcover. Equivalently by the Alexander Subbasis Theorem, the closed set $A$ is compact in the $\omega$ -topology.

(2) $\Leftrightarrow$ (4): The property of (4) is essentially property R restricted to sets of the form $\mathord{\uparrow } x$ instead of $\mathord{\uparrow } F$ , $F$ finite. These sets form a subbasis for the $\omega$ -closed sets, so the proof follows along the lines of (2) $\Leftrightarrow$ (3).

(1) $\Rightarrow$ (5): It follows directly from (1) that any basic open set $\Box U$ in the upper Vietoris topology on $\omega ^*(X)$ is Scott-open in the lattice $\mathscr{Q}$ .

(5) $\Rightarrow$ (2): It is straightforward to deduce property R from the hypothesis that each $\Box U$ is Scott-open in the lattice $\mathscr{Q}$ .

We can enhance the preceding slightly if we are working with dcpos equipped with the Scott topology.

Corollary 36. A dcpo $L$ endowed with the Scott topology satisfies any $($ and hence all $)$ of the preceding five properties if and only if the Scott-closed sets of $L$ are precisely the saturated compact sets for the lower topology.

Proof. Assume $L$ is $\Omega ^*$ -compact. Then, the Scott-closed sets are compact with respect to the lower topology and they are saturated since that are lower sets. Conversely let $A=\mathord{\downarrow } A$ be $\omega$ -compact. Let $D$ be a directed subset of $A$ with supremum $e$ . Then, $\{\mathord{\uparrow } d: d\in D\}$ is a filtered family of $\omega$ -closed sets each of which meets the $\omega$ -compact set $A$ , and hence, their intersection must contain some $y\in A$ , which must be an upper bound for $D$ . Thus, $\sup D\leq y\in A=\mathord{\downarrow } A$ . Thus, $\sup D\in A$ , and we see that $A$ is Scott-closed.

Recall that for a topological space $(X, \tau )$ , the de Groot dual $\tau ^d$ of $\tau$ is defined by taking as a subbasis for the closed sets all compact saturated sets in $(X, \tau )$ . The patch topology $\tau ^{\sharp }$ on $X$ is the coarsest topology that is finer than the original topology $\tau$ and its de Groot dual $\tau ^d$ , namely, $\tau ^{\sharp }=\tau \bigvee \tau ^d$ .

Remark 37. The preceding corollary shows for a dcpo $L$ equipped with Scott topology and satisfying any of the conditions of Theorem 35 that $\omega (L)^d=\sigma (L)$ and hence $\lambda (L)=\omega (L)^{\sharp }$ .

See Example 56 of the next section for an example of the Scott space of a dcpo (indeed an algebraic domain) that does not satisfy property R (and hence the equivalent properties).

Remark 38. It will be convenient to have a short name for the $T_0$ -spaces that satisfy the previous five equivalent properties. For the purposes of this paper, we refer to them as $R$ -spaces. Let $\mathbf{Top}_r$ denote the category of all R-spaces and continuous mappings.

The following corollary follows directly from Proposition 20 and the Theorem35(4) by taking directed sets for $S$ .

Corollary 39. An $R$ -space is a $d$ -space.

A significant question in the study of $T_0$ -spaces equipped with the lower topology is the identification of useful conditions for the Lawson topology induced by the given topology, the topology generated by the given topology and the lower topology, to be compact. Using property R we can specify necessary and sufficient conditions.

Proposition 40. For a $T_0$ -space $X$ , the following are equivalent:

1. (1) The joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is compact.

2. (2) $X$ is a compact $R$ -space and $\bigcap \{\mathord{\uparrow } x: x\in F\}$ is compact for all finite subsets $F$ of $X$ .

Proof. (1) $\Rightarrow$ (2): As the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is compact, $X$ is a compact space. Each $\bigcap \{\mathord{\uparrow } x: x\in F\}$ for $F$ finite is closed in the lower topology, hence closed in the join $\mathscr{O}(X)\bigvee \omega (X)$ and thus compact in $\mathscr{O}(X)\bigvee \omega (X)$ since the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is compact by hypothesis. But then it is certainly compact in the weaker topology of $X$ . Every closed subset $A$ of $X$ in its given topology is closed in $\mathscr{O}(X)\bigvee \omega (X)$ , whence compact in $\mathscr{O}(X)\bigvee \omega (X)$ , and hence compact in the lower topology. Thus, $X$ is $\Omega ^*$ -compact and hence satisfies the equivalent property R by Theorem35.

(2) $\Rightarrow$ (1): We assume $X$ is covered by an open covering from the subbasis consisting of sets open in $X$ and sets $X\setminus \mathord{\uparrow } x$ for $x\in X$ . Let $S$ be the set of $x$ such that $X\setminus \mathord{\uparrow } x$ is in the cover and $\mathscr{U}$ the family of sets $U$ in the cover with $U\not \in \{X\setminus \mathord{\uparrow } x : x\in S\}$ . If $S$ is empty, then $\mathscr{U}$ is an open cover of $X$ . As $X$ is compact, there is a finite subcover $\mathscr{U}_0$ . If $\mathscr{U}$ is empty, then the family $\{X\setminus \mathord{\uparrow } x: x\in S\}$ is a lower-open cover $X$ , whence $\bigcap \{\mathord{\uparrow } x:x\in S\}=\emptyset$ . By Theorem35(4) (with $U=\emptyset$ ) there exists a finite subset $S_0$ of $S$ such that $\bigcap \{\mathord{\uparrow } x:x\in S_0\}=\emptyset$ . Then $\{X\setminus \mathord{\uparrow } x: x\in S_0\}$ is a finite subcover of $X$ .

In the remaining case, let $A=\bigcap \{\mathord{\uparrow } x:x\in S\}$ , a nonempty set. Then, the union $U$ of all the sets in $\mathscr{U}$ is an open set containing $A$ . Again from Theorem35(4) there exist a finite subset $S_0$ of $S$ such that $F=\bigcap \{\mathord{\uparrow } x:x\in S_0\}\subseteq U$ . By hypothesis $F$ is compact in $X$ , so finitely many of the open sets in $\mathscr{U}$ must cover $F$ . These finitely many open sets combined with $\{X\setminus \mathord{\uparrow } x:x\in S_0\}$ are then a finite subcover of the original cover. By the Alexander Subbasis Theorem $X$ is compact in the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ .

Example 41. Construct a Noetherian poset $P$ by taking an infinite antichain $A$ and attaching two incomparable lower bounds $y,z$ to $A$ and equipping it with the Scott topology, which is the Alexandroff discrete topology. Clearly, $\Sigma P$ is compact and satisfies Theorem 35 (4) since any subset of $S$ of cardinality greater than 3 has no upper bound, and hence, is an R-space. However, $\mathord{\uparrow } y\cap \mathord{\uparrow } z$ is not Scott-compact, and the joint topology $\sigma (P)\bigvee \omega )P)$ (i.e., the Lawson topology) on $P$ is discrete and hence noncompact.

We can modify the preceding ideas to derive a sufficient condition for a space to be an R-space.

Proposition 42. Let $X$ be a $T_0$ -space for which the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is compact when restricted to any $\mathord{\uparrow } x$ . Then $X$ is an R-space.

Proof. Suppose that $\{\mathord{\uparrow }F_{j}:j\in J\}\subseteq \mathbf{Fin} X$ and $U$ is an open subset of $X$ with $\bigcap _{j\in J}\mathord{\uparrow }F_{j}\subseteq U$ . Select an $j_0\in J$ . Then $\uparrow F_{j_0}\subseteq U\cup \bigcup _{j\in J\setminus \{j_0\}}( x\setminus \mathord{\uparrow }F_{j})$ . As the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ restricted to each $\mathord{\uparrow } x$ is compact and $F_{j_0}$ is finite, $\uparrow F_{j_0}$ is compact in $(X, \mathscr{O}(X)\bigvee \omega (X))$ , whence there exists $J_{0}\in (J\setminus \{j_0\})^{(\lt \omega )}$ such that $\uparrow F_{j_0}\subseteq U\cup \bigcup _{j\in J_0}(X\setminus \mathord{\uparrow }F_{j})$ or, equivalently, $\bigcap _{j\in J_{0}\cup \{j_o\}}\mathord{\uparrow }F_{j}\subseteq U$ . Thus, $X$ is an R-space.

We recall a result important for our purposes from Lawson et al. (2020, Theorem 7.1).

Theorem 43. If the Scott space $\Sigma P$ for a dcpo $P$ is $\Omega ^*$ -compact (i.e., $\Sigma P$ is an R-space), then it is well-filtered.

From the preceding Lemma 25 and Jia et al. (2018, Theorem 3.4), we derive the following equivalences.

Theorem 44. Let $L$ be a dcpo equipped with the Scott topology. Then the following conditions are equivalent:

1. (1) $L$ is a compact, $\Omega ^*$ -compact (i.e., $\Sigma L$ is a compact R-space), and $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is compact for each $x,y\in L$ .

2. (2) $L$ is compact, well-filtered, and $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is compact for each $x,y\in L$ .

3. (3) $L$ is finitely generated, well-filtered, and coherent.

4. (4) $L$ is well-filtered and patch-compact (i.e., $L$ is compact in the patch topology $\sigma (L)^{\sharp }$ ).

5. (5) $L$ is well-filtered and Lawson-compact.

6. (6) $L$ is patch-compact.

7. (7) $L$ is Lawson-compact.

Proof. Items (2) through (5) are shown to be equivalent in Jia et al. (2018, Theorem 3.4).

(1) $\Rightarrow$ (2): Follows directly from Theorem43.

(5) $\Rightarrow$ (7): Trivial.

(6) $\Rightarrow$ (7): Since the patch topology $\sigma (L)^{\sharp }$ is finer than the Lawson topology $\lambda (L)$ .

(7) $\Rightarrow$ (1): By Proposition 40 (for $X=\Sigma L$ ).

Remark 45. By Lemma 7, the conditions of $L$ being compact and being finitely generated are interchangeable in the various conditions of Theorem 44 .

Now we turn to locally hypercompact spaces (see Definition 15), also called locally finitary compact spaces (Goubault-Larrecq 2013, Exercise 5.1.42) or $qc$ -spaces.

Lemma 46. Let $(X,\tau )$ be a locally hypercompact space. Then

1. (1) Every compact saturated set is closed in the $\omega$ -topology.

2. (2) The order of specialization is a closed order in the product space $(X, \mathscr{O}(X)\bigvee \omega (X))\times (X, \mathscr{O}(X)\bigvee \omega (X))$ . In particular, the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is Hausdorff.

Proof. (1): Let $K$ be a compact saturated set and let $U$ be an open set containing $K$ . By local hypercompactness, we can choose for each $x\in K$ a finite set $F_x$ such that $x\in \mathrm{int}\mathord{\uparrow } F_x\subseteq \mathord{\uparrow } F_x\subseteq U$ . By the compactness of $K$ , there is a finite set $\{x_1, x_2, \ldots, x_n\}$ of $K$ such that $K\subseteq \bigcup _{i=1}^n \mathrm{int}\mathord{\uparrow } F_{x_i}$ . Let $F=\bigcup _{i=1}^n \mathord{\uparrow } F_{x_i}$ . Then $\mathord{\uparrow } F$ is an $\omega$ -closed set containing $K$ and contained in $U$ . By saturation of $K$ , it is the intersection of all such $U$ , thus the intersection of the finitely generated upper sets just constructed for each $U$ .

(2): Assume that $x\not \leq y$ . Then there exists a finite set $F\subseteq X\setminus \mathord{\downarrow } y$ and a $\tau$ -open set $V$ such that $x\in V\subseteq \mathord{\uparrow } F$ . Then $V\times (X\setminus \mathord{\uparrow } F)$ is an open set in the product space $(X, \mathscr{O}(X)\bigvee \omega (X))\times (X, \mathscr{O}(X)\bigvee \omega (X))$ that misses the graph $\{(u,v)\in X\times X: u\leq v\}$ of the order of specialization. We conclude that $\leq$ and $\geq$ are closed in the product space $(X, \mathscr{O}(X)\bigvee \omega (X))\times (X, \mathscr{O}(X)\bigvee \omega (X))$ . Then the diagonal $\leq \cap \geq$ is also closed, so $X$ with the joint topology $\mathscr{O}(X)\bigvee \omega (X)$ is Hausdorff.

We refer the reader to Lawson (1998) for results related to the previous lemma and following proposition.

Proposition 47. Let $P$ be a quasicontinuous domain for which the Scott space $(P,\sigma (P))$ is an R-space. Then $(P,\sigma (P))$ and $(P,\omega (P))$ are de Groot duals of each other.

Proof. By Lemma 16 $\Sigma X$ is a locally hypercompact space. So by Lemma 46(1) the de Groot dual topology of $\sigma (P)$ is contained in the lower topology. Since each $\mathord{\uparrow } x$ is compact in the Scott topology, it is closed in the de Groot dual topology, and hence the lower topology is contained in the de Groot dual topology since the sets $\mathord{\uparrow } x$ form a subbasis for the closed sets.

Since the Scott space $(P,\sigma (P))$ is an R-space, by Corollary 36 the de Groot dual of the lower topology of $P$ is the Scott topology of $P$ .

Example 48. Let $P$ be the negative integers (equipped with the usual order of integers) with two incomparable lower bounds $\bot _0$ and $\bot _1$ adjoined. Then $P$ is Noetherian, hence an algebraic domain with all elements compact, in particular a quasicontinuous domain. All order consistent and dual order consistent topologies collapse to all upper sets and all lower sets respectively, more precisely, $\upsilon (P)=\alpha (P)$ and $\omega (P)=\alpha (P^{op})$ . Clearly, both the (upper) Alexandroff topology $\alpha (P)$ and the (lower) Alexandroff topology $\alpha (P^{op})$ are compact. So both $(P, \omega (P))$ and $\Sigma P$ are compact R-spaces, whence the conditions of Proposition 47 are satisfied, and hence $\sigma (P)^{\sharp }=\omega (P)^{\sharp }=\sigma (P)\bigvee \omega (P)=\lambda (P)$ . Since $P$ is Noetherian and the dual poset $P^{op}$ of $P$ is not a dcpo, $\Sigma P$ is sober and $(P, \omega (P))$ is not a $d$ -space (and hence not well-filtered). Clearly, $\mathsf{K}((P, \omega (P))=\{\mathord{\downarrow } A : \emptyset \neq A\subseteq P\}$ . So $((P, \omega (P))$ is coherent, but $((P, \sigma (P))$ is not coherent since $\mathord{\uparrow } \bot _0\cap \mathord{\uparrow } \bot _1$ is not Scott-compact. The Lawson topology $\lambda (P)$ is discrete and hence noncompact.

4. Strong $\textit{d}$ -Spaces

As a strengthened version of $d$ -spaces, the notion of strong $d$ -spaces was introduced in Xu and Zhao (2020). In this section, we will give some characterizations of strong $d$ -spaces. These characterizations indicate that the notion of a strong $d$ -space is, in some sense, a variant of join continuity. We also find conditions on a $d$ -space $X$ under which $X$ is sober. In particular, we show that for a dcpo $P$ , if $\Sigma P$ is a strong $d$ -space and $\Sigma (P\times P)=\Sigma P\times \Sigma P$ , then $\Sigma P$ is sober.

Definition 49. (Xu and Zhao 2020, Definition 3.18) A $T_0$ -space $X$ is called a strong $d$ -space if for any $D\in \mathscr{D}(X)$ , $x\in X$ and $U\in \mathscr{O}(X)$ , $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ implies $\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ for some $d\in D$ . The category of all strong $d$ -spaces and continuous mappings is denoted by $\mathbf{S}$ - $\mathbf{Top}_d$ .

We list some elementary properties of strong $d$ -spaces.

Lemma 50. Let $X$ be a $T_0$ -space.

1. (1) If $X$ is a strong $d$ -space, then it is a $d$ -space.

2. (2) If $X$ is a strong $d$ -space, $D$ is directed, $A$ is closed, and $\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A\neq \emptyset$ for all $d\in D$ , then $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A\neq \emptyset$ .

3. (3) If $X$ is an R-space, then $X$ is a strong $d$ -space.

Proof. (1): Suppose that $D\in \mathscr{D}(X)$ and $U\in \mathscr{O}(X)$ with $\bigcap \limits \limits _{d\in D}\mathord{\uparrow } d\subseteq U$ . Select any $x\in D$ . Then $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x=\bigcap _{d\in D}\mathord{\uparrow } d\subseteq U$ . As $X$ is a strong $d$ -space, there exists $d_0\in \overline{D}$ such that $\mathord{\uparrow } d_0\cap \mathord{\uparrow } x\subseteq U$ . By the directedness of $D$ , there is $d\in D$ with $d_0\leq d$ and $x\leq d$ . Then $\mathord{\uparrow } d\subseteq \mathord{\uparrow } d_0\cap \mathord{\uparrow } x\subseteq U$ . By Proposition 20 $X$ is a $d$ -space.

(2): Follows immediately from the definition by taking $U=X\setminus A$ .

(3): Suppose $\bigcap \{\mathord{\uparrow } x\cap \mathord{\uparrow } d: d\in D\}\subseteq U$ , where $D$ is a directed set and $U$ is open. Setting $S=D\cup \{x\}$ and applying Theorem35(4), we conclude there exists a finite subset $S_0$ such that $\bigcap \{\mathord{\uparrow } q : q\in S_0\}\subseteq U$ . Then $\bigcap _{d\in S_0\setminus \{x\}}\mathord{\uparrow } d\cap \mathord{\uparrow } x \subseteq U$ . Hence, $X$ is a strong $d$ -space.

Fig. 1 shows certain relations of some spaces lying between $d$ -spaces and $T_2$ -spaces (all implications in Fig. 1 are irreversible).

Figure 1. Relations of some spaces lying between $d$ -spaces and $T_2$ spaces.

In Li et al. (2023, Example 5.2), a poset $P$ was given to show that $P$ equipped with a certain topology $\tau$ is a strong $d$ -space but the product space $(P, \tau )\times (P, \tau )$ is not a strong $d$ -space (and hence the category $\mathbf{S}$ - $\mathbf{Top}_d$ is not a reflective subcategory of $\mathbf{Top}_0$ ). Using this space we will show that the product of two R-spaces is not an R-space in general.

Example 51. Let $P=\mathbb{N}\cup \{\omega \}\cup \{\beta _1, \beta _2, \ldots, \beta _n, \ldots \}\cup \{a_1, a_2, \ldots, a_n, \ldots \}\cup \{a\}$ . Define an order on $P$ as follows (see Fig. 2 ):

1. (i) $1\lt 2\lt 3\lt \ldots \lt n\lt n+1\lt \omega \textrm{ for all }n\in \mathbf{N}$ ;

2. (ii) $\omega \lt \beta _n \textrm{ for all }n\in \mathbf{N}$ ;

3. (iii) $n\lt a_m \textrm{ iff }n\leq m$ ;

4. (iv) $a\lt \beta _n \textrm{ and } a\lt a_n \textrm{ for all }n\in \mathbf{N}$ .

Figure 2. The poset $P$ in Example 51.

Let $B=\{\beta _1, \beta _2, \ldots, \beta _n, \ldots \}$ and $A=\{a_1, a_2, \ldots, a_n, \ldots \}$ , and let $\tau _1=\{U\in \sigma (P) : A\setminus U \textrm{ is finite} \}$ and $\tau _2=\{U\in \sigma (P) : U\subseteq A\}$ . Define $\tau =\tau _1\bigcup \tau _2$ . Then

1. (a) $\textrm{max}(P)=A\cup B$ .

2. (b) $D\in \mathscr{D}(P)$ iff $D\subseteq \mathbb{N}$ is an infinite chain or $D$ has a largest element. So $P$ is a dcpo. If $D\subseteq \mathbb{N}$ is an infinite chain or $D$ has a largest element, then $D\in \mathscr{D}(P)$ . Conversely, suppose that $D$ is a directed subset of $P$ and $D$ has no largest element. Then $D$ is countably infinite and $|D\cap \textrm{max}(P)|\lt 2$ . If there exists $d^{\ast }\in D$ with $d^{\ast }\in \textrm{max}(P)$ , then for any $d\in D$ , by the directedness of $D$ , there is $d^{\prime }\in D$ such that $d\leq d^{\prime }$ and $d^{\ast }\leq d^{\prime }$ . Then $d\leq d^{\prime }=d^{\ast }$ . So $d^{\ast }$ is the largest element of $D$ , a contradiction. Hence, $D\cap \textrm{max}(P)=\emptyset$ , that is, $D\subseteq \mathord{\downarrow } \omega \cup \{a\}$ . Since for any $s\in \mathord{\downarrow } \omega$ , $s$ and $a$ have no upper bound in $D$ , we have $a\not \in D$ , and hence, $D\subseteq \mathord{\downarrow } \omega$ . As $D$ has no largest element, $D\subseteq \mathbb{N}$ is an infinite chain.

3. (c) $P$ is an algebraic domain. By (b), $x\ll x$ for all $x\in P\setminus \{\omega \}$ . Hence, $P$ is an algebraic domain.

4. (d) $\Sigma P$ is sober, not a strong $d$ -space and not coherent. By (c) and Proposition 22, $\Sigma P$ is sober. We have that $\bigcap _{n\in \mathbb{N}}\mathord{\uparrow } n\cap \mathord{\uparrow } a=\{\beta _1, \beta _2, \ldots, \beta _n, \ldots \}\in \sigma (P)$ , but $\mathord{\uparrow } m\cap \mathord{\uparrow } a=\{\beta _1, \beta _2, \ldots, \beta _n, \ldots \}\cup \{a_m, a_{m+1}, \ldots \}\not \subseteq \{\beta _1, \beta _2, \ldots, \beta _n, \ldots \}$ for any $m\in \mathbb{N}$ . Hence, $\Sigma P$ is not a strong $d$ -space. Clearly, $\mathord{\uparrow } 1, \mathord{\uparrow } a\in \mathord{\mathsf{K}} (\Sigma P)$ , but $\mathord{\uparrow } 1\cap \mathord{\uparrow } a=A\cup B$ is not Scott-compact (note that $\{\beta _n\}, \{a_n\}\in \sigma (P)$ for any $n\in \mathbb{N}$ ). So $\Sigma P$ is not coherent.

5. (e) $\tau$ is a topology on $P$ and $\upsilon (P)\subseteq \tau \subseteq \sigma (P)$ . Hence, $\tau$ is an order-compatible topology of $P$ and $(P, \tau ))$ is a $d$ -space. It was showed in (Li et al., 2023, Example 5.2).

6. (f) $(P, \tau )$ is sober and not coherent. Suppose that $C\in{\mathsf{Irr}}_c((P, \tau ))$ . Then by (e) and Lemma 19, $C=\mathord{\downarrow } \textrm{max}(P)$ . We claim that $\textrm{max}(C)$ is finite. Assume, on the contrary, that $\textrm{max}(C)$ is (countably) infinite. Since $C$ is Scott-closed and $\omega =\bigvee \mathbb{N}$ , $\textrm{max}(C)\cap (\mathord{\downarrow } \omega \cup \{a\})$ is a finite set, and consequently, $\textrm{max}(C)\cap \textrm{max}(P)$ is infinite.

   Case 1: $|\textrm{max}(C)\cap A|\geq 2$ . Select any $a_l, a_k\in \textrm{max}(C)\cap A$ with $a_l\neq a_k$ . Let $U_1=\{a_l\}$ and $U_2=\{a_k\}$ . Then $U_1, U_2\in \tau _2\subseteq \tau$ , $a_l\in C\cap U_1$ and $a_k\in C\cap U_2$ . But $A\cap U_1\cap U_2=\emptyset$ , which is a contradiction with $C\in{\mathsf{Irr}}_c((P, \tau ))$ .

   Case 2: $|\textrm{max}(C)\cap A|\lt 2$ . As $\textrm{max}(C)\cap \textrm{max}(P)=(\textrm{max}(C)\cap A)\cup (\textrm{max}(C)\cap B)$ is infinite, $\textrm{max}(C)\cap B$ must be infinite. Select any $\beta _n, \beta _m\in \textrm{max}(C)\cap B$ with $\beta _n\neq \beta _m$ . Let $V_1=\{\beta _n\}\cup (A\setminus \textrm{max}(C)\cap A)$ and $V_2=\{\beta _m\}\cup (A\setminus \textrm{max}(C)\cap A)$ . Then $V_1, V_2\in \tau _1\subseteq \tau$ , $\beta _n\in C\cap V_1$ and $\beta _m\in C\cap V_2$ . But $A\cap V_1\cap V_2=\emptyset$ , which is in contradiction with $C\in{\mathsf{Irr}}_c((P, \tau ))$ . Hence, $\textrm{max}(C)=\{x_1, x_2, x_3, \ldots, x_n\}$ is finite, then $C=\mathord{\downarrow } \textrm{max}(C)=\bigcup \limits _{i=1}^n\mathord{\downarrow } x_i$ and hence $C=\mathord{\downarrow } x_m={\textrm{cl}}_{\tau }\{x_m\}$ for some $1\leq m\leq n$ by $C\in{\mathsf{Irr}}_c((P, \tau ))$ . Thus, $(P, \tau ))$ is sober. Clearly, $\mathord{\uparrow } 1, \mathord{\uparrow } a\in \mathord{\mathsf{K}} (\Sigma P)$ , but $\mathord{\uparrow } 1\cap \mathord{\uparrow } a=A\cup B$ is not compact (note that $\{\{\beta _n\}\cup A : n\in \mathbb{N}\}$ is a $\tau$ -open cover of $A\cup B$ containing no finite subcover). Therefore, $(P, \tau ))$ is not coherent.

7. (g) $(P, \tau ))$ is an R-space and hence a strong $d$ -space. Suppose that $S$ is a subset of $P$ and $U\in \tau$ with $\bigcap _{s\in S}\mathord{\uparrow } s\subseteq U$ . We will show that there is a finite subset $S_0$ of $S$ such that $\bigcap _{s\in S_0}\mathord{\uparrow } s\subseteq U$ . If $S$ itself is finite, then we let $S_0=S$ . Now we assume that $S$ is (countably) infinite.

   Case 1: $|S\cap \textrm{max}(P)|\geq 2$ . Select any $s_1, s_2\in S\cap \textrm{max}(P)$ with $s_l\neq s_2$ . Then $\mathord{\uparrow } s_1\cap \mathord{\uparrow } s_2=\emptyset \subseteq U$ .

   Case 2: $|S\cap A|=1$ and $S\cap B=\emptyset$ . In this case, $S\cap \textrm{max}(P)=\{a_m\}$ for some $m\in \mathbb{N}$ and $S\cap \mathbb{N}$ is infinite. Select any $k\in S\cap \mathbb{N}$ with $m\lt k$ . Then $\mathord{\uparrow } k\cap \mathord{\uparrow } a_m=\emptyset \subseteq U$ .

   Case 3: $|S\cap B|=1$ and $S\cap A=\emptyset$ . Then $S\cap \textrm{max}(P)=\{\beta _l\}$ for some $l\in \mathbb{N}$ and $S\subseteq \mathord{\downarrow } \omega \cup \{\beta _l\}\cup \{a\}$ . Select any $s\in S\cap \mathord{\downarrow } \omega$ , Then $\mathord{\uparrow } s\cap \mathord{\uparrow } \beta _l=\bigcap _{s\in S\cap \mathord{\downarrow } \omega }\mathord{\uparrow } s\cap \mathord{\uparrow } \beta _l\cap \mathord{\uparrow } a=\bigcap _{s\in S}\mathord{\uparrow } s=\{\beta _l\}\subseteq U$ .

   Case 4: $S\cap \textrm{max}(P)=\emptyset$ . We have that $S\subseteq \mathord{\downarrow } \omega \cup \{a\}$ . If $a\in S$ , then $\bigcap _{s\in S}\mathord{\uparrow } s=B\subseteq U$ . So $A\setminus U$ is finite, and consequently, there is $k\in \mathbb{N}$ such that $\{a_k, a_{k+1}, \ldots \}\subseteq U$ . Select any $m\in S\cap \mathbb{N}$ with $m\gt k$ (note that $S\cap \mathbb{N}$ is infinite). Then $\mathord{\uparrow } m\cap \mathord{\uparrow } a=B\cup \{a_m, a_{m+1}, \ldots \}\subseteq B\cup \{a_k, a_{k+1}, \ldots \}\subseteq U$ . If $a\not \in S$ , then $\bigcap _{s\in S}\mathord{\uparrow } s=\mathord{\uparrow } \omega =B\cup \{\omega \}\subseteq U$ . By $\omega =\bigvee (S\cap \mathbb{N})$ and $U\in \tau \subseteq \sigma (P)$ , there is $n\in S\cap \mathbb{N}$ with $\mathord{\uparrow } n\subseteq U$ . Thus, by Theorem 35 $(P, \tau ))$ is an R-space.

8. (h) The product space $(P, \tau ))\times (P, \tau ))$ is not an R-space. It was proved in Li et al. (2023, Example 5.2) that $(P, \tau ))\times (P, \tau ))$ is not a strong $d$ -space. By Lemma 50, $(P, \tau ))\times (P, \tau ))$ is not an R-space.

By Example 51 and Li et al. (2023, Example 5.2), we pose the following question.

Question 52. Let $P, Q$ be dcpos for which $\Sigma P$ and $\Sigma Q$ are strong $d$ -spaces (resp., R-spaces). Must the product space $\Sigma P\times \Sigma Q$ be a strong $d$ -space (resp., an R-space)?

By Example 51 and MacLane (1997, pp. 92, Exercise 7) (or Nel and Wilson 1972, Remark 1.1), we get the following result.

Theorem 53. The category $\mathbf{Top}_r$ is not a reflective subcategory of $\mathbf{Top}_0$ .

For a dcpo $P$ , $(P, \upsilon (P))$ and $(P, \sigma (P))$ need not be strong $d$ -spaces, although they are always $d$ -spaces. Consider the Johnstone’s dcpo $\mathbb{J}=\mathbb{N}\times (\mathbb{N}\cup \{\infty \})$ with ordering defined by $(m,p)\leq (n,q)$ if $m=n$ and $p\leq q$ or if $p\leq n$ and $q=\infty$ . Then $(\mathbb{J}, \upsilon (\mathbb{J}))$ and the Johnstone space $\Sigma \,\!\mathbb{J}$ are $d$ -spaces. Clearly, $\bigcap _{n\in \mathbb{N}}\mathord{\uparrow } (1, n)\cap \mathord{\uparrow } (2,1)=\emptyset$ , but $\mathord{\uparrow } (1, n)\cap \mathord{\uparrow } (2,1)=\{(m, \omega ): n\leq m\}\neq \emptyset$ for all $n$ . Hence, $(\mathbb{J}, \upsilon (\mathbb{J}))$ and $\Sigma \,\!\mathbb{J}$ are not strong $d$ -spaces. Example 58 below shows that there is even an algebraic domain $P$ (hence $\Sigma P$ is sober) such that $\Sigma P$ is not a strong $d$ -space.

The following example shows that a locally compact and second-countable strong $d$ -space may not be a well-filtered space in general (and hence not sober). So a locally compact strong $d$ -space may not be sober (in contrast to Theorem29) and a second-countable strong $d$ -space need not be sober (in contrast to Xu et al. 2020a, Theorem 4.2).

Example 54. Let $X$ be a countably infinite set and $X_{cof}$ the space equipped with the co-finite topology (the empty set and the complements of finite subsets of $X$ are open). Then

1. (a) $\mathscr{O}(X_{cof})$ is countable, whence $X_{cof}$ is second-countable.

2. (b) $\mathscr{C}(X_{cof})=\{\emptyset, X\}\bigcup X^{(\lt \omega )}$ , $X_{cof}$ is $T_1$ and hence a strong $d$ -space.

3. (c) $\mathord{\mathsf{K}} (X_{cof})=2^X\setminus \{\emptyset \}$ . So $X_{cof}$ is locally compact.

4. (d) $X_{cof}$ is not well-filtered and hence non-sober. Let $\mathscr{K}=\{X\setminus F : F\in X^{(\lt \omega )}\}$ . Then $\mathscr{K}$ is a filtered family of compact saturated sets of $X_{cof}$ and $\bigcap \mathscr{K}=\bigcap \limits _{F\in X^{(\lt \omega )}}(X\setminus F)=X\setminus \bigcup X^{(\lt \omega )}=\emptyset$ , but $X\setminus F\neq \emptyset$ for any $F\in X^{(\lt \omega )}$ . So $X_{cof}$ is not well-filtered.

The following result follows directly from Proposition 11(4).

Proposition 55. Let $P$ be a Noetherian dcpo and $\tau$ an order-compatible topology on $P$ (i.e., $\upsilon (P) \subseteq \tau \subseteq \alpha (P)$ ). Then $(P, \tau )$ is a strong $d$ -space.

In the following example, we give a Noetherian dcpo $P$ such that $\Sigma P$ is not an R-space, though it is both a strong $d$ -space and a sober space. It also shows that there exists a Noetherian dcpo $P$ such that $(P, \tau )$ is not an R-space for any order-compatible topology on $P$ (in contrast to Proposition 55).

Example 56. Let $P=\{a_1, a_2, \ldots, a_n, \ldots \}\cup \{b_1, b_2, \ldots, b_n, \ldots \}$ with the order generated by $a_n\lt b_m$ iff $n\leq m$ in $\mathbb{N}$ and $\tau$ an order-compatible topology on $P$ . Then $P$ is a Noetherian dcpo. Hence by Proposition 55, $(P, \sigma (P))$ is both a strong $d$ -space and a sober space. Clearly, $\bigcap _{n\in \mathbb N}\mathord{\uparrow } a_n=\bigcap _{n\in \mathbb N}(\{a_n\}\cup \{b_m : n\leq m\})=\emptyset$ , but for any finite subset $\{n_1, n_2, \ldots, n_m\}$ of $\mathbb N$ , $\bigcap \limits _{j=1}^{m}\mathord{\uparrow } a_{n_j}\supseteq \{b_l : \mbox{max}\{n_1, n_2, \ldots, n_m\}\leq l\}\neq \emptyset$ . So $(P, \tau )$ is not an R-space. In particular, neither $(P, \upsilon (P))$ nor $\Sigma P$ is an R-space.

Proposition 57. Let $X$ be a well-filtered space and $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is compact for all $x, y\in X$ . Then $X$ is a strong $d$ -space.

Proof. Let $D\in \mathscr{D}(X)$ , $x\in X$ and $U\in \mathscr{O}(X)$ such that $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ holds. If there is $d_0\in D$ such that $\mathord{\uparrow } d_0\cap \mathord{\uparrow } x=\emptyset$ , then $\mathord{\uparrow } d_0\cap \mathord{\uparrow } x\subseteq U$ . Now assume that $\mathord{\uparrow } d\cap \mathord{\uparrow } x\neq \emptyset$ for all $d\in D$ . Then by assumption $\{\mathord{\uparrow } d\cap \mathord{\uparrow } x : d\in D\}$ is a filtered family of compact saturated subsets of $X$ and $\bigcap _{d\in D}(\mathord{\uparrow } d\cap \mathord{\uparrow } x)= \bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ . By the well-filteredness of $X$ , there is $d\in D$ such that $\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ . So $X$ is a strong $d$ -space.

The following example shows that even for an algebraic domain $P$ , if the condition that $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is compact for all $x, y\in P$ is not satisfied, $\Sigma P$ may not be a strong $d$ -space. It also shows that a sober space need not be a strong $d$ -space, and hence, well-filtered spaces and $d$ -spaces are generally not strong $d$ -spaces.

Example 58. Let $C=\{a_1, a_2, \ldots, a_n, \ldots \}\cup \{\omega _0\}$ and $P=C\cup \{b\}\cup \{\omega _1, \ldots, \omega _n, \ldots \}$ . Define an order on $P$ as follows (see Fig. 3 ):

1. (i) $a_1\lt a_2\lt \ldots \lt a_n\lt a_{n+1}\lt \ldots$ ;

2. (ii) $a_n\lt \omega _0$ for all $n\in \mathbb{N}$ ;

3. (iii) $b\lt \omega _n$ and $a_m\lt \omega _n$ for all $n, m\in \mathbb{N}$ with $m\leq n$ .

Figure 3. The poset $P$ in Example 58.

1. (a) $D\in \mathscr{D}(P)$ iff $D\subseteq C$ is an infinite chain or $D$ has a largest element. So $P$ is a dcpo. Clearly, $\textrm{max}(P)=\{\omega _0, \omega _1, \omega _2, \ldots, \omega _n, \ldots \}$ . If $D\subseteq C$ is an infinite chain or $D$ has a largest element, then $D\in \mathscr{D}(P)$ . Conversely, suppose $D$ is a directed subset of $P$ and $D$ has no largest element. Then $D$ is countably infinite and $|D\cap \textrm{max}(P)|\lt 2$ . If there exits $\omega _m\in D$ for some $m\in \mathbb{N}$ , then for any $d\in D$ , by the directedness of $D$ , there is $d^{\prime }\in D$ such that $d\leq d^{\prime }$ and $\omega _m\leq d^{\prime }$ . Then $d\leq d^{\prime }=\omega _m$ . So $\omega _m$ is the largest element of $D$ , a contradiction. Hence, $D\cap \textrm{max}(P)=\emptyset$ , that is, $D\subseteq C\cup \{b\}$ . Since for any $n\in \mathbb{N}$ , $a_n$ and $b$ have no upper bound in $D$ , we have $b\not \in D$ , and hence, $D\subseteq C$ is an infinite chain.

2. (b) $P$ is an algebraic domain. By (a), $x\ll x$ for all $x\in P\setminus \{\omega _0\}$ . Hence, $P$ is an algebraic domain.

3. (c) $\Sigma P$ is sober and not coherent. By (b) and Proposition III-3.7 of Gierz et al. (2003) or Proposition 4.4 of Gierz et al. (1983), $\Sigma P$ is sober. Clearly, $\mathord{\uparrow } a_1, \mathord{\uparrow } b\in \mathord{\mathsf{K}} (\Sigma \,)$ , but $\mathord{\uparrow } a_1\cap \mathord{\uparrow } b=\{\omega _1, \omega _2, \ldots, \omega _n, \ldots \}$ is not Scott-compact (note $\{\omega _n\}\in \sigma (P)$ for all $n\in \mathbb{N}$ ) and hence $\Sigma P$ is not coherent.

4. (d) $\Sigma P$ is not a strong $d$ -space. Since $\bigcap _{n\in \mathbb{N}}\mathord{\uparrow } a_n\cap \mathord{\uparrow } b=\emptyset$ but $\mathord{\uparrow } a_m\cap \mathord{\uparrow } b=\{\omega _m, \omega _{m+1}, \ldots \}\neq \emptyset$ for all $m\in \mathbb N$ , $P$ with any order-compatible topology is not a strong $d$ -space. In particular, $(P, \upsilon (P))$ and $\Sigma P$ are not strong $d$ -spaces.

Remark 59. Let $\hat{P}$ be the poset obtained from $P$ by adding an order relation $b\lt \omega _0$ (see Fig. 4 ). Then $\Sigma \hat{P}$ is a strong $d$ -space. We will give a short proof. Suppose $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ , where $D\in \mathscr{D}(\hat{P})$ , $x\in P$ and $U\in \mathcal \sigma (\hat{P})$ . If $D$ has a largest element $s$ , then $\mathord{\uparrow } s\cap \mathord{\uparrow } x=\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq U$ . Now assume that $D$ has no largest element. Then $D\subseteq C=\{a_1, a_2, \ldots, a_n, \ldots \}$ is an infinite chain and $\omega _0=\bigvee D$ . Hence, $\bigcap _{d\in D}\mathord{\uparrow } d=\{\omega _0\}$ . If $x=\omega _0$ , then $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x=\{\omega _0\}\subseteq U$ and hence $\mathord{\uparrow } d\cap \mathord{\uparrow } x=\{\omega _0\}\subseteq U$ for all $d\in D$ . If $x=\omega _m$ for some $m\in \mathbb{N}\setminus \{0\}$ , then $x\not \in \{\omega _0\}=\bigcap _{d\in D}\mathord{\uparrow } d$ and hence there is a $d\in D$ such that $\mathord{\uparrow } d\cap \mathord{\uparrow } x=\emptyset \subseteq U$ . If $x\in C\cup \{b\}$ , then $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x=\{\omega _0\}\subseteq U$ . As $\omega _0=\bigvee D$ , there is $d\in D$ with $\mathord{\uparrow } d\subseteq U$ , whence $\mathord{\uparrow } d\cap \mathord{\uparrow } x\subseteq \mathord{\uparrow } d\subseteq U$ . Thus, $\Sigma \hat{P}$ is a strong $d$ -space.

Figure 4. The poset $\hat{P}$ in Remark 59.

Now we give some characterizations of strong $d$ -spaces. In the following, when a $T_0$ -space is also considered as a poset, the order refers to the specialization order.

Let $X$ be a $T_0$ -space and $\mathscr{G}$ a family of subsets of $X$ closed under arbitrary intersections such that $\mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}\subseteq \mathscr{G}\subseteq \mathbf{up}(X)$ . Endow $\mathscr{G}$ with the reverse inclusion order $\sqsubseteq$ , that is, for $G_1, G_2\in \mathscr{G}$ , $G_1\sqsubseteq G_2$ iff $G_2\subseteq G_1$ . Denote $\mathscr{G}$ equipped with the Scott topology for this order by $\Sigma \mathscr{G}$ . For any $x\in X$ , it is straightforward to verify that the mapping $y\mapsto \mathord{\uparrow } y\cap \mathord{\uparrow } x : X \rightarrow \mathscr{G}$ is Scott continuous. Furthermore, the mapping $m_{\sigma } : X\times X\rightarrow \mathscr{G}, (x,y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is Scott continuous. Indeed, if $\{(x_{d},y_{d}):d\in D\}\in \mathscr{D} (X\times X)$ for which $\bigvee _{d\in D}(x_d, y_d)$ exists in $X\times X$ , then $\{x_{d}:d\in D\}\in \mathscr{D}(X)$ , $\{y_{d}:d\in D\}\in \mathscr{D}(X)$ , and $\bigvee _{d\in D}x_d$ and $\bigvee _{d\in D} y_d$ exist in $X$ . Clearly, $m_{\sigma }(\bigvee _{d\in D}(x_{d},y_{d}))=m_{\sigma }((\bigvee _{d\in D}x_{d},\bigvee _{d\in D}y_{d}))=(\mathord{\uparrow } \bigvee _{d\in D}x_{d})\cap (\mathord{\uparrow }\bigvee _{d\in D}y_{d})=(\bigcap _{d\in D}\mathord{\uparrow } x_{d})\cap (\bigcap _{d\in D}\mathord{\uparrow } y_{d})=\bigcap _{d\in D}(\mathord{\uparrow } x_{d}\cap \mathord{\uparrow } y_{d})=\bigcap _{d\in D}m_{\sigma }(x_{d},y_{d})=\bigvee _{\mathscr{G}}\{m_{\sigma }(x_{d},y_{d}) : d\in D\}$ . By Lemma 4, $m_{\sigma }:\Sigma (X\times X) \rightarrow \Sigma \mathscr{G}$ is continuous.

Proposition 60. Let $X$ be a $T_0$ -space and $\mathscr{G}$ a family of subsets of $X$ closed under arbitrary intersections such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . Then the following four conditions are equivalent:

1. (1) For any $A\in \mathscr{C}(X)$ and $x\in X$ , $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

2. (2) For any $A\in \mathscr{C}(X)$ and $K\in \mathord{\mathsf{K}} (\Sigma \,\!\!X)$ , $\mathord{\downarrow } (K\cap A)\in \mathscr{C}(\Sigma X)$ .

3. (3) For all $x\in X$ , the mapping $m_x : \Sigma X \rightarrow P_S(\mathscr{G}), y\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

4. (4) The mapping $m : \Sigma (X\times X) \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

Proof. (1) $\Leftrightarrow$ (2): It is proved in Xu and Zhao (2020) (see the proof of Xu and Zhao 2020, Lemma 3.15) for $d$ -spaces and the proof is valid for general $T_0$ -spaces.

(1) $\Rightarrow$ (3): For $U\in \mathscr{O}(X)$ , we show that $m_x^{-1}(\Box _{\mathscr{G}}U)=\{y\in X : \mathord{\uparrow } x\cap \mathord{\uparrow } y\subseteq U\}\in \sigma (X)$ . Clearly, $m_x^{-1}(\Box _{\mathscr{G}}U)$ is an upper set of $P$ . Suppose that $D\in \mathscr{D}(P)$ with $\bigvee D$ existing and $\bigvee D\in m_x^{-1}(\Box _{\mathscr{G}}U)$ . Then $\mathord{\uparrow } x\cap \mathord{\uparrow } \bigvee D \subseteq U$ . Let $A=X\setminus U$ . Then $A\in \mathscr{C}(X)$ and $(\mathord{\uparrow } \bigvee D) \cap \mathord{\uparrow } x\cap A=\emptyset$ . Hence, $\bigvee D\not \in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ by (1). It follows that $D\not \subseteq \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ , and consequently, there is $d\in D$ such that $d\not \in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . So $\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A=\emptyset$ , that is, $d\in m_x^{-1}(\Box _{\mathscr{G}}U)$ . Thus, $m_x^{-1}(\Box _{\mathscr{G}}U)\in \sigma (P)$ . Therefore, $m_x : \Sigma P \rightarrow P_S(\mathscr{G})$ is continuous.

(3) $\Rightarrow$ (4): Let $U\in \sigma (X)$ . We show that $m^{-1}(\Box _{\mathscr{G}}U)=\{(x, y)\in X\times X : \mathord{\uparrow } x\cap \mathord{\uparrow } y\subseteq U\}\in \sigma (X\times X)$ . Clearly, $m^{-1}(\Box _{\mathscr{G}}U)$ is an upper set of $X\times X$ . Suppose that $D\in \mathscr{D}(X\times X)$ such that $\bigvee D$ existing and $\bigvee D\in m^{-1}(\Box _{\mathscr{G}}U)$ . Let $p_i : X\times X \rightarrow X$ be the $i$ th projection ( $i=1, 2$ ). Then $D_i=p_i(D)$ is a directed subset of $X$ ( $i=1, 2$ ) and $\bigvee D=(\bigvee D_1, \bigvee D_2)$ . Hence, $m_{\bigvee D_2}(\bigvee D_1)=(\mathord{\uparrow } \bigvee D_1)\cap (\mathord{\uparrow } \bigvee D_2)=m(\bigvee D)\in \Box _{\mathscr{G}}U$ . By (3), there is $d_1\in D$ such that $m_{p_1(d_1)}(\bigvee D_2)=(\mathord{\uparrow } p_1(d_1))\cap (\mathord{\uparrow } \bigvee D_2)\in \Box _{\mathscr{G}}U$ . By (3) again, there is $d_2\in D$ such that $(\mathord{\uparrow } p_1(d_1))\cap (\mathord{\uparrow } p_2(d_2))\in \Box _{\mathscr{G}}U$ . By the directedness of $D$ , there is $d_3\in D$ with $d_1\leq d_3$ and $d_2\leq d_3$ . Then $m(d_3)=(\mathord{\uparrow } p_1(d_3))\cap (\mathord{\uparrow } p_2(d_3))\subseteq (\mathord{\uparrow } p_1(d_1))\cap (\mathord{\uparrow } p_2(d_2))\in \Box _{\mathscr{G}}U$ and hence $d_3\in m^{-1}(\Box _{\mathscr{G}}U)$ . Thus, $m : \Sigma (X\times X) \rightarrow P_S(\mathscr{G})$ is continuous.

(4) $\Rightarrow$ (1): For $A\in \mathscr{C}(X)$ and $x\in X$ , we show that $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ . Suppose that $D$ is a directed subset of $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ with $\bigvee D$ existing. If $\bigvee D\not \in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . Then $U=X\setminus A\in \mathscr{O}(X)$ and $(\mathord{\uparrow } \bigvee D)\cap \mathord{\uparrow } x\subseteq U$ . Let $D_x=\{(d, x) : d\in D\}$ . Then $D_x\in \mathscr{D}(X\times X)$ and $m(\bigvee D_x)=m((\bigvee D, x))=(\mathord{\uparrow } \bigvee D)\cap \mathord{\uparrow } x \subseteq U$ . Hence, $\bigvee D_x\in m^{-1}(\Box _{\mathscr{G}}U)\in \sigma (X\times X)$ by (4). It follows that $(d, x)\in m^{-1}(\Box _{\mathscr{G}}U)$ for some $d\in D$ , that is, $d\not \in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ , a contradiction, proving that $\bigvee D\not \in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . So $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

Based on Proposition 60, we obtain the following characterizations of strong $d$ -spaces.

Theorem 61. Let $X$ be a $T_0$ -space and $\mathscr{G}$ a family of subsets of $X$ closed under intersection such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in X\}$ . Then the following conditions are equivalent:

1. (1) $X$ is a strong $d$ -space.

2. (2) For any $D\in \mathscr{D}(X)$ , $\mathord{\uparrow } F\in \mathbf{Fin} X$ and $U\in \mathscr{O}(X)$ , $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } F\subseteq U$ implies $\mathord{\uparrow } d\cap \mathord{\uparrow } F\subseteq U$ for some $d\in D$ .

3. (3) $X$ is a $d$ -space, and for any $A\in \mathscr{C}(X)$ and $x\in X$ , $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

4. (4) $X$ is a dcpo, and for any $A\in \mathscr{C}(X)$ and $x\in X$ , $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

5. (5) $X$ is a dcpo, and for any $A\in \mathscr{C}(X)$ and $K\in \mathord{\mathsf{K}} (\Sigma \,\!\!X)$ , $\mathord{\downarrow } (K\cap A)\in \mathscr{C}(\Sigma X)$ .

6. (6) $X$ is a dcpo, and for all $x\in X$ , the mapping $m_x : \Sigma X \rightarrow P_S(\mathscr{G}), y\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

7. (7) $X$ is a dcpo, and the mapping $m : \Sigma (X\times X) \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

Proof. (1) $\Leftrightarrow$ (2): Obviously, (2) $\Rightarrow$ (1). Conversely, suppose that $X$ is a strong $d$ -space, $D\in \mathscr{D}(X)$ , $\mathord{\uparrow } F\in \mathbf{Fin} X$ and $U\in \mathscr{O}(X)$ such that $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } F\subseteq U$ . Then for each $u\in F$ , $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } u\subseteq U$ , and hence $\mathord{\uparrow } d_u\cap \mathord{\uparrow } u\subseteq U$ for some $d_u\in D$ . Since $F$ is finite and $D$ is a direct subset of $X$ , there is a $d_0\in D$ such that $\mathord{\uparrow } d_0\subseteq \bigcap _{u\in F}\mathord{\uparrow } d_u$ . It follows that $\mathord{\uparrow } d_0\cap \mathord{\uparrow } F=\bigcup _{u\in F}\mathord{\uparrow } d_0\cap \mathord{\uparrow } u\subseteq \bigcup _{u\in F}\mathord{\uparrow } d_u\cap \mathord{\uparrow } u\subseteq U$ .

(1) $\Rightarrow$ (3): Suppose that $X$ is a strong $d$ -space. Then by Proposition 20, $X$ is a $d$ -space and hence $X$ is a dcpo. For $A\in \mathscr{C}(X)$ and $x\in X$ , we show that $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ . Let $D\in \mathscr{D}(X)$ with $D\subseteq \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . Then $\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A\neq \emptyset$ for all $d\in D$ . As $X$ is a strong $d$ -space, $\bigcap _{d\in D}(\mathord{\uparrow } d\cap \mathord{\uparrow } x)\cap A\neq \emptyset$ or, equivalently, $\uparrow \bigvee D \cap \mathord{\uparrow } x\cap A\neq \emptyset$ . Hence, $\bigvee D\in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . So $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

(3) $\Rightarrow$ (4): Trivial.

(4) $\Leftrightarrow$ (5) $\Leftrightarrow$ (6) $\Leftrightarrow$ (7): By Proposition 60.

(4) $\Rightarrow$ (1): Let $D\in \mathscr{D}(X)$ , $x\in X$ and $A\in \mathscr{C}(X)$ . If $\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A\neq \emptyset$ for all $d\in D$ , then $D\subseteq \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . By (4), $\bigvee D\in \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ , namely, $\bigcap _{d\in D}\mathord{\uparrow } d \cap \mathord{\downarrow } (\mathord{\uparrow } x\cap A)$ . Hence, $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } x\cap A\neq \emptyset$ . Thus, $X$ is a strong $d$ -space.

Remark 62. Let $X$ be a $T_0$ -space and $\mathscr{G}$ a family of subsets of $X$ closed under intersection such that $\mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in X\}\subseteq \mathscr{G}\subseteq \mathbf{up}(P)$ . It is easy to verify that the specialization order of $P_S(\mathscr{G})$ is the Smyth order (i.e.,, $\leq _{P_S(\mathscr{G})}=\sqsubseteq$ ). When $\mathscr{G}$ is equipped with the Smyth order, the mappings $m_x : \Sigma X \rightarrow P_S(\mathscr{G})$ and $m : \Sigma (X\times X) \rightarrow P_S(\mathscr{G})$ are defined by $m_x(y)=\mathord{\uparrow } x\bigvee _{P_S(\mathscr{G})} \mathord{\uparrow } y=\mathord{\uparrow } x\bigvee _{\mathscr{G}} \mathord{\uparrow } y$ and $m((u, v))=\mathord{\uparrow } u\bigvee _{P_S(\mathscr{G})} \mathord{\uparrow } v=\mathord{\uparrow } u\bigvee _{\mathscr{G}} \mathord{\uparrow } v$ . The preceding theorem indicates that the notion of a strong $d$ -space can be seen as a variant of join continuity.

Corollary 63. Let $P$ be a poset and $\mathscr{G}$ a family of subsets of $P$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . Then the following conditions are equivalent:

1. (1) $\Sigma P$ is a strong $d$ -space.

2. (2) For any $D\in \mathscr{D}(P)$ , $\mathord{\uparrow } F\in \mathbf{Fin} P$ and $U\in \sigma (P)$ , $\bigcap _{d\in D}\mathord{\uparrow } d\cap \mathord{\uparrow } F\subseteq U$ implies $\mathord{\uparrow } d\cap \mathord{\uparrow } F\subseteq U$ for some $d\in D$ .

3. (3) $P$ is a dcpo, and for any $A\in \mathscr{C}(\Sigma P)$ and $x\in P$ , $\mathord{\downarrow } (\mathord{\uparrow } x\cap A)\in \mathscr{C}(\Sigma X)$ .

4. (4) $P$ is a dcpo, and for any $A\in \mathscr{C}(\Sigma P)$ and $K\in \mathord{\mathsf{K}} (\Sigma \,\!\!P)$ , $\mathord{\downarrow } (K\cap A)\in \mathscr{C}(\Sigma P)$ .

5. (5) $X$ is a dcpo, and for all $x\in X$ , the mapping $m_x : \Sigma P \rightarrow P_S(\mathscr{G}), y\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

6. (6) $P$ is a dcpo, and the mapping $m : \Sigma (P\times P) \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

For $\mathscr{G}=\mathbf{up}(P)$ , the equivalences of conditions (1), (3), (4), and (5) in Corollary 63 were also given in Miao et al. (2021, Lemma 3.2 and Proposition 3.3).

The following result follows directly from Proposition 26 and Corollary 63(4).

Corollary 64. For a dcpo $P$ , if $\Sigma P$ is a strong $d$ -space, then it is well-filtered.

Remark 65. Note that Corollary 64, together with Lemma 50(3), is an improvement on Theorem  43 .

Corollary 66. Let $P$ be a dcpo. If $\Sigma P$ is core-compact (especially, locally compact) and a strong $d$ -space, then $\Sigma P$ is sober.

Proof. By Theorem29 and Corollary 64.

Corollary 67. (Miao et al. 2021 , Corollary 3.6) Let $P$ be a Scott-compact poset such that $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is Scott-compact for all $x, y\in P$ (in particular, $\Sigma P$ is coherent). Then the following three conditions are equivalent:

1. (1) $\Sigma P$ is an R-space.

2. (2) $\Sigma P$ is a strong $d$ -space.

3. (3) $\Sigma P$ is well-filtered.

Proof. By Lemma 50(3), (1) implies (2), and (2) implies (3) by Corollary 64. The implication (3) implies (1) follows from Lemma 25, Proposition 33, and the equivalence of property R and $\Omega ^{\star }$ -compactness (Theorem35).

By Theorem44 and Corollary 67, we get the following corollary.

Corollary 68. For a dcpo $P$ , the following two conditions are equivalent:

1. (1) $(P,\lambda (P))$ is compact.

2. (2) $\Sigma P$ is a compact strong $d$ -space and $\mathord{\uparrow } x\cap \mathord{\uparrow } y$ is Scott-compact for all $x, y\in P$ .

In Xu et al. (2020a), it was proved that every first-countable well-filtered space is sober (see Xu et al. 2020a, Theorem 4.2). By this result and Corollary 64, we deduce the following result.

Proposition 69. Let $P$ be a dcpo for which $\Sigma P$ is first-countable and a strong $d$ -space (especially, an R-space). Then $\Sigma P$ is sober.

For a $T_0$ -space $X$ and $\mathscr{G}$ a family of subsets of $X$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ , there is naturally another mapping from $X\times X$ to $\mathscr{G}$ , more precisely, the mapping $m^{\star } : X\times X \rightarrow P_S(\mathscr{G})$ defined by $m^{\star }((x, y))=\mathord{\uparrow } x\cap \mathord{\uparrow } y$ for all $(x, y)\in X\times X$ . In this way, for $x\in X$ , one can define a mapping $m^{\star }_x : X \rightarrow P_S(\mathscr{G})$ by $m^{\star }_x(y)=\mathord{\uparrow } x\cap \mathord{\uparrow } y$ for all $y\in X$ . It is easy to verify that the continuity of $m^{\star }$ implies the continuity of $m^{\star }_x$ for all $x\in X$ . The following example shows that the converse fails in general (comparing it with the equivalence of conditions (3) and (4) in Proposition 60). It also shows that even for a strong $d$ -space $X$ , the mapping $m^{\star } : X\times X \rightarrow P_S(\mathscr{G})$ may not be continuous.

Example 70. Let $X$ be a countably infinite set and $X_{cof}$ the space equipped with the co-finite topology (see Example 54) and $\mathscr{G}$ a family of subsets of $X$ such that $\mathscr{G}\supseteq \mathcal \{\{x\} : x\in X\}$ . Then

1. (a) $X_{cof}$ is a locally compact $T_1$ -space.

2. (b) $X_{cof}$ is a strong $d$ -space but not well-filtered.

3. (c) For each $x\in X$ , $m^{\star }_x : X_{cof} \rightarrow P_S(\mathscr{G}), y\mapsto \{x\}\cap \{y\}$ , is continuous. For $y\in X$ , we have

   \begin{equation*}m^{\star }_x(y)= \begin {cases} \emptyset, & y\neq x\\ \{x\},& y=x. \end {cases}\end{equation*}
   Therefore, for any $U\in \mathscr{O}(X_{cof})$ ,
   \begin{equation*}(m^{\star }_x)^{-1}(U)= \begin {cases} X,& x\in U\\ X\setminus \{x\},& x\not \in U. \end {cases}\end{equation*}
   So $m^{\star }_x : X_{cof} \rightarrow P_S(\mathscr{G})$ is continuous.

4. (d) $m^{\star } : X_{cof}\times X_{cof} \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \{x\}\cap \{y\}$ , is not continuous. Assume, on the contrary, that $m^{\star }$ is continuous. Then $(m^{\star })^{-1}(\Box _{\mathscr{G}}\emptyset )=\{(x, y)\in X\times X : \{x\}\cap \{y\}=\emptyset \}=X\times X\setminus \{(x, x) : x\in X\}\in \mathscr{O}(X_{cof}\times X_{cof})$ . Hence, for two different point $s, t\in X$ (i.e., $s\neq t$ ), there are $F, G\in X^{(\lt \omega )}$ such that $(s, t)\in (X\setminus F)\times (X\setminus G)\subseteq (m^{\star })^{-1}(\Box _{\mathscr{G}}\emptyset )$ . Select a point $u\in X\setminus (F\cup G)$ . Then $(u, u)\in (X\setminus F)\times (X\setminus G)\subseteq X\times X\setminus \{(x, x) : x\in X\}$ , a contradiction. Thus, $m^{\star } : X_{cof}\times X_{cof} \rightarrow P_S(\mathscr{G})$ is not continuous.

As an immediate corollary of Theorem61 (or Corollary 63), we get the following.

Proposition 71. Let $P$ be a poset for which $\Sigma P$ is a strong $d$ -space and $\mathscr{G}$ a family of subsets of $P$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . If $\Sigma (P\times P)=\Sigma P\times \Sigma P$ , then the mapping $m^{\star } : \Sigma P\times \Sigma P \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous.

From Theorem17 and Proposition 71, we deduce the following.

Corollary 72. Let $P$ be a poset for which $\Sigma P$ is a strong $d$ -space and $\mathscr{G}$ a family of subsets of $P$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . If $\Sigma P$ is core-compact (especially, locally compact), then the mapping $m^{\star } : \Sigma P\times \Sigma P \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ is continuous.

Finally, we give some conditions on a $d$ -space $X$ under which $X$ is sober. In particular, we show that for a dcpo $P$ , if $\Sigma P$ is a strong $d$ -space and $\Sigma (P\times P)=\Sigma P\times \Sigma P$ , then $\Sigma P$ is sober.

Proposition 73. Let $X$ be a $d$ -space and $\mathscr{G}$ a family of subsets of $X$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . If the mapping $m^{\star } : X\times X \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ is continuous, then $X$ is sober.

Proof. Since $X$ is a $d$ -space, $X$ (with the specialization order) is a dcpo and $\mathscr{C}(X)\subseteq \mathscr{C}(\Sigma X)$ . Suppose that $A\in{\mathsf{Irr}}_c(X)$ . We show that $A$ is directed. Assume, on the contrary, that $A$ is not directed. Then there exist $b, c\in A$ such that $\mathord{\uparrow } b\cap \mathord{\uparrow } c\cap A=\emptyset$ or, equivalently, $(b, c)\in (m^{\star })^{-1}(\Box _{\mathscr{G}}(X\setminus A))$ . As $m^{\star } : X\times X \rightarrow P_S(\mathscr{G})$ is continuous, $(m^{\star })^{-1}(\Box _{\mathscr{G}}(X\setminus A))\in \mathscr{O}(X\times X)$ . Hence, there exist $V, W\in \mathscr{O}(X)$ such that $(b,c)\in V\times W\subseteq (m^{\star })^{-1}(\Box _{\mathscr{G}}(X\setminus A))$ . As $A\in{\mathsf{Irr}}_c(X$ , $A\cap V\neq \emptyset$ and $A\cap W\neq \emptyset$ , we have that $A\cap V\cap W\neq \emptyset$ . Select a $z\in A\cap V\cap W$ . Then $m^{\star }(z,z)=\mathord{\uparrow } z\cap \mathord{\uparrow } z=\mathord{\uparrow } z\in (m^{\star })^{-1}(\Box _{\mathscr{G}}(X\setminus A))$ , that is $\mathord{\uparrow } z\subseteq X\setminus A$ , a contradiction. So $A$ is directed and hence $\bigvee A\in A$ , and consequently, $A=\mathord{\downarrow } \bigvee A={\textrm{cl}}_{X}\{\bigvee A\}$ . Thus, $X$ is sober.

Corollary 74. Let $P$ be a dcpo and $\mathscr{G}$ a family of subsets of $X$ such that $\mathscr{G}\supseteq \mathscr{S}^u_2=\{\mathord{\uparrow } x\cap \mathord{\uparrow } y : x, y\in P\}$ . If the mapping $m^{\star } : \Sigma P\times \Sigma P \rightarrow P_S(\mathscr{G}), (x, y)\mapsto \mathord{\uparrow } x\cap \mathord{\uparrow } y$ , is continuous, then $\Sigma P$ is sober.

From Theorem61 and Proposition 73, we deduce the following.

Proposition 75. If $X$ is a strong $d$ -space and $X\times X=\Sigma (X\times X)$ , then $X$ is sober.

As an immediate corollary of Proposition 75, we get the following important result.

Theorem 76. If $P$ is a dcpo such that $\Sigma P$ is a strong $d$ -space and $\Sigma (P\times P)=\Sigma P\times \Sigma P$ , then $\Sigma P$ is sober.

Corollary 77. Let $P$ be a dcpo for which $\Sigma (P\times P)=\Sigma P\times \Sigma P$ . If $P$ satisfies one of the following conditions:

1. (1) $P$ is a complete lattice.

2. (2) $(P, \lambda (P))$ is compact.

3. (3) $(P, \lambda (P))$ is upper-semicompact.

4. (4) $\Sigma P$ is well-filtered and coherent.

5. (5) $\Sigma P$ is an R-space.

Then $\Sigma P$ is sober.

Proof. By Lemma 6, Propositions 42 and 33(2), we have that (1) $\Rightarrow$ (2) $\Rightarrow$ (3) $\Rightarrow$ (5) and (4) $\Rightarrow$ (5). By Lemma 50(3), (5) implies that $\Sigma P$ is a strong $d$ -space. Therefore, we get Corollary 77 by Theorem76.

Remark 78. If $P$ is a dcpo such that $\Sigma P$ is a first-countable strong $d$ -space, then by Theorem 4.2 of Xu et al. (2020a) and Corollary 64 we also get the sobriety of $\Sigma P$ .