Contents
Editorial Preface
Preface for the special issue on domains
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 105-106
-
- Article
-
- You have access
- Export citation
Paper
Domain representations of spaces of compact subsets
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 107-126
-
- Article
- Export citation
Selection functions, bar recursion and backward induction
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 127-168
-
- Article
- Export citation
De Groot duality and models of choice: angels, demons and nature†
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 169-237
-
- Article
- Export citation
Some reasons for generalising domain theory
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 239-265
-
- Article
- Export citation
The limit–colimit coincidence theorem for
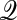 -categories
-categories
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 267-284
-
- Article
- Export citation
On universal algebra over nominal sets
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 285-318
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MSC volume 20 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
MSC volume 20 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. b1-b4
-
- Article
-
- You have access
- Export citation

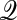 -categories
-categories