Contents
Foreword
Foreword: special issue in memory of Nadia Busi
-
- Published online by Cambridge University Press:
- 04 December 2009, pp. 1061-1063
-
- Article
-
- You have access
- Export citation
Paper
From parametric polymorphism to models of polymorphic FPC
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 639-686
-
- Article
- Export citation
Introduction
Editors' note: bibliometrics and the curators of orthodoxy
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 1-4
-
- Article
-
- You have access
- Export citation
Paper
Social processes, program verification and all that
-
- Published online by Cambridge University Press:
- 07 September 2009, pp. 877-896
-
- Article
- Export citation
On traced monoidal closed categories
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 217-244
-
- Article
- Export citation
Exploring the relation between Intuitionistic BI and Boolean BI: an unexpected embedding
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 435-500
-
- Article
- Export citation
Effective λ-models versus recursively enumerable λ-theories
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. 897-942
-
- Article
- Export citation
Predicate transformers for extended probability and non-determinism
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 501-539
-
- Article
- Export citation
Structural non-interference in elementary and trace nets
-
- Published online by Cambridge University Press:
- 04 December 2009, pp. 1065-1090
-
- Article
- Export citation
Two-dimensional models of type theory
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 687-736
-
- Article
- Export citation
Editorial Preface
Preface to Special Issue: Theory and Applications of Models of Computation (TAMC)
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 5-7
-
- Article
-
- You have access
- Export citation
Paper
Correctness of high-level transformation systems relative to nested conditions†
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 245-296
-
- Article
- Export citation
Automata theory based on unsharp quantum logic†
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 737-756
-
- Article
- Export citation
Process discovery and Petri nets†
-
- Published online by Cambridge University Press:
- 04 December 2009, pp. 1091-1124
-
- Article
- Export citation
A quantitative computational model for complete partial metric spaces via formal balls†
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 541-563
-
- Article
- Export citation
On a measurement-free quantum lambda calculus with classical control
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 297-335
-
- Article
- Export citation
Phase transition of multivariate polynomial systems
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 9-23
-
- Article
- Export citation
The sequential topology on
 is not regular
is not regular
-
- Published online by Cambridge University Press:
- 08 September 2009, pp. 943-957
-
- Article
- Export citation
On the expressive power of process interruption and compensation
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 565-599
-
- Article
- Export citation
Algebra and logic for resource-based systems modelling
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. 959-1027
-
- Article
- Export citation

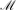
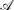
 is not regular
is not regular