Contents
Paper
De Groot duality and models of choice: angels, demons and nature†
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 169-237
-
- Article
- Export citation
Bounded minimalisation and bounded counting in argument-bounded idc's
-
- Published online by Cambridge University Press:
- 27 October 2010, pp. 753-779
-
- Article
- Export citation
Limits to measurement in experiments governed by algorithms†
-
- Published online by Cambridge University Press:
- 08 November 2010, pp. 1019-1050
-
- Article
- Export citation
Modal and mixed specifications: key decision problems and their complexities
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-103
-
- Article
- Export citation
Observing the superposition of a single particle with the vacuum
-
- Published online by Cambridge University Press:
- 08 November 2010, pp. 1051-1065
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MSC volume 20 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Paper
Weak bisimulations for the Giry monad†
-
- Published online by Cambridge University Press:
- 27 October 2010, pp. 781-798
-
- Article
- Export citation
Long-run cost analysis by approximation of linear operators over dioids
-
- Published online by Cambridge University Press:
- 03 June 2010, pp. 589-624
-
- Article
- Export citation
Domain theoretic characterisations of quasi-metric completeness in terms of formal balls†
-
- Published online by Cambridge University Press:
- 07 April 2010, pp. 453-472
-
- Article
- Export citation
Some reasons for generalising domain theory
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 239-265
-
- Article
- Export citation
The limit–colimit coincidence theorem for
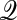 -categories
-categories
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 267-284
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
MSC volume 20 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Paper
A solution of the uniform word problem for ortholattices
-
- Published online by Cambridge University Press:
- 27 May 2010, pp. 625-638
-
- Article
- Export citation
Diamond embeddings into the enumeration degrees
-
- Published online by Cambridge University Press:
- 27 October 2010, pp. 799-811
-
- Article
- Export citation
Towards a typed Geometry of Interaction
-
- Published online by Cambridge University Press:
- 21 April 2010, pp. 473-521
-
- Article
- Export citation
The Travelling Salesman Problem for finite-sized cities†
-
- Published online by Cambridge University Press:
- 08 November 2010, pp. 1067-1078
-
- Article
- Export citation
Tilings: simulation and universality
-
- Published online by Cambridge University Press:
- 27 October 2010, pp. 813-850
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MSC volume 20 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 May 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Paper
Continuous-time quantum walks on the threshold network model
-
- Published online by Cambridge University Press:
- 08 November 2010, pp. 1079-1090
-
- Article
- Export citation
Diagrammatic logic applied to a parameterisation process
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 639-654
-
- Article
- Export citation
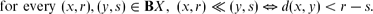
 -categories
-categories