Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T08:18:27.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate Kernel Clustering

Part of: Algorithms - Computer Science

Published online by Cambridge University Press:  21 December 2009

Subhash Khot  and
Assaf Naor
Subhash Khot
Affiliation:
Subhash Khot, Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, U.S.A., E-mail: khot@cims.nyu.edu
Assaf Naor
Affiliation:
Assaf Naor, Courant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, U.S.A., E-mail: naor@cims.nyu.edu
Get access

Abstract

In the kernel clustering problem we are given a large n × n positive-semidefinite matrix A = (aij) with 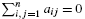and a small k × k positive-semidefinite matrix B = (bij). The goal is to find a partition S1, …, Sk of {1, … n} which maximizes the quantity

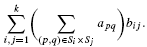
We study the computational complexity of this generic clustering problem which originates in the theory of machine learning. We design a constant factor polynomial time approximation algorithm for this problem, answering a question posed by Song et al. In some cases we manage to compute the sharp approximation threshold for this problem assuming the unique games conjecture (UGC). In particular, when B is the 3 × 3 identity matrix the UGC hardness threshold of this problem is exactly 16π/27. We present and study a geometric conjecture of independent interest which we show would imply that the UGC threshold when B is the k × k identity matrix is (8π/9)(1 – 1/k) for every k ≥ 3.

MSC classification

Secondary: 68W25: Approximation algorithms
Type
Research Article
Information
Mathematika , Volume 55 , Issue 1-2 , December 2009 , pp. 129 - 165
Copyright
Copyright © University College London 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alonn, N., Makarychev, K., Makarychev, Y. and Naor, A., Quadratic forms on graphs. Invent. Math. 163(3) (2006), 499–522.CrossRefGoogle Scholar
2.Alon, N. and Naor, A., Approximating the cut-norm via Grothendieck's inequality. SIAM J. Comput. 35(4) (2006), 787–803 (electronic).CrossRefGoogle Scholar
3.Arora, S., Berger, E., Kindler, G., Hazan, E. and Safra, S., On non-approximability for quadratic programs. In 46th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press (Los Alamitos, CA, 2005), 206–215.Google Scholar
4.Bansal, N., Blum, A. and Chawla, S., Correlation clustering. In 43rd Symposium on Foundations of Computer Science, IEEE Computer Society Press (Los Alamitos, CA, 2002), 238–247.Google Scholar
5.Charikar, M., Makarychev, K. and Makarychev, Y., Near-optimal algorithms for unique games (extended abstract). In STOC'06: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, ACM Press (New York, 2006), 205–214.CrossRefGoogle Scholar
6.Charikar, M., Makarychev, K. and Makarychev, Y., Near-optimal algorithms for maximum constraint satisfaction problems. In SODA '07: Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics (Philadelphia, PA, 2007), 62–68.Google Scholar
7.Charikar, M. and Wirth, A., Maximizing quadratic programs: extending Grothendieck's inequality. In 45th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press (Los Alamitos, CA, 2004), 54–60.CrossRefGoogle Scholar
8.Danzer, L., Grünbaum, B. and Klee, V., Helly's Theorem and its Relatives (Proceedings of Symposia in Pure Mathematics VII), American Mathematical Society (Providence, RI, 1963), 101–180.CrossRefGoogle Scholar
9.Feige, U., Kindler, G. and O'Donnell, R., Understanding parallel repetition requires understanding foams. In IEEE Conference on Computational Complexity, IEEE Computer Society Press (Los Alamitos, CA, 2007), 179–192.Google Scholar
10.Frieze, A. and Jerrum, M., Improved approximation algorithms for MAX k-CUT and MAX BISECTION. Algorithmica 18(1) (1997), 67–81.CrossRefGoogle Scholar
11.Gritzmann, P. and Klee, V., Inner and outer j-radii of convex bodies in finite-dimensional normed spaces. Discrete Comput. Geom. 7(3) (1992), 255–280.CrossRefGoogle Scholar
12.Håstad, J., Some optimal inapproximability results. J. ACM 48(4) (2001), 798–859 (electronic).CrossRefGoogle Scholar
13.Jung, H. W. E., über die kleinste kügel, die einerumliche figureinschlisst. J. Reine Angew. Math. 123 (1901), 241–257.Google Scholar
14.Khot, S., On the power of unique 2-prover 1-round games. In Proceedings of the 34th Annual ACM Symposium on Theory of Computing, ACM Press (New York, 2002), 767–775 (electronic).Google Scholar
15.Khot, S., Kindler, G., Mossel, E. and O'Donnell, R., Optimal inapproximability results for max-cut and other 2-variable csps? In 45th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press (Los Alamitos, CA, 2004), 146–154.CrossRefGoogle Scholar
16.Khot, S., Kindler, G., Mossel, E. and O'Donnell, R., Optimal inapproximability results for MAX-CUT and other 2-variable CSPs?. SIAM J. Comput. 37(1) (2007), 319–357 (electronic).CrossRefGoogle Scholar
17.Mossel, E., O'Donnell, R. and Oleszkiewicz, K., Noise stability of functions with low influences: invariance and optimality. In 46th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press (Los Alamitos, CA, 2005), 21–30.Google Scholar
18.Nemirovski, A., Roos, C. and Terlaky, T., On maximization of quadratic form over intersection of ellipsoids with common center. Math. Program 86(3 Ser. A) (1999), 463–473.CrossRefGoogle Scholar
19.Nesterov, Y., Semidefinite relaxation and nonconvex quadratic optimization. Optim. Methods Softw. 9(1–3) (1998), 141–160.CrossRefGoogle Scholar
20.Raghavendra, P., Optimal algorithms and inapproximability results for every csp?. In Proceedings of the 40th Annual ACM Symposium on Theory of Computing, ACM Press (New York, 2008), 245–254.Google Scholar
21.Rietz, R. E., A proof of the Grothendieck inequality. Israel J. Math. 19 (1974), 271–276.CrossRefGoogle Scholar
22.Rotar', V. I., Limit theorems for polylinear forms. J. Multivariate Anal. 9(4) (1979), 511–530.CrossRefGoogle Scholar
23.Scholkopf, B. and Smola, A. J., Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, MIT Press (Cambridge, MA, 2001).Google Scholar
24.Song, L., Smola, A., Gretton, A. and Borgwardt, K. A., A dependence maximization view of clustering. In Proceedings of the 24th International Conference on Machine Learning, Omnipress (Madison, WI, 2007), 815–822.CrossRefGoogle Scholar