Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Conway, J. H.
and
Sloane, N. J. A.
1983.
The Coxeter–Todd lattice, the Mitchell group, and related sphere packings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 93,
Issue. 3,
p.
421.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Litsyn, S. N.
and
Tsfasman, M. A.
1987.
Constructive high-dimensional sphere packings.
Duke Mathematical Journal,
Vol. 54,
Issue. 1,
Calderbank, A.
and
Sloane, N.
1987.
New trellis codes based on lattices and cosets.
IEEE Transactions on Information Theory,
Vol. 33,
Issue. 2,
p.
177.
Forney, G.D.
1988.
Coset codes. II. Binary lattices and related codes.
IEEE Transactions on Information Theory,
Vol. 34,
Issue. 5,
p.
1152.
Alon, Noga
1997.
Packings with large minimum kissing numbers.
Discrete Mathematics,
Vol. 175,
Issue. 1-3,
p.
249.
Forney, G.D.
Trott, M.D.
and
Sae-Young Chung
2000.
Sphere-bound-achieving coset codes and multilevel coset codes.
IEEE Transactions on Information Theory,
Vol. 46,
Issue. 3,
p.
820.
Sadeghi, M.-R.
Banihashemi, A.H.
and
Panario, D.
2006.
Low-Density Parity-Check Lattices: Construction and Decoding Analysis.
IEEE Transactions on Information Theory,
Vol. 52,
Issue. 10,
p.
4481.
Chen, Hao
2013.
On a generalization of Craig lattices.
Journal de théorie des nombres de Bordeaux,
Vol. 25,
Issue. 1,
p.
59.
Vlăduţ, Serge
2019.
Lattices with exponentially large kissing numbers.
Moscow Journal of Combinatorics and Number Theory,
Vol. 8,
Issue. 2,
p.
163.
Vlăduţ, Serge
2021.
On the Lattice Hadwiger Number of Superballs and Some Other Bodies.
Discrete & Computational Geometry,
Vol. 66,
Issue. 3,
p.
1105.

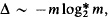 , as
, as 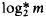 is the smallest value of
is the smallest value of 