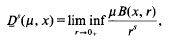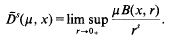Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mörters, P.
1997.
Average densities and linear rectifiability of measures.
Mathematika,
Vol. 44,
Issue. 2,
p.
313.
Mörters, Peter
1998.
Average Densities, Tangent Measures and Rectifiability.
Periodica Mathematica Hungarica,
Vol. 37,
Issue. 1-3,
p.
65.
Mörters, Peter
1998.
Symmetry Properties of Average Densities and Tangent Measure Distributions of Measures on the Line.
Advances in Applied Mathematics,
Vol. 21,
Issue. 1,
p.
146.
Mörters, Peter
1998.
The average density of the path of planar Brownian motion.
Stochastic Processes and their Applications,
Vol. 74,
Issue. 1,
p.
133.
Mörters, Peter
and
Shieh, Narn-Rueih
1999.
Small Scale Limit Theorems for the Intersection Local Times of Brownian Motion.
Electronic Journal of Probability,
Vol. 4,
Issue. none,