No CrossRef data available.
Article contents
Uniform distribution in compact groups
Published online by Cambridge University Press: 26 February 2010
Abstract
In a compact group G, a sequence (Fn) of finite sets is uniformly distributed if the averaging operators

are uniformly convergent to the mean for continuous complex-valued functions f. In any compact metric group, there are uniformly distributed sequences of finite sets which are determined by a metric for the group. In some compact groups, there are uniformly distributed sequences of finite sets which are determined by the algebraic structure. A necessary and sufficient condition for a sequence of finite sets to be uniformly distributed in a compact metric group is that for any metric d for G and each εG, there is a sequence of one-to-one maps pn: Fn→ Fn such that
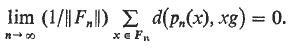
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1976

