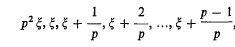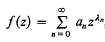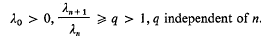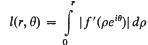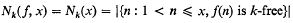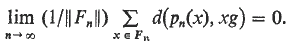Contents
Research Article
Incomplete Gauss sums
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-135
-
- Article
- Export citation
On a theorem of Davenport concerning continued fractions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-141
-
- Article
- Export citation
Bounded analytic functions with Hadamard gaps
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-146
-
- Article
- Export citation
The length of ray-images under starlike mappings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-150
-
- Article
- Export citation
Non-isomorphic projective sets
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-155
-
- Article
- Export citation
On Minkowski reduction of positive quaternary quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 156-158
-
- Article
- Export citation
Power free values of polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 159-183
-
- Article
- Export citation
Sprindžuk's theorem and Hausdorff dimension
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 184-197
-
- Article
- Export citation
Uniform distribution in compact groups
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-207
-
- Article
- Export citation
Structure of analytic Hausdorff spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 208-211
-
- Article
- Export citation
Eine Erweiterung der Croftonschen Formeln für konvexe Körper
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 212-219
-
- Article
- Export citation
The class number of pure fields of prime degree
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 220-226
-
- Article
- Export citation
Corrigendum
Corrigendum to:“A lattice-point problem in hyperbolic space”
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 227
-
- Article
-
- You have access
- Export citation
Index
Index to volume 23
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 228
-
- Article
- Export citation
Front matter
MTK volume 23 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
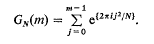
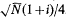 . A sharp estimate is given for max |
. A sharp estimate is given for max |