Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nair, M.
1976.
Power free values of polynomials.
Mathematika,
Vol. 23,
Issue. 2,
p.
159.
Heath-Brown, D. R.
1981.
Representation of an integer as a prime plus a product of two small factors.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 89,
Issue. 1,
p.
29.
Perelli, A.
Pintz, J.
and
Salerno, S.
1985.
Bombieri's theorem in short intervals. II.
Inventiones Mathematicae,
Vol. 79,
Issue. 1,
p.
1.
Harman, Glyn
1985.
Diophantine approximation with almost‐primes and sums of two squares.
Mathematika,
Vol. 32,
Issue. 2,
p.
301.
Tao, Zhan
1989.
Bombieri's theorem in short intervals.
Acta Mathematica Sinica,
Vol. 5,
Issue. 1,
p.
37.
Wu, Jie
1993.
Distribution des nombres ℬ-libres dans de petits intervalles.
Journal de théorie des nombres de Bordeaux,
Vol. 5,
Issue. 1,
p.
151.
Friedlander, J.
and
Goldston, D.
1997.
Sums of Three or More Primes.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 1,
p.
287.
Wu, J.
1998.
Primes of the form 𝑝=1+𝑚²+𝑛² in short intervals.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 1,
p.
1.
Alon, Noga
Rónyai, Lajos
and
Szabó, Tibor
1999.
Norm-Graphs: Variations and Applications.
Journal of Combinatorial Theory, Series B,
Vol. 76,
Issue. 2,
p.
280.
Axenovich, Maria
Füredi, Zoltán
and
Mubayi, Dhruv
2000.
On Generalized Ramsey Theory: The Bipartite Case.
Journal of Combinatorial Theory, Series B,
Vol. 79,
Issue. 1,
p.
66.
Mubayi, Dhruv
2003.
Coloring with three‐colored subgraphs.
Journal of Graph Theory,
Vol. 42,
Issue. 3,
p.
193.
KOSTOCHKA, A.
KUMBHAT, M.
and
ŁUCZAK, T.
2012.
Conflict-Free Colourings of Uniform Hypergraphs With Few Edges.
Combinatorics, Probability and Computing,
Vol. 21,
Issue. 4,
p.
611.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
307.
Füredi, Zoltán
and
Simonovits, Miklós
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
169.
Peng, Xing
and
Timmons, Craig
2014.
Infinite Turán Problems for Bipartite Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 28,
Issue. 2,
p.
702.
Koukoulopoulos, Dimitris
2015.
Primes in short arithmetic progressions.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1499.
Harman, Glyn
2016.
PRIMES IN BEATTY SEQUENCES IN SHORT INTERVALS.
Mathematika,
Vol. 62,
Issue. 2,
p.
572.
THORNER, JESSE
2016.
A variant of the Bombieri–Vinogradov theorem in short intervals and some questions of Serre.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 161,
Issue. 1,
p.
53.
Maynard, James
2016.
Dense clusters of primes in subsets.
Compositio Mathematica,
Vol. 152,
Issue. 7,
p.
1517.
Yao, Yanjun
2018.
Bombieri-type theorems for exponential sums over primes in short intervals and its application.
The Ramanujan Journal,
Vol. 46,
Issue. 2,
p.
525.

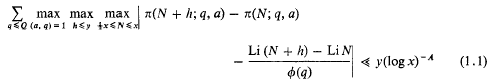
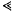 denotes as usual the suppression of an absolute constant,
denotes as usual the suppression of an absolute constant, 