Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:55:32.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete parabolic representations of link groups

Published online by Cambridge University Press:  26 February 2010

Robert Riley
Robert Riley
Affiliation:
The University of Southampton, Southampton SO9 5NH, England
Get access

Extract

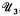Let k be a knot of type K and with group πK. Let θ: nK → PSL(ℂ) = PSL (2, ℂ) be a parabolic representation (p-rep) as defined in [14]. We shall call the representation discrete when its image πKθ is a discrete subgroup of PSL(ℂ). It is known that PSL(ℂ) can be identified with the group of orientation preserving isometries of hyperbolic 3-space , and that each discrete subgroup of PSL(ℂ) acts discontinuously on 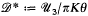. Hence each discrete p-rep θ has an associated orbit space . The present paper is a study of the general relations between the algebraic properties of a discrete image πKθ and the geometric properties of its orbit space.

Type
Research Article
Information
Mathematika , Volume 22 , Issue 2 , December 1975 , pp. 141 - 150
Copyright
Copyright © University College London 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Armstrong, M. A.. “The fundamental group of the orbit space of a discontinuous group” Proc. Cambridge Philos. Soc, 64 (1968), 299–301.CrossRefGoogle Scholar
2.Beardon, A. F. and Maskit, B.. “Limit points of kleinian groups and finite sided fundamental polyhedra”, Acta Math., 132 (1974), 1–12.CrossRefGoogle Scholar
3.Feustel, C. D.. “The torus theorem and some of its applications”, to appear.Google Scholar
4.Ford, L. R.. Automorphic functions, 2nd ed. (Chelsea, New York, 1951).Google Scholar
5.Greenberg, L.. “Fundamental polygons for Fuchsian groups”, J. Analyse Math., 18 (1967), 99–105.CrossRefGoogle Scholar
6.Kra, I.. Automorphic forms and Kleinian groups (W. A. Benjamin Inc., Mass., 1972).Google Scholar
7.Kronecker, L.. “Zwei Satze iiber Gleichungen mit ganzzahlen Coefficienten”, J. Reine Angew. Math., 53 (1857), 173–175.Google Scholar
8.Lehner, J.. Discontinuous groups and automorphic functions, Mathematical Surveys VIII (A.M.S Providence, 1964).CrossRefGoogle Scholar
9.Lyndon, R. and Ullman., J. “Groups generated by two parabolic linear fractional transformations”, Canad. J. Math., 22 (1970), 1388–1403.Google Scholar
10.Marden, A.. “The geometry of finitely generated kleinian groups”, Ann. of Math., 99 (1974), 383–462.CrossRefGoogle Scholar
11.Margulis, G. A.. “Isometry of closed manifolds of constant negative curvature with the same fundamental group”, Soviet Math. Dokl, 11 (1970), 722–723.Google Scholar
12.Maskit, B.. “On Poincare's theorem for fundamental polygons”, Adv. in Math., 1 (1971), 219–230.CrossRefGoogle Scholar
13.Milnor, J.. Morse theory, Annals of Mathematics Studies no. 51 (Princeton Univ. Press, Princeton, 1963).Google Scholar
14.Riley, R.. “Parabolic representations of knot groups, I”, Proc. London Math. Soc, (3), 24 (1972), 217–242.CrossRefGoogle Scholar
15.Riley, R.. “Hecke invariants of knot groups”, Glasgow Math. J., 15 (1974), 17–26.CrossRefGoogle Scholar
16.Riley, R.. “A quadratic parabolic group”, Math. Proc. Cambridge Phil. Soc, 11 (1975), 281–288.CrossRefGoogle Scholar
17.Riley, R.. “Parabolic representations of knot groups, II”, Proc. London Math. Soc, to appear.Google Scholar
18.Riley, R.. “Cubic parabolic groups”, in course of preparation.Google Scholar
19.Riley, R.. “Automorphisms of excellent link groups”, in course of preparation.Google Scholar
20.Seifert, H. and , Threlfall. Lehrbuch der Topologie (Chelsea, New York).Google Scholar
21.Shimizu, H.. “On discontinuous groups acting on the product of the upper half planes” Annals of Math., 11 (1963), 33–71.CrossRefGoogle Scholar
22.Waldhausen, F.. “On irreducible 3–manifolds which are sufficiently large”, Annals of Math., 87 (1968), 56–88.CrossRefGoogle Scholar
23.Weiss, E.. Algebraic number theory (McGraw-Hill, New York, 1963).Google Scholar
24.Wolf, J. A.. Spaces of constant curvature (McGraw-Hill, New York, 1967).Google Scholar