Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ball, Adam
and
Marcolli, Matilde
2016.
Spectral action models of gravity on packed swiss cheese cosmology.
Classical and Quantum Gravity,
Vol. 33,
Issue. 11,
p.
115018.

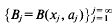 be a sequence of mutually disjoint open balls, with centres
be a sequence of mutually disjoint open balls, with centres 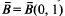 in
in 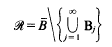
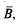 the balls {
the balls { provided that λ(ℛ)=0, where λ denotes the
provided that λ(ℛ)=0, where λ denotes the 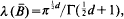 henceforth denoted by
henceforth denoted by 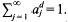 Larman [11] has noted that, under these circumstances, one also has
Larman [11] has noted that, under these circumstances, one also has 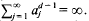 .
.