Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T21:41:04.230Z Has data issue: false hasContentIssue false
  • English
  • Français

The Exact Distribution of the Number of Vertices of a Random Convex Chain

Part of: General convexity

Published online by Cambridge University Press:  21 December 2009

Christian Buchta
Christian Buchta
Affiliation:
Fachbereich Mathematik, Universität Salzburg, Hellbrunner Straße 34, A-5020 Salzburg, Austria.
Get access

Abstract

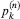Assume that n points P1,…,Pn are distributed independently and uniformly in the triangle with vertices (0, 1), (0, 0), and (1, 0). Consider the convex hull of (0, 1), P1,…,Pn, and (1, 0). The vertices of the convex hull form a convex chain. Let be the probability that the convex chain consists – apart from the points (0, 1) and (1, 0) – of exactly k of the points P1,…,Pn. Bárány, Rote, Steiger, and Zhang [3] proved that 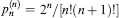. The values of 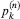are determined for k = 1,…,n − 1, and thus the distribution of the number of vertices of a random convex chain is obtained. Knowing this distribution provides the key to the answer of some long-standing questions in geometrical probability.

MSC classification

Secondary: 52A22: Random convex sets and integral geometry
Type
Research Article
Information
Mathematika , Volume 53 , Issue 2 , December 2006 , pp. 247 - 254
Copyright
Copyright © University College London 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alagar, V. S., On the distribution of a random triangle. J. Appl. Prob. 14 (1977), 284–297.CrossRefGoogle Scholar
2Bárány, I. and Reitzner, M., Random polytopes (manuscript).Google Scholar
3Bárány, I., Rote, G., Steiger, W. and Zhang, C.-H., A central limit theorem for convex chains in the square. Discrete Comput. Geom. 23 (2000), 35–50.CrossRefGoogle Scholar
4Buchta, C., Zufallspolygone in konvexen Vielecken. J. reine angew. Math. 347 (1984), 212–220.Google Scholar
5Buchta, C., On a conjecture of R. E. Miles about the convex hull of random points. Monatsh. Math. 102 (1986), 91–102.CrossRefGoogle Scholar
6Buchta, C., On the distribution of the number of vertices of random polygon. Anz. Österr. Akad. Wiss., Math.-Naturwiss. Kl., Abt. II, 139 (2003), 17–19.Google Scholar
7Buchta, C., An identity relating moments of functionals of convex hulls. Discrete Comput. Geom. 33 (2005), 125–142.CrossRefGoogle Scholar
8Henze, N., Random triangles in convex regions. J. Appl. Prob. 20 (1983), 111–125.CrossRefGoogle Scholar
9Reed, W. J., Random points in a simplex. Pacific J. Math. 54 (1974), 183–198.CrossRefGoogle Scholar
10Valtr, P., Probability that n random points are in convex position. Discrete Comput. Geom. 13 (1995), 637–643.CrossRefGoogle Scholar
11Valtr, P., The probability that n random points in a triangle are in convex position. Combinatorica 16 (1996), 567–573.CrossRefGoogle Scholar
12Vu, V. H., Sharp concentration of random polytopes. Geom. Funct. Anal. 15 (2005), 1284–1318.CrossRefGoogle Scholar