Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Knopfmacher, Arnold
and
Knopfmacher, John
1988.
The exact length of the Euclidean algorithm in [
X
]
.
Mathematika,
Vol. 35,
Issue. 2,
p.
297.
Knopfmacher, Arnold
and
Knopfmacher, John
1990.
Applications of Fibonacci Numbers.
p.
217.
Knopfmacher, Arnold
and
Knopfmacher, John
1991.
The number of steps in the euclidean algorithm over complex quadratic fields.
BIT,
Vol. 31,
Issue. 2,
p.
286.
Knopfmacher, Arnold
1991.
The length of the continued fraction expansion for a class of rational functions in .
Proceedings of the Edinburgh Mathematical Society,
Vol. 34,
Issue. 1,
p.
7.
Knopfmacher, Arnold
and
Mays, M. E.
1995.
Pierce Expansions of Ratios and Fibonacci and Lucas Numbers and Polynomials.
The Fibonacci Quarterly,
Vol. 33,
Issue. 2,
p.
153.
Enge, Andreas
2001.
The Extended Euclidian Algorithm on Polynomials, and the Computational Efficiency of Hyperelliptic Cryptosystems.
Designs, Codes and Cryptography,
Vol. 23,
Issue. 1,
p.
53.
2001.
Number Theory Arising From Finite Fields.
Flajolet, Philippe
2001.
D⋅E⋅K=(1000)8.
Random Structures & Algorithms,
Vol. 19,
Issue. 3-4,
p.
150.
Flajolet, P.
Gourdon, X.
and
Panario, D.
2001.
The Complete Analysis of a Polynomial Factorization Algorithm over Finite Fields.
Journal of Algorithms,
Vol. 40,
Issue. 1,
p.
37.
Panario, Daniel
2004.
Finite Fields and Applications.
Vol. 2948,
Issue. ,
p.
89.
Lhote, Loïck
and
Vallée, Brigitte
2008.
Gaussian Laws for the Main Parameters of the Euclid Algorithms.
Algorithmica,
Vol. 50,
Issue. 4,
p.
497.
Berthé, Valérie
Creusefond, Jean
Lhote, Loïck
and
Vallée, Brigitte
2013.
Multiple GCDs. probabilistic analysis of the plain algorithm.
p.
37.
Berthé, Valérie
Nakada, Hitoshi
Natsui, Rie
and
Vallée, Brigitte
2014.
Fine costs for Euclid's algorithm on polynomials and Farey maps.
Advances in Applied Mathematics,
Vol. 54,
Issue. ,
p.
27.
Berthé, Valérie
Lhote, Loïck
and
Vallée, Brigitte
2016.
Probabilistic analyses of the plain multiple gcd algorithm.
Journal of Symbolic Computation,
Vol. 74,
Issue. ,
p.
425.
Tongron, Yanapat
Kanasri, Narakorn Rompurk
and
Laohakosol, Vichian
2021.
The depth of continued fraction expansion for some classes of rational functions.
Asian-European Journal of Mathematics,
Vol. 14,
Issue. 03,
p.
2150033.
Berthé, Valérie
Nakada, Hitoshi
Natsui, Rie
and
Vallée, Brigitte
2021.
Analysis of generalized continued fraction algorithms over polynomials.
Finite Fields and Their Applications,
Vol. 73,
Issue. ,
p.
101849.

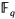 [
[