The concept of mixed invariant set is due to Bandt [1], Bedford [2], Dekking [3, 4], Marion [4] and Schulz [10]. An m-tuple B = (B1, …, Bm) of closed and bounded subsets Bi of a complete finitely compact (bounded and closed subsets are compact) metric space X is called a mixed invariant set with respect to contractions f1, …, fm and a transition matrix M = (mij), if, and only if,
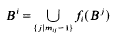
for every i ∈ {1, …, m}. In the papers quoted an essential condition is that all mappings f1, …, fm be contractions. We will show that, under certain conditions, the construction of mixed invariant sets also works in cases where some of the mappings are isometries or even expanding mappings.
 [X]
[X]