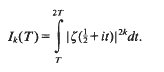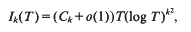Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Michel, Philippe
and
VanderKam, Jeffrey
2000.
Non-Vanishing of High Derivatives of Dirichlet L-Functions at the Central Point.
Journal of Number Theory,
Vol. 81,
Issue. 1,
p.
130.
Conrey, J. B.
and
Gonek, S. M.
2001.
High moments of the Riemann zeta-function.
Duke Mathematical Journal,
Vol. 107,
Issue. 3,
Soundararajan, Kannan
2009.
Moments of the Riemann zeta function.
Annals of Mathematics,
Vol. 170,
Issue. 2,
p.
981.
Zhang, Q.
2010.
On the Fourth Moment of the Riemann Zeta Function.
International Mathematics Research Notices,
Snaith, N. C.
2010.
Riemann Zeros and Random Matrix Theory.
Milan Journal of Mathematics,
Vol. 78,
Issue. 1,
p.
135.
Sono, Keiju
2012.
Lower bounds for the moments of the derivatives of the Riemann zeta-function and Dirichlet L-functions.
Lithuanian Mathematical Journal,
Vol. 52,
Issue. 4,
p.
420.
BUI, H. M.
2012.
NON-VANISHING OF DIRICHLET L-FUNCTIONS AT THE CENTRAL POINT.
International Journal of Number Theory,
Vol. 08,
Issue. 08,
p.
1855.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Radziwiłł, Maksym
and
Soundararajan, Kannan
2013.
CONTINUOUS LOWER BOUNDS FOR MOMENTS OF ZETA ANDL‐FUNCTIONS.
Mathematika,
Vol. 59,
Issue. 1,
p.
119.
Lubinsky, D. S.
2014.
Uniform Mean Value Estimates and Discrete Hilbert Inequalities VIA Orthogonal Dirichlet Series.
Acta Mathematica Hungarica,
Vol. 143,
Issue. 2,
p.
422.
Khan, Rizwanur
and
Ngo, Hieu
2016.
Nonvanishing of Dirichlet L-functions.
Algebra & Number Theory,
Vol. 10,
Issue. 10,
p.
2081.
Bettin, Sandro
Chandee, Vorrapan
and
Radziwiłł, Maksym
2017.
The mean square of the product of the Riemann zeta-function with Dirichlet polynomials.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2017,
Issue. 729,
p.
51.
Bui, H M
and
Milinovich, M B
2018.
Gaps between zeros of the Riemann zeta-function.
The Quarterly Journal of Mathematics,
Vol. 69,
Issue. 2,
p.
403.
Pratt, Kyle
2019.
Average nonvanishing of Dirichlet L-functions at
the central point.
Algebra & Number Theory,
Vol. 13,
Issue. 1,
p.
227.
Wu, Xiaosheng
2019.
The twisted mean square and critical zeros of Dirichlet L-functions.
Mathematische Zeitschrift,
Vol. 293,
Issue. 1-2,
p.
825.
Bui, Hung M.
Pratt, Kyle
Robles, Nicolas
and
Zaharescu, Alexandru
2020.
Breaking the 12-barrier for the twisted second moment of Dirichlet L-functions.
Advances in Mathematics,
Vol. 370,
Issue. ,
p.
107175.
Khan, Rizwanur
2024.
A reciprocity relation for the twisted second moment of the Riemann Zeta function.
Proceedings of the American Mathematical Society,
Vol. 153,
Issue. 1,
p.
81.
Page, Timothy
2026.
Unconditional lower bounds for the sixth and eighth moments of the Riemann zeta function.
Journal of Number Theory,
Vol. 280,
Issue. ,
p.
318.