Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T07:30:28.258Z Has data issue: false hasContentIssue false
  • English
  • Français

A minimal density plane covering problem

Published online by Cambridge University Press:  26 February 2010

H. G. Eggleston
H. G. Eggleston
Affiliation:
Bedford College, Regent's Park, London, N.W.1.
Get access

Extract

We say that a set of closed circular discs of radii r1r2, …, all lying in a Euclidean plane, is saturated if and only if r = inf ri > 0 and any circle of radius r has at least one point in common with a circle of the set. For any set X we use α(X) to denote the area of X. If X denotes the point set union of the discs and X(k) the part of X inside the disc whose centre is the origin and radius k then by the lower density of the covering we mean 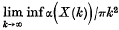. The problem is to find the exact lower bound of the lower density for any saturated set of circles. We show that it is φ/(6√3) provided the circles are disjoint. The general case, when they may overlap, remains unsolved.

Type
Research Article
Information
Mathematika , Volume 12 , Issue 2 , December 1965 , pp. 226 - 234
Copyright
Copyright © University College London 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Tóth, L. Fejes, Lagerungen in der Ebene, auf der Kugel und in Raum, Grundl. Math. Wiss. (Springer, Berlin, 1953).CrossRefGoogle Scholar