Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Davenport, H.
and
Halberstam, H.
1966.
The values of a trigonometrical polynomial at well spaced points.
Mathematika,
Vol. 13,
Issue. 1,
p.
91.
Elliott, P. D. T. A.
and
Halberstam, H.
1966.
Some applications of Bombieri's theorem.
Mathematika,
Vol. 13,
Issue. 2,
p.
196.
1966.
Small differences between prime numbers.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 293,
Issue. 1432,
p.
1.
Izumi, Masako
and
Izumi, Shin-ichi
1967.
On a theorem concerning trigonometrical polynomials.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 43,
Issue. 2,
Halberstam, H.
1967.
Footnote to the Titchmarsh-Linnik divisor problem.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 1,
p.
187.
Uchiyama, Saburô
1967.
On the representation of large even integers as sums of a prime and an almost prime, II.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 43,
Issue. 7,
Gallagher, P. X.
1967.
The large sieve.
Mathematika,
Vol. 14,
Issue. 1,
p.
14.
Burgess, D. A.
and
Elliott, P. D. T. A.
1968.
The average of the least primitive root.
Mathematika,
Vol. 15,
Issue. 1,
p.
39.
Gallagher, P. X.
1968.
Bombieri's mean value theorem.
Mathematika,
Vol. 15,
Issue. 1,
p.
1.
Miech, R. J.
1968.
On the equation 𝑛=𝑝+𝑥².
Transactions of the American Mathematical Society,
Vol. 130,
Issue. 3,
p.
494.
Wilson, Robin J.
1969.
The large sieve in algebraic number fields.
Mathematika,
Vol. 16,
Issue. 2,
p.
189.
Kátai, I.
1969.
On the distribution of arithmetical functions.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 20,
Issue. 1-2,
p.
69.
Bredihin, B. M.
Linnik, J. V.
and
Tschudakoff, N. G.
1969.
Number Theory and Analysis.
p.
23.
Rieger, G. J.
1969.
On polynomials and almost-primes.
Bulletin of the American Mathematical Society,
Vol. 75,
Issue. 1,
p.
100.
Wolke, Dieter
1969.
Moments of the number of classes of primitive quadratic forms with negative discriminant.
Journal of Number Theory,
Vol. 1,
Issue. 4,
p.
502.
Richert, H.-E.
1969.
Selberg's sieve with weights.
Mathematika,
Vol. 16,
Issue. 1,
p.
1.
Montgomery, H. L.
1969.
Zeros ofL-functions.
Inventiones Mathematicae,
Vol. 8,
Issue. 4,
p.
346.
Goldfeld, Morris
1969.
On the number of primes
p
for which
p+a
has a large prime factor
.
Mathematika,
Vol. 16,
Issue. 1,
p.
23.
Vaughan, R. C.
1970.
On a problem of Erdös, Straus and Schinzel.
Mathematika,
Vol. 17,
Issue. 2,
p.
193.
Kátai, I.
1970.
On an application of the large sieve: Shifted prime numbers, which have no prime divisors from a given arithmetical progression.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 21,
Issue. 1-2,
p.
151.

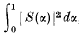 where
where 