Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bombieri, E.
1965.
On the large sieve.
Mathematika,
Vol. 12,
Issue. 2,
p.
201.
Davenport, H.
and
Halberstam, H.
1966.
The values of a trigonometrical polynomial at well spaced points.
Mathematika,
Vol. 13,
Issue. 1,
p.
91.
Gallagher, P. X.
1967.
The large sieve.
Mathematika,
Vol. 14,
Issue. 1,
p.
14.
Izumi, Masako
and
Izumi, Shin-ichi
1967.
On a theorem concerning trigonometrical polynomials.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 43,
Issue. 2,
Burgess, D. A.
and
Elliott, P. D. T. A.
1968.
The average of the least primitive root.
Mathematika,
Vol. 15,
Issue. 1,
p.
39.
Wolke, Dieter
1969.
Moments of the number of classes of primitive quadratic forms with negative discriminant.
Journal of Number Theory,
Vol. 1,
Issue. 4,
p.
502.
Wolke, Dieter
1970.
Farey-Br�che mit primem Nenner und das gro�e Sieb.
Mathematische Zeitschrift,
Vol. 114,
Issue. 2,
p.
145.
Halberstam, H.
and
Burgess, D. A.
1971.
Harold Davenport, 1907-1969.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 17,
Issue. ,
p.
159.
Montgomery, Hugh L.
1978.
The analytic principle of the large sieve.
Bulletin of the American Mathematical Society,
Vol. 84,
Issue. 4,
p.
547.
Lavrik, A F
1980.
A SURVEY OF LINNIK'S LARGE SIEVE AND THE DENSITY THEORY OF ZEROS OFL-FUNCTIONS.
Russian Mathematical Surveys,
Vol. 35,
Issue. 2,
p.
63.
Hildebrand, Adolf
1989.
Number Theory.
Vol. 1383,
Issue. ,
p.
76.
Vaughan, R. C.
1998.
Hardy's legacy to number theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 65,
Issue. 2,
p.
238.
Montgomery, Hugh L.
2001.
Twentieth Century Harmonic Analysis — A Celebration.
p.
271.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
307.
Kontorovich, Alex
2014.
Levels of Distribution and the Affine Sieve.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 23,
Issue. 5,
p.
933.
Vaughan, Robert C.
2016.
Open Problems in Mathematics.
p.
479.
Drappeau, Sary
Granville, Andrew
and
Shao, Xuancheng
2017.
SMOOTH‐SUPPORTED MULTIPLICATIVE FUNCTIONS IN ARITHMETIC PROGRESSIONS BEYOND THE ‐BARRIER.
Mathematika,
Vol. 63,
Issue. 3,
p.
895.
Diamond, Harold G.
2017.
Heini Halberstam, 1926-2014.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 6,
p.
1119.
Chen, William
and
Vaughan, Robert
2017.
Klaus Friedrich Roth. 29 October 1925 — 10 November 2015.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 63,
Issue. ,
p.
487.
Chen, William
and
Vaughan, Robert
2018.
Klaus Friedrich Roth, 1925-2015.
Bulletin of the London Mathematical Society,
Vol. 50,
Issue. 3,
p.
529.

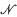 be a non-empty subset of the set of integers
be a non-empty subset of the set of integers