Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Myjak, Józef
Szarek, Tomasz
and
Śleçzka, Maciej
2006.
A Szpilrajn–Marczewski Type Theorem for Concentration Dimension on Polish Space.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 2,
p.
247.
Myjak, Józef
2007.
Differential Equations, Chaos and Variational Problems.
Vol. 75,
Issue. ,
p.
317.
Olsen, L.
2008.
Topological dimensions and multifractal Rényi dimensions of Polish spaces: a multifractal Szpilrajn type theorem.
Monatshefte für Mathematik,
Vol. 155,
Issue. 2,
p.
191.
KIHARA, TAKAYUKI
2019.
ON A METRIC GENERALIZATION OF THE tt-DEGREES AND EFFECTIVE DIMENSION THEORY.
The Journal of Symbolic Logic,
Vol. 84,
Issue. 2,
p.
726.

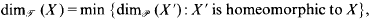
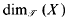 and
and 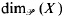 denote the topological and packing dimensions of
denote the topological and packing dimensions of 