Contents
Research Article
On effects of increasing amplitude in a boundary-layer spot
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-24
-
- Article
- Export citation
On the location of spectral concentration for Sturm–Liouville problems with rapidly decaying potential
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
-
- Article
- Export citation
No b-concentrated measures whenever 1<b≤2
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-41
-
- Article
- Export citation
A relationship between packing and topological dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 43-53
-
- Article
- Export citation
Hausdorff and packing dimensions and sections of measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-77
-
- Article
- Export citation
Semiselective coideals
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-103
-
- Article
- Export citation
Angelicity and the boundary problem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 105-112
-
- Article
- Export citation
Three space property for σ-fragmentability
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 113-118
-
- Article
- Export citation
On singular boundary points of complex functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-133
-
- Article
- Export citation
Ricci curvature and ends of Riemannian orbifolds
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-144
-
- Article
- Export citation
P-régularité de sommes d'exponentielles
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-175
-
- Article
- Export citation
Uniformity over primes of unramified splittings
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 177-189
-
- Article
- Export citation
Uniform bounds for the least almost-prime primitive root
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-207
-
- Article
- Export citation
Erratum
Erratum to “Bounds on the covering radius of a lattice”
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 209
-
- Article
-
- You have access
- Export citation
Book Reviews
M. Audin. Spinning Tops. Cambridge University Press. 1996, ISBN 0 521 56129 9, 139 pp., hardback, £25. - J. Barwise and L. Moss. Vicious Circles, On the Mathematics of non-wellfounded Phenomena. CSLI Lecture Notes No. 60. CSLI Publications. 1996, ISBN 1 57586 008 2, 390 pp., paperback, £16.95. - A. Beauville. Complex Algebraic Surfaces. Cambridge University Press. 1996, ISBN 0 521 49842 2, 132 pp., paperback, £13.95 - A. Borel. Automorphic forms on SL2(R). Cambridge Tracts in Mathematics No. 130. Cambridge University Press. 1997, ISBN 0 52158049 8, 192 pp., £32.50. - D. Bump. Automorphic Forms and Representations. Cambridge University Press. 1997, ISBN 0 521 55098 X, 574 pp., £65. - A. L. Carey and M. K. Murray, Editors. Geometric Analysis and Lie Theory in Mathematics and Physics. Cambridge University Press. 1998, ISBN 0 521 62490 8, 290 pp., paperback, £24.95. - K. Ciesielski. Set Theory for the Working Mathematician. LMS Student Texts No. 39. Cambridge University Press. 1997, ISBN 0 521 59465 0, 236 pp., paperback, £13.95. - R. Diestel. Graph Theory. Springer. 1997, ISBN 0 387 98211 6, 286 pp., softback, £22.50. - S. C. Ferry, A. Ranicki and J. Rosenberg, Editors. Novikov Conjectures, Index Theorems and Rigidity, Vols. 1 and 2. Cambridge University Press. Vol. 1, 1995, ISBN 0 521 49796 5, 372 pp., paperback, £24.95. Vol. 2, 1995, ISBN 0 521 49795 7, 364 pp., paperback, £24.95. - T. Frankel. The Geometry of Physics. Cambridge University Press. 1997, ISBN 0 521 38334 X, 654 pp., hardback, £65. - M. Gardner. The last recreations. Springer. 1997, ISBN 0 387 94929 1, 392 pp., £15.95. - C. C. Gillispie and F. L. Holmes, Editors. Biographical Dictionary of Mathematicians. Scribner's. 1997, ISBN 0 684 19282 9, 4 vols, 2696 pp., £200 the set. - V. Guillemin, E. Lerman and S. Sternberg. Symplectic Fibrations and Multiplicity Diagrams. Cambridge University Press. 1996, ISBN 0 521 44323 7, 222 pp., hardback, £29.95. - B. Hughes and A. Ranicki. Ends of Complexes. Cambridge University Press. 1996, ISBN 0 521 57625 3, 353 pp., hardback, £45. - E. I. Khukhro. p-Automorphisms of finite p-groups. LMS Lecture Note Series No. 246. Cambridge University Press. 1998, ISBN 0 521 59717 X, 204 pp., paperback, £24.95. - D. A. Klain and G.-C. Rota. Introduction to Geometric Probability. Accademia Nazionale dei Lincei (Cambridge University Press). 1997, ISBN 0 521 59654 8, 178 pp., paperback, £12.95. - W. Krawcewicz and Jianhong Wu. Theory of Degrees with Applications to Bifurcations and Differential Equations. Wiley. 1997, ISBN 0 471 15740 6, 374 pp., £75. - M. Lothaire. Combinatorics on Words. Cambridge Math. Library. Cambridge University Press. 1997, ISBN 0 521 59924 5, 238 pp., paperback, £17.95. - M. Pohst and H. Zassenhaus. Algorithmic Algebraic Number Theory. Cambridge University Press. 1997, ISBN 0 521 59669 6, 499 pp., paperback, £24.95. - R. Rashed, Editor. Encyclopedia of the History of Arabic Science, Vol. 2, Mathematics and the Physical Sciences. Routledge. 1996, ISBN 0 415 12411 5, 420 pp., £55 - R. W. Sharpe. Differential Geometry. Springer. 1996, ISBN 0 387 94732 9, 421 pp., £32.50. - C. B. Thomas, Editor. Contact and Symplectic Geometry. Cambridge University Press. 1996, ISBN 0 521 57086 7, 310 pp., hardback, £37.50.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 211-215
-
- Article
- Export citation
Front matter
MTK volume 45 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
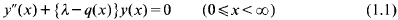
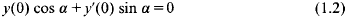
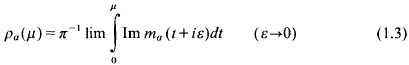
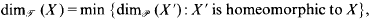
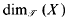 and
and 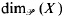 denote the topological and packing dimensions of
denote the topological and packing dimensions of 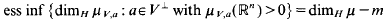
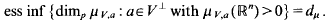
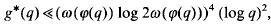
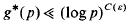
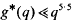 . However, there is not at present any stronger unconditional upper bound for
. However, there is not at present any stronger unconditional upper bound for