Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Coleman, M. D.
1998.
The normal density of prime ideals in small regions.
Monatshefte f�r Mathematik,
Vol. 125,
Issue. 2,
p.
111.
Coleman, M.D.
1999.
The Hooley–Huxley Contour Method for Problems in Number Fields.
Journal of Number Theory,
Vol. 74,
Issue. 2,
p.
250.
Harman, Glyn
and
Lewis, Philip
2001.
Gaussian primes in narrow sectors.
Mathematika,
Vol. 48,
Issue. 1-2,
p.
119.
Coleman, M. D.
2002.
The Hooley–Huxley contour method, for problems in number fields II: factorization and divisibility.
Mathematika,
Vol. 49,
Issue. 1-2,
p.
201.
Harman, G.
Kumchev, A.
and
Lewis, P.
2003.
The distribution of prime ideals of imaginary quadratic fields.
Transactions of the American Mathematical Society,
Vol. 356,
Issue. 2,
p.
599.
Baier, Stephan
and
Roy, Sayantan
2024.
A note on the distribution of prime idealsin real quadratic fields.
Functiones et Approximatio Commentarii Mathematici,
Vol. 71,
Issue. 2,

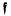 a fixed integral ideal and
a fixed integral ideal and 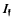 the group of fractional ideals of
the group of fractional ideals of 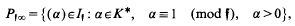
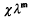 be an arbitrary Groessencharaktere mod f as defined in [15]. Then
be an arbitrary Groessencharaktere mod f as defined in [15]. Then 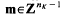 and, for
and, for 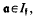
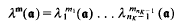
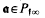 depends only on the
depends only on the 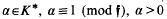 that exists such that
that exists such that 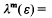 1 for all units ε in
1 for all units ε in 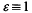 (mod
(mod