Let UK = [0, 1)K be the K-dimensional unit cube, where K ≥ 2. Suppose that we have a distribution ℘ of N points in UK. For × = ( x1, … , xK) ε UK, let A(x) denote the box
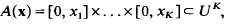
and write
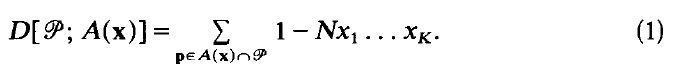
Note that since N is the cardinality of ℘ and x1 … xK is the K-dimensional volume of A(x), the term Nx1 … xK represents the “expected number” of, points of ℘ in A(x).