Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T18:15:47.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Clifford Algebras and Families of Abelian Varieties

Published online by Cambridge University Press:  22 January 2016

I. Satake
I. Satake*
Affiliation:
University of Chicago
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the arithmetic theory of automorphic functions on a symmetric bounded domain 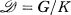= G/K, as developed recently by Shimura and Kuga [2], [2a], it is important to consider a family of (polarized) abelian varieties on 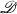obtained from a symplectic representation ρ (defined over Q) of G (viewed as an algebraic group defined over Q) satisfying a certain analyticity condition. Recently, I have determined completely such representations, reducing the problem to the case where G is a Q-simple group and where ρ is a Q-primary representation ([3], [4]). It has turned out that, besides the four standard solutions investigated already by Shimura, there exist two more non-standard solutions, one of which comes from a spin representation of the orthogonal group and thus gives a family of abelian varieties on a domain of type (IV). The purpose of this short note is to explain how one can construct most simply, starting from the “regular representation” of the corresponding Clifford algebra, examples of such families, including also the non-analytic case.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 27 , Issue 2 , July 1966 , pp. 435 - 446
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Chevalley, C. C., The algebraic theory of spinors, Columbia Univ. Press, New York, 1954.Google Scholar
[2] Kuga, M., Fiber varieties over a symmetric space whose fibers are abelian varieties, I, II, Lecture Notes, Univ. of Chicago, 1963–64.Google Scholar
[2 a] Kuga, M. and Shimura, G., On the zeta function of a fibre variety whose fibres are abelian varieties, Ann. of Math., 82 (1965), 478–539.Google Scholar
[3] Satake, I., Holomorphic imbeddings of symmetric domains into a Siegel space, Amer, J. of Math., 87 (1965), 425–461.CrossRefGoogle Scholar
[4] Satake, I., Symplectic representations of algebraic groups satisfying a certain analyticity condition, forthcoming.Google Scholar