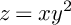1 Introduction
Let
![]() $(X,\omega )$
be a Stein Kähler manifold of complex dimension n, equipped with a holomorphic line bundle
$(X,\omega )$
be a Stein Kähler manifold of complex dimension n, equipped with a holomorphic line bundle
![]() $L \to X$
with smooth Hermitian metric
$L \to X$
with smooth Hermitian metric
![]() $e^{-\varphi }$
, and let
$e^{-\varphi }$
, and let
![]() $Z \subset X$
be a complex analytic subvariety of pure dimension d. To these data, assign the Hilbert spaces
$Z \subset X$
be a complex analytic subvariety of pure dimension d. To these data, assign the Hilbert spaces
 $$\begin{align*}{\mathscr B} _n (X, \varphi) := \left \{ F \in H^0(X,{\mathcal O} _X(L))\ ;\ ||F||^2_X := \int _{X} |F|^2 e^{-\varphi} \frac{\omega ^n}{n!} < +\infty \right \} \end{align*}$$
$$\begin{align*}{\mathscr B} _n (X, \varphi) := \left \{ F \in H^0(X,{\mathcal O} _X(L))\ ;\ ||F||^2_X := \int _{X} |F|^2 e^{-\varphi} \frac{\omega ^n}{n!} < +\infty \right \} \end{align*}$$
and
 $$\begin{align*}\mathfrak{B} _d (Z, \varphi) := \left \{ f \in H^0(Z,{\mathcal O} _Z(L))\ ;\ ||f||^2_Z := \int _{Z_{\mathrm{reg}}} |f|^2 e^{-\varphi} \frac{\omega ^d}{d!} < +\infty \right \}. \end{align*}$$
$$\begin{align*}\mathfrak{B} _d (Z, \varphi) := \left \{ f \in H^0(Z,{\mathcal O} _Z(L))\ ;\ ||f||^2_Z := \int _{Z_{\mathrm{reg}}} |f|^2 e^{-\varphi} \frac{\omega ^d}{d!} < +\infty \right \}. \end{align*}$$
Such Hilbert spaces are called (generalized) Bergman spaces. When the underlying manifold is
![]() $\mathbb {C}^n$
and the weight
$\mathbb {C}^n$
and the weight
![]() $\varphi $
is a Bargmann–Fock weight, the spaces are called (generalized) Bargmann–Fock spaces.
$\varphi $
is a Bargmann–Fock weight, the spaces are called (generalized) Bargmann–Fock spaces.
We say that Z is interpolating if the restriction map
induces a surjective map on Hilbert spaces. If the induced map
is surjective, then one says that Z is an interpolation subvariety, or simply interpolating with respect to
![]() $\varphi $
. It can be easily shown that if Z is interpolating, the map above is bounded.
$\varphi $
. It can be easily shown that if Z is interpolating, the map above is bounded.
In [Reference Pingali and VarolinPV2], Pingali and Varolin claimed that (Theorems 2 and 3) the (nonuniformly flat) curve
![]() $C_2=\{(x,y) \in \mathbb {C}^2 \ \vert \ xy^2=1\}$
and the surface
$C_2=\{(x,y) \in \mathbb {C}^2 \ \vert \ xy^2=1\}$
and the surface
![]() $S=\{(x,y,z)\in \mathbb {C}^3 \ \vert \ z=xy^2\}$
are interpolating with respect to a smooth weight
$S=\{(x,y,z)\in \mathbb {C}^3 \ \vert \ z=xy^2\}$
are interpolating with respect to a smooth weight
![]() $\varphi $
satisfying
$\varphi $
satisfying
![]() $m\omega _0 \leq \sqrt {-1}\partial \bar {\partial } \phi \leq M \omega _0$
, where
$m\omega _0 \leq \sqrt {-1}\partial \bar {\partial } \phi \leq M \omega _0$
, where
![]() $\omega _0$
is the Euclidean metric and
$\omega _0$
is the Euclidean metric and
![]() $m,M>0$
are positive constants. The purported proof of the claim rested heavily on Lemma 3.2, which aimed to generalize the QuimBo trick [Reference Berndtsson and Ortega CerdáBOC]. Unfortunately, Lemma 3.2 is false. (However, for Theorems 1 and 4, we do not need Lemma 3.2. Instead, Lemma 6 in [Reference LindholmL] in conjunction with elliptic regularity is enough.) In this erratum, we in fact prove that the negations of Theorems 2 and 3 in [Reference Pingali and VarolinPV2] are true.
$m,M>0$
are positive constants. The purported proof of the claim rested heavily on Lemma 3.2, which aimed to generalize the QuimBo trick [Reference Berndtsson and Ortega CerdáBOC]. Unfortunately, Lemma 3.2 is false. (However, for Theorems 1 and 4, we do not need Lemma 3.2. Instead, Lemma 6 in [Reference LindholmL] in conjunction with elliptic regularity is enough.) In this erratum, we in fact prove that the negations of Theorems 2 and 3 in [Reference Pingali and VarolinPV2] are true.
Theorem 1. The curve
![]() $C_2$
is not interpolating with respect to the Gaussian weight
$C_2$
is not interpolating with respect to the Gaussian weight
![]() $\vert x\vert ^2+\vert y\vert ^2$
.
$\vert x\vert ^2+\vert y\vert ^2$
.
Using Theorem 6.1 in [Reference Pingali and VarolinPV2], we can easily see that the following result holds.
Theorem 2. The surface S is not interpolating with respect to the Gaussian weight
![]() $\vert x\vert ^2+\vert y\vert ^2+\vert z \vert ^2$
.
$\vert x\vert ^2+\vert y\vert ^2+\vert z \vert ^2$
.
These results lead us to suspect that perhaps uniform flatness might be equivalent to being interpolating (with respect to the Gaussian weight) for smooth affine algebraic hypersurfaces. For smooth affine analytic hypersurfaces, this expectation is false as shown in [Reference Pingali and VarolinPV1].
2 Proof of Theorem 1
Let
![]() $f_n(x,y)=y^{-(2n+1)}$
, then
$f_n(x,y)=y^{-(2n+1)}$
, then
![]() $f_n \in \mathcal {O}(C_2)$
.
$f_n \in \mathcal {O}(C_2)$
.
Now,
 $$ \begin{align} ||f_n||^2&=\displaystyle \int_{C_2} |f_n(x,y)|^2e^{-(|x|^2+|y|^2)}dA \nonumber\\ &=\displaystyle \int_{\mathbb{C}^*}|y^{-(2n+1)}|^2e^{-(|y|^{-4}+|y|^2)}\left(1+4|y|^{-6}\right)dV(y)\nonumber\\ &=\pi \displaystyle \int_{r=0}^{\infty}r^{-(2n+1)}e^{-(r+r^{-2})}\left(1+4r^{-3}\right)dr. \end{align} $$
$$ \begin{align} ||f_n||^2&=\displaystyle \int_{C_2} |f_n(x,y)|^2e^{-(|x|^2+|y|^2)}dA \nonumber\\ &=\displaystyle \int_{\mathbb{C}^*}|y^{-(2n+1)}|^2e^{-(|y|^{-4}+|y|^2)}\left(1+4|y|^{-6}\right)dV(y)\nonumber\\ &=\pi \displaystyle \int_{r=0}^{\infty}r^{-(2n+1)}e^{-(r+r^{-2})}\left(1+4r^{-3}\right)dr. \end{align} $$
For
![]() $\frac {1}{2}<s<\frac {3}{2}$
and
$\frac {1}{2}<s<\frac {3}{2}$
and
![]() $\frac {1}{2}<t<\frac {3}{2}$
, let us consider the following integral:
$\frac {1}{2}<t<\frac {3}{2}$
, let us consider the following integral:
 $$ \begin{align*} \displaystyle \int_{0}^{\infty} e^{-(sr+tr^{-2})}4r^{-3}dr&=\left[ e^{-sr}\int e^{-tr^{-2}}4r^{-3}dr \right]_0^{\infty}-\int_0^{\infty}-se^{-sr} \left( \int e^{-tr^{-2}}4r^{-3}dr \right)dr\nonumber\\ &=\left[ e^{-sr}\frac{2}{t}e^{-tr^{-2}} \right]_0^{\infty}+\int_0^{\infty}se^{-sr} \frac{2}{t}e^{-tr^{-2}} dr\nonumber\\ &=\displaystyle \frac{2s}{t} \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \nonumber\\ \end{align*} $$
$$ \begin{align*} \displaystyle \int_{0}^{\infty} e^{-(sr+tr^{-2})}4r^{-3}dr&=\left[ e^{-sr}\int e^{-tr^{-2}}4r^{-3}dr \right]_0^{\infty}-\int_0^{\infty}-se^{-sr} \left( \int e^{-tr^{-2}}4r^{-3}dr \right)dr\nonumber\\ &=\left[ e^{-sr}\frac{2}{t}e^{-tr^{-2}} \right]_0^{\infty}+\int_0^{\infty}se^{-sr} \frac{2}{t}e^{-tr^{-2}} dr\nonumber\\ &=\displaystyle \frac{2s}{t} \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \nonumber\\ \end{align*} $$
Therefore, we have
 $$ \begin{align} \displaystyle \int_0^{\infty} e^{-(sr+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \left(1+ \frac{2s}{t}\right) \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \end{align} $$
$$ \begin{align} \displaystyle \int_0^{\infty} e^{-(sr+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \left(1+ \frac{2s}{t}\right) \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \end{align} $$
Differentiating (2) with respect to s, we arrive at the following:
 $$ \begin{align} \displaystyle \int_0^{\infty} -re^{-(sr+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \left(1+ \frac{2s}{t}\right) \int_0^{\infty} -re^{-(sr+tr^{-2})}dr+ \displaystyle \frac{2}{t} \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \end{align} $$
$$ \begin{align} \displaystyle \int_0^{\infty} -re^{-(sr+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \left(1+ \frac{2s}{t}\right) \int_0^{\infty} -re^{-(sr+tr^{-2})}dr+ \displaystyle \frac{2}{t} \int_0^{\infty} e^{-(sr+tr^{-2})}dr. \end{align} $$
Setting
![]() $s=1$
in (3), we have
$s=1$
in (3), we have
 $$ \begin{align} \displaystyle \int_0^{\infty} re^{-(r+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \int_0^{\infty} re^{-(r+tr^{-2})}dr+ \displaystyle \frac{2}{t} \int_0^{\infty}(r-1) e^{-(r+tr^{-2})}dr. \end{align} $$
$$ \begin{align} \displaystyle \int_0^{\infty} re^{-(r+tr^{-2})}\left( 1+4r^{-3}\right)dr=\displaystyle \int_0^{\infty} re^{-(r+tr^{-2})}dr+ \displaystyle \frac{2}{t} \int_0^{\infty}(r-1) e^{-(r+tr^{-2})}dr. \end{align} $$
Differentiating (4)
![]() $(n+1)$
times with respect to t, we see that
$(n+1)$
times with respect to t, we see that
 $$ \begin{align} &\displaystyle \int_0^{\infty} r\left( -r^{-2} \right)^{n+1}e^{-(r+tr^{-2})}\left( 1+4r^{-3}\right)dr \nonumber\\ &=\displaystyle \int_0^{\infty} r\left( -r^{-2} \right)^{n+1}e^{-(r+tr^{-2})}dr + 2\int_0^{\infty}(r-1) e^{-r} \frac{d^{n+1}}{dt^{n+1}}\left( \frac{e^{-tr^{-2}}}{t} \right)dr \nonumber \\ &=(-1)^{n+1} \displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+tr^{-2})}dr + 2(-1)^{n+1}\displaystyle\int_0^{\infty}(r-1) e^{-r} \sum\limits_{k=0}^{n+1}\frac{(n+1)!}{(n+1-k)!}\frac{r^{-2(n+1-k)}}{t^{k+1}}e^{-tr^{-2}}dr \nonumber\\ &=(-1)^{n+1} \displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+tr^{-2})}dr +2(-1)^{n+1}(n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+tr^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2(n+1-k)}}{(n+1-k)!}\frac{1}{t^{k+1}}dr. \nonumber\\ \end{align} $$
$$ \begin{align} &\displaystyle \int_0^{\infty} r\left( -r^{-2} \right)^{n+1}e^{-(r+tr^{-2})}\left( 1+4r^{-3}\right)dr \nonumber\\ &=\displaystyle \int_0^{\infty} r\left( -r^{-2} \right)^{n+1}e^{-(r+tr^{-2})}dr + 2\int_0^{\infty}(r-1) e^{-r} \frac{d^{n+1}}{dt^{n+1}}\left( \frac{e^{-tr^{-2}}}{t} \right)dr \nonumber \\ &=(-1)^{n+1} \displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+tr^{-2})}dr + 2(-1)^{n+1}\displaystyle\int_0^{\infty}(r-1) e^{-r} \sum\limits_{k=0}^{n+1}\frac{(n+1)!}{(n+1-k)!}\frac{r^{-2(n+1-k)}}{t^{k+1}}e^{-tr^{-2}}dr \nonumber\\ &=(-1)^{n+1} \displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+tr^{-2})}dr +2(-1)^{n+1}(n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+tr^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2(n+1-k)}}{(n+1-k)!}\frac{1}{t^{k+1}}dr. \nonumber\\ \end{align} $$
Substituting
![]() $t=1$
in (5), we get
$t=1$
in (5), we get
 $$ \begin{align} \displaystyle \int_0^{\infty} r^{-(2n+1)}e^{-(r+r^{-2})}\left( 1+4r^{-3}\right)dr=&\displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+r^{-2})}dr\quad \nonumber \\ &+ 2(n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr. \quad\end{align} $$
$$ \begin{align} \displaystyle \int_0^{\infty} r^{-(2n+1)}e^{-(r+r^{-2})}\left( 1+4r^{-3}\right)dr=&\displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+r^{-2})}dr\quad \nonumber \\ &+ 2(n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr. \quad\end{align} $$
Now,
 $$ \begin{align} &\displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+r^{-2})}dr \nonumber\\ &=\left[e^{-r}\int r^{-2(n-1)}e^{-r^{-2}}r^{-3}dr \right]_0^{\infty}-\int_{0}^{\infty}-e^{-r}\left(\int r^{-2(n-1)}e^{-r^{-2}}r^{-3}dr\right)dr \nonumber\\ &=\frac{(-1)^{n-1}}{2} \left[ e^{-r} \sum\limits_{k=0}^{n-1}(-1)^{n-1-k}\frac{(n-1)!}{k!}(-r^{-2})^ke^{-r^{-2}} \right]_{0}^{\infty}\nonumber\\ &\quad+\frac{(-1)^{n-1}}{2} \int_{0}^{\infty}e^{-r} \sum\limits_{k=0}^{n-1}(-1)^{n-1-k}\frac{(n-1)!}{k!}(-r^{-2})^ke^{-r^{-2}}dr\nonumber\\ &=\frac{(n-1)!}{2}\int_{0}^{\infty}e^{-(r+r^{-2})} \sum\limits_{k=0}^{n-1}\frac{r^{-2k}}{k!}dr\nonumber\\ &\leq \frac{(n-1)!}{2}\int_{0}^{\infty}e^{-(r+r^{-2})} e^{r^{-2}}dr.\nonumber\\ &\leq (n-1)! \end{align} $$
$$ \begin{align} &\displaystyle \int_0^{\infty} r^{-2n-1}e^{-(r+r^{-2})}dr \nonumber\\ &=\left[e^{-r}\int r^{-2(n-1)}e^{-r^{-2}}r^{-3}dr \right]_0^{\infty}-\int_{0}^{\infty}-e^{-r}\left(\int r^{-2(n-1)}e^{-r^{-2}}r^{-3}dr\right)dr \nonumber\\ &=\frac{(-1)^{n-1}}{2} \left[ e^{-r} \sum\limits_{k=0}^{n-1}(-1)^{n-1-k}\frac{(n-1)!}{k!}(-r^{-2})^ke^{-r^{-2}} \right]_{0}^{\infty}\nonumber\\ &\quad+\frac{(-1)^{n-1}}{2} \int_{0}^{\infty}e^{-r} \sum\limits_{k=0}^{n-1}(-1)^{n-1-k}\frac{(n-1)!}{k!}(-r^{-2})^ke^{-r^{-2}}dr\nonumber\\ &=\frac{(n-1)!}{2}\int_{0}^{\infty}e^{-(r+r^{-2})} \sum\limits_{k=0}^{n-1}\frac{r^{-2k}}{k!}dr\nonumber\\ &\leq \frac{(n-1)!}{2}\int_{0}^{\infty}e^{-(r+r^{-2})} e^{r^{-2}}dr.\nonumber\\ &\leq (n-1)! \end{align} $$
Using (1), (6), and (7), we can see that the following holds:
 $$ \begin{align} ||f_n||^2 \leq \pi (n-1)! +2\pi (n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr <\infty. \end{align} $$
$$ \begin{align} ||f_n||^2 \leq \pi (n-1)! +2\pi (n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr <\infty. \end{align} $$
Suppose
![]() $C_2$
is interpolating. Then, there exist
$C_2$
is interpolating. Then, there exist
![]() $F_n\in \mathscr {B}_2((|x|^2+|y|^2))$
and
$F_n\in \mathscr {B}_2((|x|^2+|y|^2))$
and
![]() $C>0$
such that
$C>0$
such that
![]() $F_n|_{C_2}=f_n$
and
$F_n|_{C_2}=f_n$
and
Let
 $$ \begin{align*} F_n(x,y)=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}x^iy^j. \end{align*} $$
$$ \begin{align*} F_n(x,y)=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}x^iy^j. \end{align*} $$
Then, we have
 $$ \begin{align} y^{-(2n+1)}&=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}y^{-2i}y^j\nonumber\\ &=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}y^{-(2i-j)}\nonumber\\ &=\displaystyle \sum\limits_{2i-j=2n+1}c_{ij}y^{-(2i-j)}.\nonumber\\ \end{align} $$
$$ \begin{align} y^{-(2n+1)}&=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}y^{-2i}y^j\nonumber\\ &=\displaystyle \sum\limits_{i,j \geq 0}c_{ij}y^{-(2i-j)}\nonumber\\ &=\displaystyle \sum\limits_{2i-j=2n+1}c_{ij}y^{-(2i-j)}.\nonumber\\ \end{align} $$
This equation implies that
 $$ \begin{align} \sum\limits_{k=1}^{\infty}c_{k+n,2k-1}=1. \end{align} $$
$$ \begin{align} \sum\limits_{k=1}^{\infty}c_{k+n,2k-1}=1. \end{align} $$
Equation (11) implies that there exists an
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $|c_{m+n,2m-1}|\geq 2^{-(m+1)}$
. Therefore,
$|c_{m+n,2m-1}|\geq 2^{-(m+1)}$
. Therefore,
 $$ \begin{align} ||F_n||^2&\geq \sum\limits_{k=1}^{\infty}|c_{k+n,2k-1}|^2(k+n)!(2k-1)!\nonumber\\& \geq |c_{m+n,2m-1}|^2(m+n)!(2m-1)!\nonumber\\& \geq (2^{-(m+1)})^2(1+n)!2^{2m-2}\nonumber\\& \geq \frac{(n+1)!}{2^4}. \end{align} $$
$$ \begin{align} ||F_n||^2&\geq \sum\limits_{k=1}^{\infty}|c_{k+n,2k-1}|^2(k+n)!(2k-1)!\nonumber\\& \geq |c_{m+n,2m-1}|^2(m+n)!(2m-1)!\nonumber\\& \geq (2^{-(m+1)})^2(1+n)!2^{2m-2}\nonumber\\& \geq \frac{(n+1)!}{2^4}. \end{align} $$
From (8), (9), and (12), we conclude that
 $$ \begin{align*} \frac{(n+1)!}{2^4} \leq C \left( \pi (n-1)! +2\pi (n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr \right). \end{align*} $$
$$ \begin{align*} \frac{(n+1)!}{2^4} \leq C \left( \pi (n-1)! +2\pi (n+1)!\displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr \right). \end{align*} $$
This inequality implies that
 $$ \begin{align*} \frac{1}{2^4} \leq \pi C \left( \frac{1}{n(n+1)} +2 \displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr \right). \end{align*} $$
$$ \begin{align*} \frac{1}{2^4} \leq \pi C \left( \frac{1}{n(n+1)} +2 \displaystyle\int_0^{\infty}(r-1) e^{-(r+r^{-2})}\sum\limits_{k=0}^{n+1}\frac{r^{-2k}}{k!}dr \right). \end{align*} $$
We are led to a contradiction because
 $\left ( \frac {1}{n(n+1)} +2 \displaystyle \int _0^{\infty }(r-1) e^{-(r+r^{-2})}\sum \limits _{k=0}^{n+1}\frac {r^{-2k}}{k!}dr \right ) \rightarrow 0$
, as
$\left ( \frac {1}{n(n+1)} +2 \displaystyle \int _0^{\infty }(r-1) e^{-(r+r^{-2})}\sum \limits _{k=0}^{n+1}\frac {r^{-2k}}{k!}dr \right ) \rightarrow 0$
, as
![]() $n \rightarrow \infty $
.
$n \rightarrow \infty $
.
![]() $\Box $
$\Box $