Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsushima, Yozô
1961.
Espaces Homogènes de Stein des Groupes de Lie Complexes, II.
Nagoya Mathematical Journal,
Vol. 18,
Issue. ,
p.
153.
Borel, Armand
and
Harish-Chandra
1961.
Arithmetic subgroups of algebraic groups.
Bulletin of the American Mathematical Society,
Vol. 67,
Issue. 6,
p.
579.
1962.
Vol. 12,
Issue. ,
p.
457.
Richardson, R. W.
1973.
The variation of isotropy subalgebras for analytic transformation groups.
Mathematische Annalen,
Vol. 204,
Issue. 1,
p.
83.
Barth, Wolf
and
Otte, Michael
1973.
Invariante holomorphe Funktionen auf reduktiven Liegruppen.
Mathematische Annalen,
Vol. 201,
Issue. 2,
p.
97.
Richardson, R. W.
1974.
Principal orbit types for reductive groups acting on stein manifolds.
Mathematische Annalen,
Vol. 208,
Issue. 4,
p.
323.
Takeuchi, Shigeru
1975.
On completeness of holomorphic principal bundles.
Nagoya Mathematical Journal,
Vol. 56,
Issue. ,
p.
121.
Sato, M.
and
Kimura, T.
1977.
A classification of irreducible prehomogeneous vector spaces and their relative invariants.
Nagoya Mathematical Journal,
Vol. 65,
Issue. ,
p.
1.
Nisnevich, E. A.
1977.
Affine homogeneous spaces and finite subgroups of arithmetic groups over function fields.
Functional Analysis and Its Applications,
Vol. 11,
Issue. 1,
p.
64.
Gilligan, B.
and
Huckleberry, A. T.
1978.
On non-compact complex nil-manifolds.
Mathematische Annalen,
Vol. 238,
Issue. 1,
p.
39.
1978.
Vol. 80,
Issue. ,
p.
587.
Gilligan, B.
and
Huckleberry, A.
1978.
Pseudoconcave homogeneous surfaces.
Commentarii Mathematici Helvetici,
Vol. 53,
Issue. 1,
p.
429.
Lassalle, Michel
1979.
Les orbites d'un espace hermitien sym�trique compact.
Inventiones Mathematicae,
Vol. 52,
Issue. 3,
p.
199.
Borho, Walter
and
Kraft, Hanspeter
1979.
Über Bahnen und deren Deformationen bei linearen Aktionen reduktiver Gruppen.
Commentarii Mathematici Helvetici,
Vol. 54,
Issue. 1,
p.
61.
Huckleberry, Alan T.
and
Oeljeklaus, Eberhard
1980.
A characterization of complex homogeneous cones.
Mathematische Zeitschrift,
Vol. 170,
Issue. 2,
p.
181.
Huckleberry, A. T.
and
Oeljeklaus, E.
1981.
Manifolds and Lie Groups.
p.
159.
Sugiura, Mitsuo
1981.
Manifolds and Lie Groups.
p.
405.
Snow, Dennis M.
1982.
Reductive group actions on Stein spaces.
Mathematische Annalen,
Vol. 259,
Issue. 1,
p.
79.
Gilligan, Bruce
1983.
Complex Analysis — Fifth Romanian-Finnish Seminar.
Vol. 1014,
Issue. ,
p.
27.
Borel, Armand
and
Harish-Chandra
1984.
Collected Papers.
p.
1227.


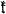 les algèbres de Lie de
les algèbres de Lie de 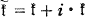 (
(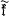 est une sous-algèbre complexe de g.
est une sous-algèbre complexe de g.