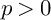1. Introduction
All over this paper, R denotes a discrete valuation ring with field of fractions K and residue field k of characteristic
![]() $p>0$
. In addition, schemes and log schemes are supposed to be locally Noetherian.
$p>0$
. In addition, schemes and log schemes are supposed to be locally Noetherian.
Let S be a regular scheme, and let
![]() $U \subseteq S$
be a dense open subset. Let
$U \subseteq S$
be a dense open subset. Let
![]() $f: X \to S$
be a finite flat morphism of schemes, unramified over U. The Zariski–Nagata purity theorem, known as purity of the branch locus, says that the closed subset of S where f ramifies is either empty or of pure codimension
$f: X \to S$
be a finite flat morphism of schemes, unramified over U. The Zariski–Nagata purity theorem, known as purity of the branch locus, says that the closed subset of S where f ramifies is either empty or of pure codimension
![]() $1$
. On the other hand, given a finite étale group scheme
$1$
. On the other hand, given a finite étale group scheme
![]() $G/S$
, and an fppf
$G/S$
, and an fppf
![]() $G_U$
-torsor
$G_U$
-torsor
![]() $X \to U$
(hence an étale torsor by fppf descent), if it extends into an fppf G-torsor over the whole S, it needs to be étale, hence unramified. But the purity theorem suggests that such an extension may not exist in general. Nevertheless, if the extension of the torsor
$X \to U$
(hence an étale torsor by fppf descent), if it extends into an fppf G-torsor over the whole S, it needs to be étale, hence unramified. But the purity theorem suggests that such an extension may not exist in general. Nevertheless, if the extension of the torsor
![]() $X \to U$
ramifies outside U, and if the ramification is tame, there might be a way to lift it into a log torsor over S. Indeed, assume that
$X \to U$
ramifies outside U, and if the ramification is tame, there might be a way to lift it into a log torsor over S. Indeed, assume that
![]() $D:=S\backslash U$
is a normal crossing divisor, so that one can endow S with the divisorial log structure induced by D. Then, logarithmic torsors over X are, roughly speaking, tamely ramified over D. This approach of extending torsors into log torsors has been followed in [Reference Mehidi11], and the main purpose of this paper is to enhance their results. The paper is divided into two independent parts, which we explain below.
$D:=S\backslash U$
is a normal crossing divisor, so that one can endow S with the divisorial log structure induced by D. Then, logarithmic torsors over X are, roughly speaking, tamely ramified over D. This approach of extending torsors into log torsors has been followed in [Reference Mehidi11], and the main purpose of this paper is to enhance their results. The paper is divided into two independent parts, which we explain below.
Part I:
Let C be a smooth projective curve over K, endowed with a K-point Q, and let J denote its Jacobian variety. Let
![]() $\mathcal {C}$
be a regular model of C over R, such that its special fiber is a normal crossing divisor, and endow
$\mathcal {C}$
be a regular model of C over R, such that its special fiber is a normal crossing divisor, and endow
![]() $\mathcal {C}$
with the canonical log structure induced by this divisor; let
$\mathcal {C}$
with the canonical log structure induced by this divisor; let
![]() $\mathcal {Q}$
denote the R-section extending Q by properness. Let G be a finite commutative group scheme over K. It is well known that the Jacobian variety classifies fppf commutative torsors, which can be rephrased through the one-to-one correspondence (cf. [Reference Mehidi11, lemme 2.3]):
$\mathcal {Q}$
denote the R-section extending Q by properness. Let G be a finite commutative group scheme over K. It is well known that the Jacobian variety classifies fppf commutative torsors, which can be rephrased through the one-to-one correspondence (cf. [Reference Mehidi11, lemme 2.3]):
where the group on the left is the first cohomology group classifying fppf pointed G-torsors (relatively to Q) over C, and
![]() $G^D$
is the Cartier dual of G. It is shown in [Reference Mehidi11, Rem. 1.11] that one has a similar correspondence for log torsors over
$G^D$
is the Cartier dual of G. It is shown in [Reference Mehidi11, Rem. 1.11] that one has a similar correspondence for log torsors over
![]() $\mathcal {C}$
. Indeed, if
$\mathcal {C}$
. Indeed, if
![]() $\mathcal {G}$
denotes a finite flat commutative R-group scheme, one has a one-to-one correspondence:
$\mathcal {G}$
denotes a finite flat commutative R-group scheme, one has a one-to-one correspondence:
where the group on the left is the first cohomology group classifying Kummer log flat pointed
![]() $\mathcal {G}$
-torsors (relatively to
$\mathcal {G}$
-torsors (relatively to
![]() $\mathcal {Q}$
) over
$\mathcal {Q}$
) over
![]() $\mathcal {C}$
, and
$\mathcal {C}$
, and
![]() $\mathrm {Pic}^{log}_{\mathcal {C}/R}$
is the relative log Picard functor of
$\mathrm {Pic}^{log}_{\mathcal {C}/R}$
is the relative log Picard functor of
![]() $\mathcal {C}/R$
. An immediate consequence of this is that, given a pointed fppf G-torsor over C, it extends into a log torsor over
$\mathcal {C}/R$
. An immediate consequence of this is that, given a pointed fppf G-torsor over C, it extends into a log torsor over
![]() $\mathcal {C}$
if and only if there exists a finite flat R-model
$\mathcal {C}$
if and only if there exists a finite flat R-model
![]() $\mathcal {G}$
of G such that the K-morphism
$\mathcal {G}$
of G such that the K-morphism
![]() $G^D \to J$
from (⋆) corresponding to the torsor extends into an R-morphism
$G^D \to J$
from (⋆) corresponding to the torsor extends into an R-morphism
![]() $\mathcal {G}^D \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
. Moreover, if
$\mathcal {G}^D \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
. Moreover, if
![]() $\mathcal {J}$
is the Néron model of J over R, it is shown in the same paper that the canonical map
$\mathcal {J}$
is the Néron model of J over R, it is shown in the same paper that the canonical map
![]() $J \hookrightarrow \mathrm {Pic}^{}_{{C}/R}$
extends uniquely into a map
$J \hookrightarrow \mathrm {Pic}^{}_{{C}/R}$
extends uniquely into a map
![]() $\mathcal {J} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
. In particular, if the morphism
$\mathcal {J} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
. In particular, if the morphism
![]() $G^D \to J$
extends into a morphism
$G^D \to J$
extends into a morphism
![]() $\mathcal {G}^D \to \mathcal {J}$
, the torsor extends into a
$\mathcal {G}^D \to \mathcal {J}$
, the torsor extends into a
![]() $\mathcal {G}$
-log torsor over
$\mathcal {G}$
-log torsor over
![]() $\mathcal {C}$
. In this paper, we want to invest the converse. Given that
$\mathcal {C}$
. In this paper, we want to invest the converse. Given that
![]() $\mathcal {J}$
is a smooth scheme, it is a nicer object to work with than the log Picard functor. Using the results of [Reference Molcho and Wise12] on log curves, we give a partial answer to this question:
$\mathcal {J}$
is a smooth scheme, it is a nicer object to work with than the log Picard functor. Using the results of [Reference Molcho and Wise12] on log curves, we give a partial answer to this question:
Corollary 3.4. Let C be a smooth projective semistable and geometrically connected curve endowed with a K-point. Let
![]() $\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure (cf. example 2.1(3)). Let G be a finite commutative K-group scheme, and let
$\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure (cf. example 2.1(3)). Let G be a finite commutative K-group scheme, and let
![]() $\mathcal {G}$
be a finite flat R-model of G. Then a pointed fppf G-torsor over C extends into a pointed
$\mathcal {G}$
be a finite flat R-model of G. Then a pointed fppf G-torsor over C extends into a pointed
![]() $\mathcal {G}$
-log torsor over
$\mathcal {G}$
-log torsor over
![]() $\mathcal {C}$
if and only if the K-morphism
$\mathcal {C}$
if and only if the K-morphism
![]() $G^D \to J$
associated with the generic torsor (cf. (⋆)) extends into an R-morphism
$G^D \to J$
associated with the generic torsor (cf. (⋆)) extends into an R-morphism
![]() $\mathcal {G}^D \to \mathcal {J}$
.
$\mathcal {G}^D \to \mathcal {J}$
.
Part II:
In the second part of this paper, we would like to drop the assumption that G admits a finite flat R-model. Indeed, there exist groups which do not admit such a model (cf. Example 3.7). However, if G is finite, then what is true in general is that it admits a quasi-finite flat R-model (cf. [Reference Antei and Emsalem2, Th. 3.7]). In the latter, the authors took advantage of this to obtain partial answers to the problem of extending finite torsors. In particular, they showed that there exists a modification (a Néron blow-up) of the regular model of the curve over which the torsor extends under some quasi-finite flat group scheme. On the other hand, under additional assumptions on R, it is shown in [Reference Phung and Santos16] that a torsor under a quasi-finite flat group scheme reduces into a torsor under a finite flat group scheme. Combining these two results, together with our previous work, we prove the following:
Theorem 4.4. Let C be a smooth projective and geometrically connected K-curve with a K-point Q. Let
![]() $\mathcal {C}$
be an R-regular model of C, and let G be a finite commutative K-group scheme. Let
$\mathcal {C}$
be an R-regular model of C, and let G be a finite commutative K-group scheme. Let
![]() $Y \to C$
be an fppf pointed G-torsor (relatively to Q). Then, there exists a quasi-finite flat group scheme
$Y \to C$
be an fppf pointed G-torsor (relatively to Q). Then, there exists a quasi-finite flat group scheme
![]() $\mathcal {G}$
over R with generic fiber G, and an fppf pointed
$\mathcal {G}$
over R with generic fiber G, and an fppf pointed
![]() $\mathcal {G}$
-torsor
$\mathcal {G}$
-torsor
![]() $\mathcal {Y} \to \mathcal {C}$
that extends the G-torsor
$\mathcal {Y} \to \mathcal {C}$
that extends the G-torsor
![]() $Y \to C$
.
$Y \to C$
.
2. Preliminaries
2.1. Kummer log flat torsors
2.1.1. Log schemes
Let
![]() $({X},\mathcal {O}_X)$
denote a scheme. A logarithmic (log) structure on X is the data of a sheaf of monoids
$({X},\mathcal {O}_X)$
denote a scheme. A logarithmic (log) structure on X is the data of a sheaf of monoids
![]() $M_X$
on
$M_X$
on
![]() $X_{\textrm {\'et}}$
, together with a morphism
$X_{\textrm {\'et}}$
, together with a morphism
![]() $\alpha _X: M_X \to \mathcal {O}_X$
such that
$\alpha _X: M_X \to \mathcal {O}_X$
such that
![]() $\alpha _X^{-1}(\mathcal {O}_X^{\times }) \simeq \mathcal {O}_X^{\times }$
. A scheme endowed with a log structure is said to be a logarithmic (log) scheme.
$\alpha _X^{-1}(\mathcal {O}_X^{\times }) \simeq \mathcal {O}_X^{\times }$
. A scheme endowed with a log structure is said to be a logarithmic (log) scheme.
A morphism of log schemes is a morphism
![]() $f : X \to Y$
of the underlying schemes, together with a morphism
$f : X \to Y$
of the underlying schemes, together with a morphism
![]() $f^{-1}M_Y \to M_X$
such that the diagram
$f^{-1}M_Y \to M_X$
such that the diagram

commutes.
2.1.2. Charts
If
![]() $\underline {P}$
is the constant sheaf associated with a monoid P, and if we are given a morphism of sheaves
$\underline {P}$
is the constant sheaf associated with a monoid P, and if we are given a morphism of sheaves
![]() $\underline {P} \to \mathcal {O}_X$
, it induces a unique log structure on X [Reference Ogus13, Prop. 1.1.5]. If
$\underline {P} \to \mathcal {O}_X$
, it induces a unique log structure on X [Reference Ogus13, Prop. 1.1.5]. If
![]() $(X,M_X)$
is a log scheme, it is said to have a chart on P if the log structure induced by P is isomorphic to
$(X,M_X)$
is a log scheme, it is said to have a chart on P if the log structure induced by P is isomorphic to
![]() $M_X$
. All the log schemes in this paper are supposed to admit charts étale locally. Furthermore, if P is fine (finitely generated and integral, i.e.,
$M_X$
. All the log schemes in this paper are supposed to admit charts étale locally. Furthermore, if P is fine (finitely generated and integral, i.e.,
![]() $P \hookrightarrow P^{gp}$
) and saturated (i.e., if
$P \hookrightarrow P^{gp}$
) and saturated (i.e., if
![]() $a \in P^{gp}$
such that
$a \in P^{gp}$
such that
![]() $a^n \in P$
for some nonzero integer n, then
$a^n \in P$
for some nonzero integer n, then
![]() $a \in P$
), X is said to be a fine and saturated log scheme; we refer to [Reference Ogus13] for further details.
$a \in P$
), X is said to be a fine and saturated log scheme; we refer to [Reference Ogus13] for further details.
2.1.3. Inverse image log structure and strict morphisms
If Y is a log scheme with underlying scheme
![]() $\underline {Y}$
, and
$\underline {Y}$
, and
![]() $f: X \to \underline {Y}$
is a morphism of schemes, then the composition
$f: X \to \underline {Y}$
is a morphism of schemes, then the composition
![]() $f^{-1}M_Y \xrightarrow {f^{-1}\alpha _Y} f^{-1}\mathcal {O}_Y \to \mathcal {O}_X$
is a prelog structure on X, and induces the inverse image log structure on X that we denote by
$f^{-1}M_Y \xrightarrow {f^{-1}\alpha _Y} f^{-1}\mathcal {O}_Y \to \mathcal {O}_X$
is a prelog structure on X, and induces the inverse image log structure on X that we denote by
![]() $f^{*}M_Y$
.
$f^{*}M_Y$
.
If
![]() $f: X \to Y$
is a morphism of log schemes, the map
$f: X \to Y$
is a morphism of log schemes, the map
![]() $f^{-1}M_Y \to M_X$
factors canonically through
$f^{-1}M_Y \to M_X$
factors canonically through
![]() $f^{*}M_Y \to M_X$
.
$f^{*}M_Y \to M_X$
.
The morphism of log schemes
![]() $f:X \to Y$
is said to be strict if the induced map
$f:X \to Y$
is said to be strict if the induced map
![]() $f^*M_Y \to M_X$
is an isomorphism.
$f^*M_Y \to M_X$
is an isomorphism.
2.1.4. Direct image log structure
If
![]() $f : X \to Y$
is a morphism of schemes and
$f : X \to Y$
is a morphism of schemes and
![]() $\alpha _X : M_X \to \mathcal {O}_X$
is a log structure on X, then the natural map
$\alpha _X : M_X \to \mathcal {O}_X$
is a log structure on X, then the natural map
![]() $\beta $
in the diagram below
$\beta $
in the diagram below

is a log structure on Y, called the direct image log structure induced by
![]() $\alpha _X$
. We denote it by
$\alpha _X$
. We denote it by
![]() $f^{log}_* \alpha _X: f^{log}_* M_X \to \mathcal {O}_Y$
.
$f^{log}_* \alpha _X: f^{log}_* M_X \to \mathcal {O}_Y$
.
Example 2.1.
-
1. Let X be a scheme.
 $M_X:=\mathcal {O}_X^{\times }$
defines a fine and saturated log structure on X called the trivial log structure. X has a chart on the monoid
$M_X:=\mathcal {O}_X^{\times }$
defines a fine and saturated log structure on X called the trivial log structure. X has a chart on the monoid
 $\{1\}$
. If X is a log scheme, the largest Zariski open subset of X (possibly empty) on which the log structure is trivial is called the open of triviality of X.
$\{1\}$
. If X is a log scheme, the largest Zariski open subset of X (possibly empty) on which the log structure is trivial is called the open of triviality of X. -
2. Let X be a regular scheme, and let
 $j: U \hookrightarrow X$
be a dense open subset whose complementary is a normal crossing divisor D on X. Then the sheaf defines the divisorial log structure on X.
$j: U \hookrightarrow X$
be a dense open subset whose complementary is a normal crossing divisor D on X. Then the sheaf defines the divisorial log structure on X. $$\begin{align*}M_X(V):= \{s \in \mathcal{O}_X(V) | s_{|V \cap U} \in \mathcal{O}_{V \cap U}(V \cap U)^{\times}\} \hookrightarrow \mathcal{O}_X(V)\end{align*}$$
$$\begin{align*}M_X(V):= \{s \in \mathcal{O}_X(V) | s_{|V \cap U} \in \mathcal{O}_{V \cap U}(V \cap U)^{\times}\} \hookrightarrow \mathcal{O}_X(V)\end{align*}$$
It is the same as the direct image log structure on X of the trivial log structure on U, that is,
 $j^{log}_*\mathcal {O}_U^{\times }$
(cf. [Reference Kato8, §1.5]). It is a fine and saturated log structure on X.
$j^{log}_*\mathcal {O}_U^{\times }$
(cf. [Reference Kato8, §1.5]). It is a fine and saturated log structure on X.Note that U is the open of triviality of the divisorial log structure on X. In particular,
 $\operatorname {\mathrm {Spec}}(R)$
can be seen as a fine and saturated log scheme with the log structure induced by
$\operatorname {\mathrm {Spec}}(R)$
can be seen as a fine and saturated log scheme with the log structure induced by
 $\operatorname {\mathrm {Spec}}(k)$
seen as a divisor.
$\operatorname {\mathrm {Spec}}(k)$
seen as a divisor.
 $\operatorname {\mathrm {Spec}}(R)$
has a chart on
$\operatorname {\mathrm {Spec}}(R)$
has a chart on
 $\mathbb N$
given by
$\mathbb N$
given by
 $\mathbb N \to R; 1 \mapsto \pi $
, where
$\mathbb N \to R; 1 \mapsto \pi $
, where
 $\pi $
is the uniformizer of R. More generally, if
$\pi $
is the uniformizer of R. More generally, if
 ${X}$
is a flat R-scheme such that its special fiber is a normal crossing divisor, then it can be seen as a fine and saturated log scheme with the log structure induced by its special fiber. The generic fiber
${X}$
is a flat R-scheme such that its special fiber is a normal crossing divisor, then it can be seen as a fine and saturated log scheme with the log structure induced by its special fiber. The generic fiber
 ${X}_K$
is the open of triviality of the log structure. Furthermore, it has (étale) locally a chart on
${X}_K$
is the open of triviality of the log structure. Furthermore, it has (étale) locally a chart on
 $\mathbb {N}^r$
.
$\mathbb {N}^r$
. -
3. If S is a fine and saturated log scheme, we say that
 $ {X} \to S$
is a log curve if it is a proper, integral (cf. [Reference Kato7, Def. 2.3]), vertical,Footnote
1
log smooth morphism of (fine and saturated) log schemes with connected and reduced geometric fibers of pure dimension
$ {X} \to S$
is a log curve if it is a proper, integral (cf. [Reference Kato7, Def. 2.3]), vertical,Footnote
1
log smooth morphism of (fine and saturated) log schemes with connected and reduced geometric fibers of pure dimension
 $1$
. Then, according to [Reference Kato6], the underlying scheme of
$1$
. Then, according to [Reference Kato6], the underlying scheme of
 ${X}$
is a flat family of nodal curves over S and one has an explicit description of the log structure on the geometric points of
${X}$
is a flat family of nodal curves over S and one has an explicit description of the log structure on the geometric points of
 ${X}$
lying above geometric points of S. This is a fine and saturated log structure on X. Conversely, if S is the spectrum of a DVR R and
${X}$
lying above geometric points of S. This is a fine and saturated log structure on X. Conversely, if S is the spectrum of a DVR R and
 $K=\mathrm {Frac}(R)$
, if
$K=\mathrm {Frac}(R)$
, if
 $C/K$
is a semistable curve with
$C/K$
is a semistable curve with
 $\mathcal {C}$
some regular model over S, there exist canonical log structures on
$\mathcal {C}$
some regular model over S, there exist canonical log structures on
 $\mathcal {C}$
and S making
$\mathcal {C}$
and S making
 $\mathcal {C} \to S$
a log curve (cf. [Reference Olsson14, §3]). Furthermore, if S is endowed with its divisorial log structure, and if the special fiber of
$\mathcal {C} \to S$
a log curve (cf. [Reference Olsson14, §3]). Furthermore, if S is endowed with its divisorial log structure, and if the special fiber of
 $\mathcal {C}/S$
is a normal crossing divisor, tho so-mentioned canonical log structure on
$\mathcal {C}/S$
is a normal crossing divisor, tho so-mentioned canonical log structure on
 $\mathcal {C}$
agrees with the divisorial one (cf. [Reference Molcho and Wise12, §2 of proof of Lemma 2.2.5.1 and Theorem 2.4.1.3]).
$\mathcal {C}$
agrees with the divisorial one (cf. [Reference Molcho and Wise12, §2 of proof of Lemma 2.2.5.1 and Theorem 2.4.1.3]).
We consider here the category of fine and saturated log schemes, endowed with the Kummer log flat topology (we sometimes write klf to refer to this topology for simplicity). We refer to [Reference Kato8] or [Reference Gillibert4, §2.2] for the definition of this Grothendieck topology. A torsor in this category, defined with respect to the klf topology, is called a logarithmic torsor (or a log torsor). The structural group of the torsor is always assumed to be endowed with the strict log structure (the inverse log structure of that of the base). Moreover, a Kummer log flat cover of a scheme endowed with the trivial log structure is just a cover for the fppf topology. So, in this paper, the category of schemes is endowed with the fppf topology.
Example 2.2 [Reference Kato9, §1; 1.9.3]
Let A be a discrete valuation ring with uniformizer
![]() $\pi $
. Assume that it contains a primitive nth root of unity and that
$\pi $
. Assume that it contains a primitive nth root of unity and that
![]() $n \in \mathbb N$
is invertible in A. We set
$n \in \mathbb N$
is invertible in A. We set
![]() $B:=A[\sqrt [n]{\pi }]$
,
$B:=A[\sqrt [n]{\pi }]$
,
![]() $X:=\operatorname {\mathrm {Spec}}(A)$
and
$X:=\operatorname {\mathrm {Spec}}(A)$
and
![]() $Y:=\operatorname {\mathrm {Spec}}(B)$
. We endow both these schemes with the divisorial log structure, making them into fine saturated log schemes. Let
$Y:=\operatorname {\mathrm {Spec}}(B)$
. We endow both these schemes with the divisorial log structure, making them into fine saturated log schemes. Let
![]() $G:=\mathrm {Aut}_A(B)=\mu _n\simeq \mathbb Z/n\mathbb Z$
. Then
$G:=\mathrm {Aut}_A(B)=\mu _n\simeq \mathbb Z/n\mathbb Z$
. Then
![]() $Y \to X$
is not an fppf G-torsor (because it is totally ramified while G is unramified), but it is a klf (more precisely, Kummer log étale) torsor.
$Y \to X$
is not an fppf G-torsor (because it is totally ramified while G is unramified), but it is a klf (more precisely, Kummer log étale) torsor.
2.2. Extension of torsors under a finite flat group scheme
We recall briefly in this section the main results of [Reference Mehidi11] on the problem of extending torsors under finite flat group schemes. From now on,
![]() $\operatorname {\mathrm {Spec}}(R)$
is endowed with the divisorial log structure. Let
$\operatorname {\mathrm {Spec}}(R)$
is endowed with the divisorial log structure. Let
![]() $(fs/R)_{klf}$
denote the category of fine and saturated log schemes over R endowed with the Kummer log flat topology, and let
$(fs/R)_{klf}$
denote the category of fine and saturated log schemes over R endowed with the Kummer log flat topology, and let
![]() $(Sch/R)_{fppf}$
be the category of schemes over R endowed with the fppf topology. The latter can be viewed as a full subcategory of
$(Sch/R)_{fppf}$
be the category of schemes over R endowed with the fppf topology. The latter can be viewed as a full subcategory of
![]() $(fs/R)_{klf}$
by endowing an R-scheme with the inverse log structure of that of
$(fs/R)_{klf}$
by endowing an R-scheme with the inverse log structure of that of
![]() $\operatorname {\mathrm {Spec}}(R)$
. We recall the following definitions:
$\operatorname {\mathrm {Spec}}(R)$
. We recall the following definitions:
Definition 2.3.
-
1. We define the following functor:
which is a sheaf in the klf site [Reference Kato8, Th. 3.2]. Note that generically, it is isomorphic to $$ \begin{align*} \mathbb{G}_{m,log,R}: (fs/R)_{klf} &\to (Ab)\\ T & \mapsto \Gamma(T,M_T^{gp}), \end{align*} $$
$$ \begin{align*} \mathbb{G}_{m,log,R}: (fs/R)_{klf} &\to (Ab)\\ T & \mapsto \Gamma(T,M_T^{gp}), \end{align*} $$
 $\mathbb {G}_{m,K}$
.
$\mathbb {G}_{m,K}$
.
-
2. Let C be a smooth projective K-curve with an R-regular model
 $\mathcal {C}$
endowed with the divisorial log structure. Using the embedding
$\mathcal {C}$
endowed with the divisorial log structure. Using the embedding
 $(Sch/R)_{fppf} \hookrightarrow (fs/R)_{klf}$
, consider the following functor: The log Picard functor, denoted by
$(Sch/R)_{fppf} \hookrightarrow (fs/R)_{klf}$
, consider the following functor: The log Picard functor, denoted by $$ \begin{align*} (Sch/R)_{fppf} &\to (Sets)\\ T & \mapsto \{\mathbb{G}_{m,log,\mathcal{C}}-log~torsors~on~\mathcal{C}_{T} \}. \end{align*} $$
$$ \begin{align*} (Sch/R)_{fppf} &\to (Sets)\\ T & \mapsto \{\mathbb{G}_{m,log,\mathcal{C}}-log~torsors~on~\mathcal{C}_{T} \}. \end{align*} $$
 $\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
, is defined to be the fppf sheaffification on
$\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
, is defined to be the fppf sheaffification on
 $(Sch/R)_{fppf}$
of the previous functor. Furthermore, it is clear that its generic fiber is
$(Sch/R)_{fppf}$
of the previous functor. Furthermore, it is clear that its generic fiber is
 $\operatorname {\mathrm {Pic}}_{C/K}$
, the usual relative Picard functor of
$\operatorname {\mathrm {Pic}}_{C/K}$
, the usual relative Picard functor of
 $C/K$
.
$C/K$
.
Theorem 2.4 [Reference Mehidi11, Rem. 1.11]
Let C be a smooth projective and geometrically connected curve over K, endowed with a K-point Q, and let J denote its Jacobian variety. Let
![]() $\mathcal {C}$
be an R-regular model of C such that its special fiber is a normal crossing divisor. Endow
$\mathcal {C}$
be an R-regular model of C such that its special fiber is a normal crossing divisor. Endow
![]() $\mathcal {C}$
with the divisorial log structure, and let
$\mathcal {C}$
with the divisorial log structure, and let
![]() $\mathcal {Q}$
be the R-section that extends Q over
$\mathcal {Q}$
be the R-section that extends Q over
![]() $\mathcal {C}$
. Let G be a finite commutative K-group scheme with finite flat R-model
$\mathcal {C}$
. Let G be a finite commutative K-group scheme with finite flat R-model
![]() $\mathcal {G}$
, and let
$\mathcal {G}$
, and let
![]() $\mathcal {G}^D$
denote its Cartier dual. We have a canonical isomorphism:
$\mathcal {G}^D$
denote its Cartier dual. We have a canonical isomorphism:
where
![]() $H^1_{klf}(\mathcal {C},\mathcal {Q},\mathcal {G})$
denotes the cohomology group that classifies logarithmic
$H^1_{klf}(\mathcal {C},\mathcal {Q},\mathcal {G})$
denotes the cohomology group that classifies logarithmic
![]() $\mathcal {G}$
-torsors over
$\mathcal {G}$
-torsors over
![]() $\mathcal {C}$
, pointed relatively to
$\mathcal {C}$
, pointed relatively to
![]() $\mathcal {Q}$
. In particular, a pointed fppf G-torsor (relatively to Q) over C extends into a pointed log
$\mathcal {Q}$
. In particular, a pointed fppf G-torsor (relatively to Q) over C extends into a pointed log
![]() $\mathcal {G}$
-torsor (relatively to
$\mathcal {G}$
-torsor (relatively to
![]() $\mathcal {Q}$
) over
$\mathcal {Q}$
) over
![]() $\mathcal {C}$
if and only if the associated K-morphism
$\mathcal {C}$
if and only if the associated K-morphism
![]() $G^D \to J$
(cf. (⋆)) extends into an R-morphism
$G^D \to J$
(cf. (⋆)) extends into an R-morphism
![]() $\mathcal {G}^D \to \operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
.
$\mathcal {G}^D \to \operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
.
Proposition 2.5 [Reference Mehidi11, Props. 1.12 and 1.18]
With the assumptions of the previous theorem, if
![]() $\mathcal {J}$
is the Néron model of J over R, then the closed immersion
$\mathcal {J}$
is the Néron model of J over R, then the closed immersion
![]() $J \hookrightarrow \operatorname {\mathrm {Pic}}_{C/K}$
extends uniquely into an R-morphism
$J \hookrightarrow \operatorname {\mathrm {Pic}}_{C/K}$
extends uniquely into an R-morphism
![]() $\mathcal {J} \to \operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
. In particular, if the associated K-morphism
$\mathcal {J} \to \operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
. In particular, if the associated K-morphism
![]() $G^D \to J$
of the generic torsor extends into an R-morphism
$G^D \to J$
of the generic torsor extends into an R-morphism
![]() $\mathcal {G}^D \to \mathcal {J}$
, the torsor extends into a
$\mathcal {G}^D \to \mathcal {J}$
, the torsor extends into a
![]() $\mathcal {G}$
-log torsor over
$\mathcal {G}$
-log torsor over
![]() $\mathcal {C}$
. Moreover, if
$\mathcal {C}$
. Moreover, if
![]() $\mathcal {J}^0$
denotes the identity component of
$\mathcal {J}^0$
denotes the identity component of
![]() $\mathcal {J}$
, the extended log torsor is fppf if and only if
$\mathcal {J}$
, the extended log torsor is fppf if and only if
![]() $\mathcal {G}^D \to \mathcal {J}$
factors through
$\mathcal {G}^D \to \mathcal {J}$
factors through
![]() $\mathcal {J}^0$
.
$\mathcal {J}^0$
.
3. Part I: Case of semistable curves
3.1. The Log Picard functor
Recently, the Picard log functor has been defined in a more general frame. Let S be a log regular scheme, and let
![]() $U \subseteq S$
be the open of triviality of the log structure on S (which is nonempty and even dense in S by log regularity). Let
$U \subseteq S$
be the open of triviality of the log structure on S (which is nonempty and even dense in S by log regularity). Let
![]() ${X} \to S$
be a logarithmic curve (hence smooth over U). In [Reference Molcho and Wise12], following the ideas of Illusie and Kato, the authors constructed the analogue of the Picard functor in the logarithmic setting: the logarithmic Picard group that they denoted by
${X} \to S$
be a logarithmic curve (hence smooth over U). In [Reference Molcho and Wise12], following the ideas of Illusie and Kato, the authors constructed the analogue of the Picard functor in the logarithmic setting: the logarithmic Picard group that they denoted by
![]() $\mathrm {LogPic}_{{X}/S}$
. It is the sheaf of isomorphism classes of the stack which parameterizes the logarithmic line bundles, that is, torsors under the group scheme
$\mathrm {LogPic}_{{X}/S}$
. It is the sheaf of isomorphism classes of the stack which parameterizes the logarithmic line bundles, that is, torsors under the group scheme
![]() $\mathbb {G}_{m,log,S}$
, which verify a certain condition called the condition of bounded monodromy.
$\mathbb {G}_{m,log,S}$
, which verify a certain condition called the condition of bounded monodromy.
Naturally, the logarithmic Picard group coincides with the ordinary Picard group over
![]() ${X}_U$
, where the log structure is trivial. Furthermore, logarithmic line bundles have a natural notion of (total) degree extending the notion of degree of classical line bundles (cf. [Reference Molcho and Wise12, §4.5]).
${X}_U$
, where the log structure is trivial. Furthermore, logarithmic line bundles have a natural notion of (total) degree extending the notion of degree of classical line bundles (cf. [Reference Molcho and Wise12, §4.5]).
Using this notion of degree, it is defined in [Reference Holmes, Molcho, Orecchia and Poiret5, De. 3.47]
![]() $\mathrm {LogPic}^0_{{X}/S}$
, the subsheaf of
$\mathrm {LogPic}^0_{{X}/S}$
, the subsheaf of
![]() $\mathrm {LogPic_{{X}/S}}$
consisting of log line bundles of total degree zero, which they called the logarithmic Jacobian. In fact, this provides the best possible extension of the Jacobian
$\mathrm {LogPic_{{X}/S}}$
consisting of log line bundles of total degree zero, which they called the logarithmic Jacobian. In fact, this provides the best possible extension of the Jacobian
![]() $\operatorname {\mathrm {Pic}}^0_{{X}_U/U}$
.
$\operatorname {\mathrm {Pic}}^0_{{X}_U/U}$
.
Furthermore, one can restrict the functor
![]() $\mathrm {LogPic}^0_{{X}/S}$
to the category of schemes via the embedding
$\mathrm {LogPic}^0_{{X}/S}$
to the category of schemes via the embedding
![]() $(Sch)_{fppf} \hookrightarrow (fs/S)_{klf}$
, and the resulting functor is called the strict logarithmic Jacobian and denoted by
$(Sch)_{fppf} \hookrightarrow (fs/S)_{klf}$
, and the resulting functor is called the strict logarithmic Jacobian and denoted by
![]() $\mathrm {sLogPic^0}_{{X}/S}$
(cf. [Reference Holmes, Molcho, Orecchia and Poiret5, Def. 4.5]).
$\mathrm {sLogPic^0}_{{X}/S}$
(cf. [Reference Holmes, Molcho, Orecchia and Poiret5, Def. 4.5]).
Theorem 3.1 [Reference Holmes, Molcho, Orecchia and Poiret5, Cor. 6.13]
![]() $\mathrm {sLogPic}^0_{{X}/S}$
is the Néron model of
$\mathrm {sLogPic}^0_{{X}/S}$
is the Néron model of
![]() $~\operatorname {\mathrm {Pic}}^0_{{X}_U/U}$
.
$~\operatorname {\mathrm {Pic}}^0_{{X}_U/U}$
.
Remark 3.2. The condition of bounded monodromy is essential to get a log Picard group of
![]() $X/S$
that is well behaved in families. For the purposes of this paper, we do not need to recall its definition in the general setting; we will simply recall it in the case where the base S is the spectrum of a discrete valuation ring endowed with the divisorial log structure. We will see that in this case, this condition is automatically satisfied.
$X/S$
that is well behaved in families. For the purposes of this paper, we do not need to recall its definition in the general setting; we will simply recall it in the case where the base S is the spectrum of a discrete valuation ring endowed with the divisorial log structure. We will see that in this case, this condition is automatically satisfied.
So we take S to be
![]() $\operatorname {\mathrm {Spec}}(R)$
endowed with the divisorial log structure. Let X denote an R-log curve, and let
$\operatorname {\mathrm {Spec}}(R)$
endowed with the divisorial log structure. Let X denote an R-log curve, and let
![]() $s=\operatorname {\mathrm {Spec}}(\bar {k})$
denote the geometric closed point of
$s=\operatorname {\mathrm {Spec}}(\bar {k})$
denote the geometric closed point of
![]() $\operatorname {\mathrm {Spec}}(R)$
. If
$\operatorname {\mathrm {Spec}}(R)$
. If
![]() $\Gamma $
denotes the dual graph (which is assumed to be oriented) of
$\Gamma $
denotes the dual graph (which is assumed to be oriented) of
![]() $X_{s}$
and if
$X_{s}$
and if
![]() $M_R$
denotes the divisorial log structure over the base
$M_R$
denotes the divisorial log structure over the base
![]() $\operatorname {\mathrm {Spec}}(R)$
, one can define on
$\operatorname {\mathrm {Spec}}(R)$
, one can define on
![]() $\Gamma $
a length map
$\Gamma $
a length map
![]() $l: \Gamma \to \overline {M_R}_{,s}$
, where
$l: \Gamma \to \overline {M_R}_{,s}$
, where
![]() $\overline {M_R}:=M_R/\mathcal {O}_R^*$
. Since
$\overline {M_R}:=M_R/\mathcal {O}_R^*$
. Since
![]() $M_R=\mathcal {O}_R \cap \mathcal {O}_K^*$
, one finds that
$M_R=\mathcal {O}_R \cap \mathcal {O}_K^*$
, one finds that
![]() $\overline {M_R}_{,s}\simeq \mathbb {N}$
.
$\overline {M_R}_{,s}\simeq \mathbb {N}$
.
The data
![]() $\mathcal {X}=(\Gamma , l: \Gamma \to \mathbb N)$
are called the tropical curve associated with
$\mathcal {X}=(\Gamma , l: \Gamma \to \mathbb N)$
are called the tropical curve associated with
![]() $X_{s}$
(cf. [Reference Molcho and Wise12, §2.3]). In addition, on can define a topology on tropical curves (cf. [Reference Molcho and Wise12, §3]) which allows to do homology on them. In particular, the length map l can be extended to
$X_{s}$
(cf. [Reference Molcho and Wise12, §2.3]). In addition, on can define a topology on tropical curves (cf. [Reference Molcho and Wise12, §3]) which allows to do homology on them. In particular, the length map l can be extended to
![]() $H_1(\mathcal {X})$
.
$H_1(\mathcal {X})$
.
To any log line bundle over X is associated a class of morphisms
![]() $H_1(\mathcal {X}) \to \overline {M_R}_{,s}^{gp}=\mathbb N^{gp}=\mathbb Z$
, called the monodromy class (cf. [Reference Molcho and Wise12, §§3.5 and 4.1]). A logarithmic line bundle is said to have bounded monodromy if for any
$H_1(\mathcal {X}) \to \overline {M_R}_{,s}^{gp}=\mathbb N^{gp}=\mathbb Z$
, called the monodromy class (cf. [Reference Molcho and Wise12, §§3.5 and 4.1]). A logarithmic line bundle is said to have bounded monodromy if for any
![]() $\gamma \in H_1(\mathcal {X}), \exists n \in \mathbb N$
such that
$\gamma \in H_1(\mathcal {X}), \exists n \in \mathbb N$
such that
![]() $-nl(\gamma ) \leq \alpha (\gamma ) \leq nl(\gamma )$
, where
$-nl(\gamma ) \leq \alpha (\gamma ) \leq nl(\gamma )$
, where
![]() $\alpha : H_1(\mathcal {X}) \to \mathbb Z$
is some representative in the monodromy class of the line bundle (this condition does not depend on the choice of a representative).
$\alpha : H_1(\mathcal {X}) \to \mathbb Z$
is some representative in the monodromy class of the line bundle (this condition does not depend on the choice of a representative).
![]() $\overline {M_R}_{,s}\simeq \mathbb {N}$
being archimedean, it is clear that the monodromy condition is automatically satisfied in this setting.
$\overline {M_R}_{,s}\simeq \mathbb {N}$
being archimedean, it is clear that the monodromy condition is automatically satisfied in this setting.
Therefore, in the case where S is the spectrum of a discrete valuation ring endowed with its divisorial log structure, the condition of bounded monodromy is automatically satisfied, which means that log line bundles consist of all the
![]() $\mathbb {G}_{m,log,S}$
-torsors. In particular,
$\mathbb {G}_{m,log,S}$
-torsors. In particular,
![]() $\mathrm {sLogPic_{X/S}}$
coincides with the log Picard functor we recalled in §2.2.
$\mathrm {sLogPic_{X/S}}$
coincides with the log Picard functor we recalled in §2.2.
Proposition 3.3. Let C be a smooth projective semistable and geometrically connected curve endowed with a K-point. Let
![]() $\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure. Let
$\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure. Let
![]() $\mathcal {G}$
be a finite flat R-group scheme. Then any R-morphism
$\mathcal {G}$
be a finite flat R-group scheme. Then any R-morphism
![]() $\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through
$\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through
![]() $\mathrm {sLogPic}^0_{\mathcal {C}/R}$
.
$\mathrm {sLogPic}^0_{\mathcal {C}/R}$
.
Proof. According to the previous remark,
![]() $\mathrm {sLogPic}^0_{\mathcal {C}/R}$
is the subsheaf of
$\mathrm {sLogPic}^0_{\mathcal {C}/R}$
is the subsheaf of
![]() $\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
of (total) degree zero log line bundles. On the other hand, since
$\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
of (total) degree zero log line bundles. On the other hand, since
![]() $\mathcal {G}$
is of torsion, the morphism
$\mathcal {G}$
is of torsion, the morphism
![]() $\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through the torsion of
$\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through the torsion of
![]() $\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
. Now, given the (total) degree map
$\operatorname {\mathrm {Pic}}^{log}_{\mathcal {C}/R}$
. Now, given the (total) degree map
![]() $\mathrm {Pic}^{log}_{\mathcal {C}/R} \xrightarrow {\mathrm {deg}} \mathbb {Z}$
and the fact that
$\mathrm {Pic}^{log}_{\mathcal {C}/R} \xrightarrow {\mathrm {deg}} \mathbb {Z}$
and the fact that
![]() $\mathbb Z$
has no torsion, we deduce that torsion log line bundles have (total) degree zero. In addition,
$\mathbb Z$
has no torsion, we deduce that torsion log line bundles have (total) degree zero. In addition,
![]() $\mathcal {G} \to \operatorname {\mathrm {Spec}}(R)$
being strict, we conclude that
$\mathcal {G} \to \operatorname {\mathrm {Spec}}(R)$
being strict, we conclude that
![]() $\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through
$\mathcal {G} \to \mathrm {Pic}^{log}_{\mathcal {C}/R}$
factors through
![]() $\mathrm {sLogPic}^0_{\mathcal {C}/R}$
.
$\mathrm {sLogPic}^0_{\mathcal {C}/R}$
.
Corollary 3.4. Let C be a smooth projective semistable and geometrically connected curve endowed with a K-point. Let
![]() $\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure (cf. example 2.1(3)). Let G be a finite commutative K-group scheme, and let
$\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure (cf. example 2.1(3)). Let G be a finite commutative K-group scheme, and let
![]() $\mathcal {G}$
be a finite flat R-model of G. Then a pointed fppf G-torsor extends into a pointed
$\mathcal {G}$
be a finite flat R-model of G. Then a pointed fppf G-torsor extends into a pointed
![]() $\mathcal {G}$
-log torsor over
$\mathcal {G}$
-log torsor over
![]() $\mathcal {C}$
if and only if the K-morphism
$\mathcal {C}$
if and only if the K-morphism
![]() $G^D \to J$
associated with the generic torsor (cf. (⋆)) extends into an R-morphism
$G^D \to J$
associated with the generic torsor (cf. (⋆)) extends into an R-morphism
![]() $\mathcal {G}^D \to \mathcal {J}$
.
$\mathcal {G}^D \to \mathcal {J}$
.
3.2. On the existence of a finite flat model of the group scheme
We assume in this section that k is algebraically closed. Let C be a semistable smooth projective and geometrically connected K-curve with Jacobian variety J. Assume that G is a finite commutative subgroup scheme of J. In particular, the morphism
![]() $G \hookrightarrow J$
factors through
$G \hookrightarrow J$
factors through
![]() $J[r]$
, where r is the order of G. If
$J[r]$
, where r is the order of G. If
![]() $\mathcal {J}$
is the Néron model of J, we let
$\mathcal {J}$
is the Néron model of J, we let
![]() $\overline {G}$
be the schematic closure of G inside
$\overline {G}$
be the schematic closure of G inside
![]() $\mathcal {J}[r]$
. Since C is semistable,
$\mathcal {J}[r]$
. Since C is semistable,
![]() $\mathcal {J}[r]$
is flat and quasi-finite (cf. [Reference Bosch, Lütkebohmert and Raynaud3, §7.3, Lem. 2]).
$\mathcal {J}[r]$
is flat and quasi-finite (cf. [Reference Bosch, Lütkebohmert and Raynaud3, §7.3, Lem. 2]).
In a previous paper (cf. [Reference Mehidi11, §3]), we found a necessary and sufficient condition for
![]() $\mathcal {J}[r]$
to be finite and flat,Footnote
2
hence for G to admit a finite flat R-model, namely
$\mathcal {J}[r]$
to be finite and flat,Footnote
2
hence for G to admit a finite flat R-model, namely
![]() $\overline {G}$
.
$\overline {G}$
.
Question. If
![]() $\mathcal {J}[r]$
is not assumed to be finite flat anymore, can we still find a necessary and sufficient condition for the schematic closure
$\mathcal {J}[r]$
is not assumed to be finite flat anymore, can we still find a necessary and sufficient condition for the schematic closure
![]() $\overline {G}$
of G to be finite and flat?
$\overline {G}$
of G to be finite and flat?
For the rest of the section, we assume that R is Henselian. Since
![]() $\mathcal {J}[r]$
is quasi-finite and R Henselian, according to [Reference Mazur10, Lem. 1.1], we have an exact sequence
$\mathcal {J}[r]$
is quasi-finite and R Henselian, according to [Reference Mazur10, Lem. 1.1], we have an exact sequence
where
![]() $\mathcal {FJ}[r]$
is a finite flat group scheme over R and
$\mathcal {FJ}[r]$
is a finite flat group scheme over R and
![]() $\mathcal {EJ}[r]$
is a étale group scheme over R, with trivial special fiber. In particular, it follows from [1, §IX, Lem. 2.2.3] that
$\mathcal {EJ}[r]$
is a étale group scheme over R, with trivial special fiber. In particular, it follows from [1, §IX, Lem. 2.2.3] that
![]() $\mathcal {FJ}[r]$
is the largest finite subgroup scheme in
$\mathcal {FJ}[r]$
is the largest finite subgroup scheme in
![]() $\mathcal {J}[r]$
.
$\mathcal {J}[r]$
.
The schematic closure
![]() $\overline {G}$
of G in
$\overline {G}$
of G in
![]() $\mathcal {J}[r]$
is flat and quasi-finite. Hence, we have as previously an exact sequence
$\mathcal {J}[r]$
is flat and quasi-finite. Hence, we have as previously an exact sequence
where
![]() $\mathcal {F}$
is a finite flat group scheme over R and
$\mathcal {F}$
is a finite flat group scheme over R and
![]() $\mathcal {E}$
is a étale group scheme over R, with trivial special fiber. We would like to find a necessary and sufficient condition for
$\mathcal {E}$
is a étale group scheme over R, with trivial special fiber. We would like to find a necessary and sufficient condition for
![]() $\overline {G}$
to be finite.
$\overline {G}$
to be finite.
We denote by
![]() $\mathcal {FJ}[r]_K$
the generic fiber of
$\mathcal {FJ}[r]_K$
the generic fiber of
![]() $\mathcal {FJ}[r]$
.
$\mathcal {FJ}[r]$
.
Lemma 3.5.
![]() $\overline {G}$
is finite if and only if
$\overline {G}$
is finite if and only if
![]() $G \to J[r]$
factors through
$G \to J[r]$
factors through
![]() $\mathcal {FJ}[r]_K$
.
$\mathcal {FJ}[r]_K$
.
Proof. If
![]() $\overline {G}$
is finite, since
$\overline {G}$
is finite, since
![]() $\mathcal {FJ}[r]$
is the largest finite subgroup scheme inside
$\mathcal {FJ}[r]$
is the largest finite subgroup scheme inside
![]() $\mathcal {J}[r]$
, then
$\mathcal {J}[r]$
, then
![]() $\overline {G} \to \mathcal {J}[r]$
factors through
$\overline {G} \to \mathcal {J}[r]$
factors through
![]() $\mathcal {FJ}[r]$
; hence,
$\mathcal {FJ}[r]$
; hence,
![]() $G \to J[r]$
factors through
$G \to J[r]$
factors through
![]() $\mathcal {FJ}[r]_K$
.
$\mathcal {FJ}[r]_K$
.
On the other hand, if
![]() ${G} \to {J}[r]$
factors through
${G} \to {J}[r]$
factors through
![]() $\mathcal {FJ}[r]_K$
, since
$\mathcal {FJ}[r]_K$
, since
![]() $\mathcal {FJ}[r]$
is closed inside
$\mathcal {FJ}[r]$
is closed inside
![]() $\mathcal {J}[r]$
(it is a kernel),
$\mathcal {J}[r]$
(it is a kernel),
![]() $\overline {G}$
is the schematic closure of G in
$\overline {G}$
is the schematic closure of G in
![]() $\mathcal {FJ}[r]$
; hence, it is finite (closed immersions are finite and the composition of two finite morphisms is finite).
$\mathcal {FJ}[r]$
; hence, it is finite (closed immersions are finite and the composition of two finite morphisms is finite).
Corollary 3.6. Let C be a semistable smooth projective and geometrically connected curve with a K-point, let
![]() $\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure, and let J be the Jacobian of C and
$\mathcal {C}$
be an R-regular model of C with normal crossing special fiber and endowed with the divisorial log structure, and let J be the Jacobian of C and
![]() $\mathcal {J}$
its Néron model. Let G be a finite subgroup scheme of J. Then, the corresponding fppf pointed
$\mathcal {J}$
its Néron model. Let G be a finite subgroup scheme of J. Then, the corresponding fppf pointed
![]() $G^D$
-torsor
$G^D$
-torsor
![]() $Y \to C$
(cf. (⋆)) extends into a log torsor over
$Y \to C$
(cf. (⋆)) extends into a log torsor over
![]() $\mathcal {C}$
under a finite flat group scheme if and only if G is a subgroup of
$\mathcal {C}$
under a finite flat group scheme if and only if G is a subgroup of
![]() $\mathcal {FJ}[r]_K$
, with r the order of G.
$\mathcal {FJ}[r]_K$
, with r the order of G.
Proof. If
![]() $G \hookrightarrow J[r]$
factors through
$G \hookrightarrow J[r]$
factors through
![]() $\mathcal {FJ}[r]_K$
, then the schematic closure
$\mathcal {FJ}[r]_K$
, then the schematic closure
![]() $\overline {G}$
of G in
$\overline {G}$
of G in
![]() $\mathcal {J}[r]$
is finite and flat by Lemma 3.5, and it follows from Corollary 3.4 that the torsor extends into a logarithmic
$\mathcal {J}[r]$
is finite and flat by Lemma 3.5, and it follows from Corollary 3.4 that the torsor extends into a logarithmic
![]() $\overline {G}^D$
-torsor over
$\overline {G}^D$
-torsor over
![]() $\mathcal {C}$
. On the other hand, if there exists a finite flat model
$\mathcal {C}$
. On the other hand, if there exists a finite flat model
![]() $\mathcal {G}$
of G such that the torsor extends into a log
$\mathcal {G}$
of G such that the torsor extends into a log
![]() $\mathcal {G}^D$
-torsor, then it follows from Corollary 3.4 again that the K-morphism
$\mathcal {G}^D$
-torsor, then it follows from Corollary 3.4 again that the K-morphism
![]() $G \to J[r]$
extends into an R-morphism
$G \to J[r]$
extends into an R-morphism
![]() $\mathcal {G} \to \mathcal {J}[r]$
. Since
$\mathcal {G} \to \mathcal {J}[r]$
. Since
![]() $\mathcal {J}$
is separated, it follows that
$\mathcal {J}$
is separated, it follows that
![]() $\mathcal {G}$
is necessarily the schematic closure of G in
$\mathcal {G}$
is necessarily the schematic closure of G in
![]() $\mathcal {J}[r]$
; hence, by Lemma 3.5, it implies that
$\mathcal {J}[r]$
; hence, by Lemma 3.5, it implies that
![]() $G \hookrightarrow J[r]$
factors through
$G \hookrightarrow J[r]$
factors through
![]() $\mathcal {FJ}[r]_K$
.
$\mathcal {FJ}[r]_K$
.
Counter-example 3.7. Let A be a local Noetherian and complete ring, with fraction field K, and residue field of characteristics p. We find in [Reference Tate and Oort15, §5] the following bijection:
where
![]() $(a,b)\sim (c,d)$
if and only if
$(a,b)\sim (c,d)$
if and only if
![]() $\exists u \in A^{\times }$
such that
$\exists u \in A^{\times }$
such that
![]() $c=u^{p-1}a$
and
$c=u^{p-1}a$
and
![]() $d=u^{1-p}b$
. Considering the restriction morphism
$d=u^{1-p}b$
. Considering the restriction morphism
and taking, for example,
![]() $A=\mathbb {Z}_p$
, it is easy to see that
$A=\mathbb {Z}_p$
, it is easy to see that
![]() $\varphi $
is not surjective in general, which means that there are
$\varphi $
is not surjective in general, which means that there are
![]() $\mathbb {Q}_p$
-group schemes that does not extend into a finite flat
$\mathbb {Q}_p$
-group schemes that does not extend into a finite flat
![]() $\mathbb {Z}_p$
-group schemes.
$\mathbb {Z}_p$
-group schemes.
Question. More generally, it is natural to ask what happens if we do not assume that the structural group of the torsor admits a finite flat R-model. We investigate this question in the next section.
4. Part II: Extension of torsors under a quasi-finite flat group scheme
The following result by Antei says that there exists some regular model of the curve where the torsor extends into an fppf torsor.
Theorem 4.1 [Reference Antei and Emsalem2, Th. 3.7]
Let
![]() $\mathcal {X} \to \operatorname {\mathrm {Spec}}(R)$
be a faithfully flat morphism of finite type, with
$\mathcal {X} \to \operatorname {\mathrm {Spec}}(R)$
be a faithfully flat morphism of finite type, with
![]() $\mathcal {X}$
a regular and integral scheme of absolute dimension
$\mathcal {X}$
a regular and integral scheme of absolute dimension
![]() $2$
endowed with an R-section. Let G be a finite K-group scheme, and let
$2$
endowed with an R-section. Let G be a finite K-group scheme, and let
![]() $f:Y\to \mathcal {X}_K$
be an fppf pointed G-torsor. Then there exists an integral scheme
$f:Y\to \mathcal {X}_K$
be an fppf pointed G-torsor. Then there exists an integral scheme
![]() $\mathcal {X}_0$
, faithfully flat and of finite type over R, a model map
$\mathcal {X}_0$
, faithfully flat and of finite type over R, a model map
![]() $\lambda : \mathcal {X}_0 \to \mathcal {X}$
and an fppf
$\lambda : \mathcal {X}_0 \to \mathcal {X}$
and an fppf
![]() $\mathcal {G}$
-torsor
$\mathcal {G}$
-torsor
![]() $\mathcal {Y} \to \mathcal {X}_0$
extending the given G-torsor Y for some quasi-finite and flat R-group scheme
$\mathcal {Y} \to \mathcal {X}_0$
extending the given G-torsor Y for some quasi-finite and flat R-group scheme
![]() $\mathcal {G}$
. Moreover,
$\mathcal {G}$
. Moreover,
![]() $\mathcal {X}_0$
can be obtained by
$\mathcal {X}_0$
can be obtained by
![]() $\mathcal {X}$
after a finite number of Néron blow-ups.
$\mathcal {X}$
after a finite number of Néron blow-ups.
On the other hand, it is shown in [Reference Phung and Santos16] that an fppf torsor under a quasi-finite flat group scheme reduces into a torsor under a finite flat group scheme.
Theorem 4.2 [Reference Phung and Santos16, Th. 12.1]
Let R be a discrete valuation ring which is assumed to be Henselian Japanese, such that its residue field k is perfect. Let
![]() $\mathcal {X}$
be a normal, irreducible, projective, and flat R-scheme with geometrically reduced fibers and with an R-section. Let
$\mathcal {X}$
be a normal, irreducible, projective, and flat R-scheme with geometrically reduced fibers and with an R-section. Let
![]() $\mathcal {G}$
be a quasi-finite flat R-group scheme, and let
$\mathcal {G}$
be a quasi-finite flat R-group scheme, and let
![]() $\mathcal {Y} \to \mathcal {X}$
be a pointed fppf
$\mathcal {Y} \to \mathcal {X}$
be a pointed fppf
![]() $\mathcal {G}$
-torsor. Then, there exist a finite flat R-group scheme
$\mathcal {G}$
-torsor. Then, there exist a finite flat R-group scheme
![]() $\mathcal {H}$
, a morphism
$\mathcal {H}$
, a morphism
![]() $\mathcal {H} \to \mathcal {G}$
, and a pointed fppf
$\mathcal {H} \to \mathcal {G}$
, and a pointed fppf
![]() $\mathcal {H}$
-torsor
$\mathcal {H}$
-torsor
![]() $\mathcal {Y}_0 \to \mathcal {X}$
such that
$\mathcal {Y}_0 \to \mathcal {X}$
such that
![]() $\mathcal {Y}_0 \times ^{\mathcal {H}} \mathcal {G} \simeq \mathcal {Y}$
is pointed fppf
$\mathcal {Y}_0 \times ^{\mathcal {H}} \mathcal {G} \simeq \mathcal {Y}$
is pointed fppf
![]() $\mathcal {G}$
-torsors.
$\mathcal {G}$
-torsors.
We deduce from it the following.
Corollary 4.3. With the same notations and assumptions as in Theorem 4.2, if
![]() $\mathcal {Y} \to \mathcal {X}$
is a pointed fppf
$\mathcal {Y} \to \mathcal {X}$
is a pointed fppf
![]() $\mathcal {G}$
-torsor and
$\mathcal {G}$
-torsor and
![]() $\mathcal {F}$
the largest finite subgroup scheme inside
$\mathcal {F}$
the largest finite subgroup scheme inside
![]() $\mathcal {G}$
, there exists a pointed fppf
$\mathcal {G}$
, there exists a pointed fppf
![]() $\mathcal {F}$
-torsor
$\mathcal {F}$
-torsor
![]() $\mathcal {Y}_0 \to \mathcal {X}$
such that
$\mathcal {Y}_0 \to \mathcal {X}$
such that
![]() $\mathcal {Y}_0 \times ^{\mathcal {F}} \mathcal {G} \simeq \mathcal {Y}$
as pointed fppf
$\mathcal {Y}_0 \times ^{\mathcal {F}} \mathcal {G} \simeq \mathcal {Y}$
as pointed fppf
![]() $\mathcal {G}$
-torsors.
$\mathcal {G}$
-torsors.
Proof. Let
![]() $\mathcal {H}$
be the finite group scheme in Theorem 4.2. Since
$\mathcal {H}$
be the finite group scheme in Theorem 4.2. Since
![]() $\mathcal {F}$
is the largest finite subgroup of
$\mathcal {F}$
is the largest finite subgroup of
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\mathcal {H} \to \mathcal {G}$
factors through
$\mathcal {H} \to \mathcal {G}$
factors through
![]() $\mathcal {F}$
. Therefore, the surjective map
$\mathcal {F}$
. Therefore, the surjective map
 $$ \begin{align*} H^1_{fppf}(\mathcal{X},\mathcal{H}) & \to H^1_{fppf}(\mathcal{X},\mathcal{G})\\ \mathcal{T} &\mapsto \mathcal{T} \times^{\mathcal{H}} \mathcal{G} \end{align*} $$
$$ \begin{align*} H^1_{fppf}(\mathcal{X},\mathcal{H}) & \to H^1_{fppf}(\mathcal{X},\mathcal{G})\\ \mathcal{T} &\mapsto \mathcal{T} \times^{\mathcal{H}} \mathcal{G} \end{align*} $$
factors through
![]() $H^1_{fppf}(\mathcal {X},\mathcal {F})$
in an obvious way.
$H^1_{fppf}(\mathcal {X},\mathcal {F})$
in an obvious way.
Theorem 4.4. Let C be a smooth projective and geometrically connected K-curve with a K-point. Let
![]() $\mathcal {C}$
be a regular model of C, and let G be a finite commutative K-group scheme. Let
$\mathcal {C}$
be a regular model of C, and let G be a finite commutative K-group scheme. Let
![]() $Y \to C$
be an fppf pointed G-torsor. Then, there exist a quasi-finite flat group scheme
$Y \to C$
be an fppf pointed G-torsor. Then, there exist a quasi-finite flat group scheme
![]() $\mathcal {G}$
over R with generic fiber G and an fppf pointed
$\mathcal {G}$
over R with generic fiber G and an fppf pointed
![]() $\mathcal {G}$
-torsor over
$\mathcal {G}$
-torsor over
![]() $\mathcal {C}$
that extends the G-torsor
$\mathcal {C}$
that extends the G-torsor
![]() $Y \to C$
.
$Y \to C$
.
Proof. By Theorem 4.1, there exists a quasi-finite flat R-group scheme
![]() $\mathcal {G}$
that extends G, together with a regular model
$\mathcal {G}$
that extends G, together with a regular model
![]() $\mathcal {C}_0$
of C such that the fppf pointed G-torsor
$\mathcal {C}_0$
of C such that the fppf pointed G-torsor
![]() $Y \to C$
extends into an fppf
$Y \to C$
extends into an fppf
![]() $\mathcal {G}$
-torsor
$\mathcal {G}$
-torsor
![]() $\mathcal {Y} \to \mathcal {C}_0$
. By Corollary 4.3, if
$\mathcal {Y} \to \mathcal {C}_0$
. By Corollary 4.3, if
![]() $\mathcal {F}$
is the largest finite subgroup scheme of
$\mathcal {F}$
is the largest finite subgroup scheme of
![]() $\mathcal {G}$
, there exists a pointed fppf
$\mathcal {G}$
, there exists a pointed fppf
![]() $\mathcal {F}$
-torsor
$\mathcal {F}$
-torsor
![]() $\mathcal {Y}_0 \to \mathcal {C}_0$
such that
$\mathcal {Y}_0 \to \mathcal {C}_0$
such that
![]() $\mathcal {Y}_0 \times ^{\mathcal {F}} \mathcal {G}\simeq \mathcal {Y}$
. Hence, the pointed fppf
$\mathcal {Y}_0 \times ^{\mathcal {F}} \mathcal {G}\simeq \mathcal {Y}$
. Hence, the pointed fppf
![]() $\mathcal {F}_K$
-torsor
$\mathcal {F}_K$
-torsor
![]() $\mathcal {Y}_{0,K} \to C$
extends into the pointed fppf
$\mathcal {Y}_{0,K} \to C$
extends into the pointed fppf
![]() $\mathcal {F}$
-torsor
$\mathcal {F}$
-torsor
![]() $\mathcal {Y}_0 \to \mathcal {C}_0$
. If J denotes the Jacobian of C and
$\mathcal {Y}_0 \to \mathcal {C}_0$
. If J denotes the Jacobian of C and
![]() $\mathcal {J}^0$
the identity component of its Néron model, this is equivalent by Proposition 2.5 to the fact that the associated K-morphism
$\mathcal {J}^0$
the identity component of its Néron model, this is equivalent by Proposition 2.5 to the fact that the associated K-morphism
![]() $\mathcal {F}_K^D \to J$
(cf.(⋆)) extends into an R-morphism
$\mathcal {F}_K^D \to J$
(cf.(⋆)) extends into an R-morphism
![]() $\mathcal {F}^D \to \mathcal {J}^0$
. But this implies by Proposition 2.5 again that the fppf
$\mathcal {F}^D \to \mathcal {J}^0$
. But this implies by Proposition 2.5 again that the fppf
![]() $\mathcal {F}_K$
-torsor
$\mathcal {F}_K$
-torsor
![]() $\mathcal {Y}_{0,K} \to C$
extends into an fppf
$\mathcal {Y}_{0,K} \to C$
extends into an fppf
![]() $\mathcal {F}$
-torsor
$\mathcal {F}$
-torsor
![]() $\mathcal {Y}' \to \mathcal {C}$
. Hence, the G-torsor
$\mathcal {Y}' \to \mathcal {C}$
. Hence, the G-torsor
![]() $Y \to C$
extends into the fppf
$Y \to C$
extends into the fppf
![]() $\mathcal {G}$
-torsor
$\mathcal {G}$
-torsor
![]() $\mathcal {Y}' \times ^{\mathcal {F}} \mathcal {G} \to \mathcal {C}$
.
$\mathcal {Y}' \times ^{\mathcal {F}} \mathcal {G} \to \mathcal {C}$
.
Acknowledgements
The author would like to thank her thesis advisors Jean Gillibert and Dajano Tossici for their constant support, encouragements, and the mathematical discussions with them. She would also like to thank Thibault Poiret with whom it was very fruitful to discuss and who notably helped her to understand some points of [Reference Holmes, Molcho, Orecchia and Poiret5] that he co-wrote.