Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
1995.
Vol. 182,
Issue. ,
p.
887.
1996.
Vol. 183,
Issue. ,
p.
889.
Carvalho, Paula A.A.B.
2005.
ON THE AZUMAYA LOCUS OF SOME CROSSED PRODUCTS#.
Communications in Algebra,
Vol. 33,
Issue. 1,
p.
51.
Jiang, Xiaolong
Kuo, Jung-Miao
and
Szeto, George
2018.
On Partial Galois Algebras.
Taiwanese Journal of Mathematics,
Vol. 22,
Issue. 6,
Paques, Antonio
2018.
Advances in Mathematics and Applications.
p.
247.
Jiang, Xiaolong
Kuo, Jung-Miao
and
Szeto, George
2020.
On three special types of partial Galois extensions.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 12,
p.
2150004.


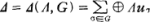 be the crossed product of
be the crossed product of 