Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ding, Yong
Xue, Qingying
and
Yabuta, Kôzô
2006.
Existence and Boundedness of Parametrized Marcinkiewicz Integral with Rough Kernel on Campanato Spaces.
Nagoya Mathematical Journal,
Vol. 181,
Issue. ,
p.
103.
Zhang, Songyan
and
Tao, Xiangxing
2010.
Boundedness of Littlewood-Paley Operators in Generalized Orlicz-Campanato Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 40,
Issue. 4,
Meng, Yan
Nakai, Eiichi
and
Yang, Dachun
2010.
Estimates for Lusin-area and Littlewood–Paley functions over spaces of homogeneous type.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 5,
p.
2721.
He, Sha
Xue, Qingying
Mei, Ting
and
Yabuta, Kôzô
2015.
Existence and boundedness of multilinear Littlewood–Paley operators on Campanato spaces.
Journal of Mathematical Analysis and Applications,
Vol. 432,
Issue. 1,
p.
86.
Li, Xiang
He, Qianjun
and
Yan, Dunyan
2020.
Boundedness of Multilinear Littlewood-Paley Operators on Amalgam-Campanato Spaces.
Acta Mathematica Scientia,
Vol. 40,
Issue. 1,
p.
272.
Jia, Hongchao
Yang, Dachun
Yuan, Wen
and
Zhang, Yangyang
2023.
Estimates for Littlewood–Paley Operators on Ball Campanato-Type Function Spaces.
Results in Mathematics,
Vol. 78,
Issue. 1,
Lin, Qingze
Liu, Hongshen
and
Song, Liang
2025.
The Behavior of Hardy–Littlewood Maximal Operator and Littlewood–Paley Operators on CMO Space.
Tokyo Journal of Mathematics,
Vol. 48,
Issue. 1,

 . We prove that if
. We prove that if 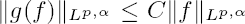 . Thus we give an improvement of some earlier results such as in [8], where it is always needed to assume
. Thus we give an improvement of some earlier results such as in [8], where it is always needed to assume 