Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakai, Mitsuru
and
Sario, Leo
1966.
Normal operators, linear liftings and the Wiener compactification.
Bulletin of the American Mathematical Society,
Vol. 72,
Issue. 6,
p.
947.

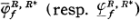 the totality of lower bounded superharmonic (resp. upper bounded subharmonic) functions soni
the totality of lower bounded superharmonic (resp. upper bounded subharmonic) functions soni