Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T04:22:22.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results on Finite Groups Whose Order Contains a Prime to the First Power

Published online by Cambridge University Press:  22 January 2016

Richard Brauer
Richard Brauer*
Affiliation:
Harvard University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous investigation [1], the author has studied finite groups 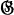of an order g = pg 0 where p is a prime and g 0 an integer not divisible by p. This work has been continued by H. F. Tuan [5]. Let t denote the number of conjugate classes of 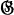which consist of element of order p. Tuan dealt with the groups 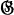for which t≦2 and which have a faithful representation of degree less than p - 1. We shall assume here that t≧3. We shall also suppose that 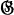does not have a normal subgroup of order p. We state here two results. We shall show (Corollary, Theorem 1) that if / is a faithful irreducible character of 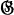of degree n which has T>1 conjugates over the field of the g 0-th roots of unity, then

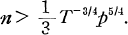
Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 27 , Issue 2 , July 1966 , pp. 381 - 399
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Brauer, R., On groups whose order contains a prime number to the first power, I, II. American Journal of Mathematics 64 (1942), 401–420, 421–440.Google Scholar
[2] Brauer, R., A characterization of the characters of groups of finite order, Annals of Mathematics 57 (1953), 357–377.Google Scholar
[3] Brauer, R., Some applications of the theory of blocks of characters of finite groups, I. Journal of Algebra 1 (1964), 152–167.Google Scholar
[4] Brauer, R. and Nesbitt, C., On the modular characters of groups, Annals of Mathematics 52 (1941), 556–590.CrossRefGoogle Scholar
[5] Tuan, H. F., On groups whose order contains a prime to the first power, Annals of Mathematics 45 (1944), 110–140.Google Scholar