Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yano, Kentaro
1957.
Sur Un Théorème de M. Matsushima.
Nagoya Mathematical Journal,
Vol. 12,
Issue. ,
p.
147.
Tachibana, Shun-ichi
1959.
On almost-analytic vectors in almost-Kählerian manifolds.
Tohoku Mathematical Journal,
Vol. 11,
Issue. 2,
Goldberg, S. I.
1960.
Groups of automorphisms of almost Kaehler manifolds.
Bulletin of the American Mathematical Society,
Vol. 66,
Issue. 3,
p.
180.
Tachibana, Shun-ichi
and
Ishihara, Shigeru
1960.
On infinitesimal holomorphically projective transformations in Kählerian manifolds.
Tohoku Mathematical Journal,
Vol. 12,
Issue. 1,
Ise, Mikio
1960.
Some properties of complex analytic vector bundles over compact complex homogeneous spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 36,
Issue. 5,
Sawaki, Sumio
1961.
On the Matsushima's theorem in a compact Einstein $K$-space.
Tohoku Mathematical Journal,
Vol. 13,
Issue. 3,
Nomizu, Katsumi
1961.
Recent development in the theory of connections and holonomy groups.
Advances in Mathematics,
Vol. 1,
Issue. 1,
p.
1.
Sawaki, Sumio
1962.
A generalization of Matsushima's theorem.
Mathematische Annalen,
Vol. 146,
Issue. 4,
p.
279.
1962.
Vol. 11,
Issue. ,
p.
303.
Takamatsu, Kichiro
1964.
On a decomposition of an almost-analytic vector in a $K$-space with constant scalar curvature.
Tohoku Mathematical Journal,
Vol. 16,
Issue. 1,
Kobayashi, Shoshichi
1967.
Imbeddings of homogeneous spaces with minimum total curvature.
Tohoku Mathematical Journal,
Vol. 19,
Issue. 1,
Ogawa, Yôsuke
1968.
On contravariant $C$-analytic $1$-forms in a compact Sasakian space.
Tohoku Mathematical Journal,
Vol. 20,
Issue. 3,
Takamatsu, Kichiro
1968.
On a decomposition of an extended contravariant almost analytic vector in a compact $K$-space with constant scalar curvature.
Kodai Mathematical Journal,
Vol. 20,
Issue. 2,
Tanno, Shûkichi
1969.
The automorphism groups of almost Hermitian manifolds.
Transactions of the American Mathematical Society,
Vol. 137,
Issue. 0,
p.
269.
Matsushima, Yozo
1972.
Remarks on Kähler-Einstein Manifolds.
Nagoya Mathematical Journal,
Vol. 46,
Issue. ,
p.
161.
Sommese, Andrew John
1975.
Quaternionic manifolds.
Mathematische Annalen,
Vol. 212,
Issue. 3,
p.
191.
Sakane, Yusuke
1981.
Manifolds and Lie Groups.
p.
337.
Futaki, Akito
1983.
On compact Kähler manifolds of constant scalar curvatures.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 59,
Issue. 8,
Salamon, Simon
1983.
Geometry Seminar “Luigi Bianchi”.
Vol. 1022,
Issue. ,
p.
33.
Futaki, A.
1983.
An obstruction to the existence of Einstein K�hler metrics.
Inventiones Mathematicae,
Vol. 73,
Issue. 3,
p.
437.

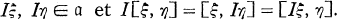 On peut donc définir une structure d’algèbre de Lie complexe de α en posant
On peut donc définir une structure d’algèbre de Lie complexe de α en posant 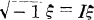 pour tout
pour tout 