Contents
Research Article
On Segregated Rings and Algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-7
-
- Article
-
- You have access
- Export citation
On the Dimension of Modules and Algebras, V. Dimension of Residue Rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 9-12
-
- Article
-
- You have access
- Export citation
On the Theory of Differential Forms on Algebraic Varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-39
-
- Article
-
- You have access
- Export citation
On the Transition Probability of a Renewal Process
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-51
-
- Article
-
- You have access
- Export citation
Sur les Espaces Homogènes Kählériens d’un Groupe de Lie Réductif
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 53-60
-
- Article
-
- You have access
- Export citation
On the Dimension of Modules and Algebras, VI. Comparison of Global and Algebra Dimension
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-65
-
- Article
-
- You have access
- Export citation
On the Dimension of Modules and Algebras, VII. Algebras with Finite-Dimensional Residue-Algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 67-76
-
- Article
-
- You have access
- Export citation
Some Studies on Kaehlerian Homogeneous Spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 77-92
-
- Article
-
- You have access
- Export citation
Canonical Connections and Pontrjagin Classes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 93-109
-
- Article
-
- You have access
- Export citation
On Infinitesimal Holonomy and Isotropy Groups
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 111-114
-
- Article
-
- You have access
- Export citation
On Automorphisms of A Kählerian Structure
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 115-124
-
- Article
-
- You have access
- Export citation
On Algebraic Groups Defined by Norm Forms of Separable Extensions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 125-130
-
- Article
-
- You have access
- Export citation
Sur les Ensembles d’Accumulation Relatifs à des Transformations Localement Pseudo-Analytiques au Sens de Pfluger-Ahlfors
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 131-144
-
- Article
-
- You have access
- Export citation
Sur la Structure du Groupe d’Homéomorphismes Analytiques d’une Certaine Variété Kaehlérinne
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-150
-
- Article
-
- You have access
- Export citation
Capacité d’Ensembles de Cantor Généralisés*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 151-160
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 11 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 11 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation
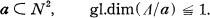
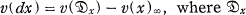 is the different-divisor (Verzweigungsdivisor) of
is the different-divisor (Verzweigungsdivisor) of 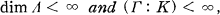
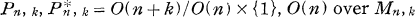 and the invariant Riemannian connection on
and the invariant Riemannian connection on 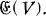 Let
Let  becomes an algebraic group if
becomes an algebraic group if 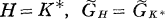 will mean the group of linear transformations of
will mean the group of linear transformations of 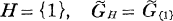 will mean the group of linear transformations of
will mean the group of linear transformations of 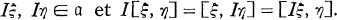 On peut donc définir une structure d’algèbre de Lie complexe de α en posant
On peut donc définir une structure d’algèbre de Lie complexe de α en posant 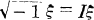 pour tout
pour tout  qui restent, puis on applique la 3-opération à chacun des intervalles
qui restent, puis on applique la 3-opération à chacun des intervalles 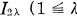
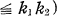 qui restent, et ainsi de suite. On appellera l’ensemble limite restant un
qui restent, et ainsi de suite. On appellera l’ensemble limite restant un 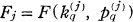 un ensemble de Cantor généralisé défini sur l’axe de
un ensemble de Cantor généralisé défini sur l’axe de