No CrossRef data available.
Published online by Cambridge University Press: 22 January 2016
Dans tout ce qui suit, les varietés qui interviendront seront définies sur le corps des nombres complexes C. L’objet de cet article est de préciser le résultat suivant obtenu dans [B-2] et [K-1]:
Théorème 0. Soit X une variété protective normale de dimension 3, dont les singularités sont canoniques au sens de [R-1]. Soient e le p.p.c.m. des indices des points singuliers de X. Soit R un diviseur de Cartier sur X, tel que le bidual de 
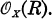 Supposons que R soit numériquement positif et que R3 > 0. Alors il existe un entier n0 > 0 tel que pour tout
Supposons que R soit numériquement positif et que R3 > 0. Alors il existe un entier n0 > 0 tel que pour tout 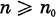 le système linéaire |nR| soit sans point base; en particulier l’anneau
le système linéaire |nR| soit sans point base; en particulier l’anneau 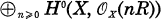 est de type fini sur C.
est de type fini sur C.