Contents
Research Article
A classification of Riemannian 3-manifolds with constant principal ricci curvaturesρ1= ρ2≠ ρ3
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-36
-
- Article
-
- You have access
- Export citation
Generators for a maximally differential ideal in positive characteristic
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
Reductibility and irreducibility of the Gauss-Manin system associated with a Selberg type integral
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 43-62
-
- Article
-
- You have access
- Export citation
Centroaffine immersions of codimension two and projective hypersurface theory
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 63-90
-
- Article
-
- You have access
- Export citation
Zeta functions of prehomogeneous affine spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-114
-
- Article
-
- You have access
- Export citation
Algebraic threefolds with two extremal morphisms
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 115-129
-
- Article
-
- You have access
- Export citation
P-harmonic dimensions on ends
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 131-139
-
- Article
-
- You have access
- Export citation
Oscillation of modes of some semi-stable Lévy processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 141-153
-
- Article
-
- You have access
- Export citation
Complete conformal metrics with prescribed scalar curvature on subdomains of a compact manifold
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 155-173
-
- Article
-
- You have access
- Export citation
New invariants and class number problem in real quadratic fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 175-197
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 132 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 132 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation
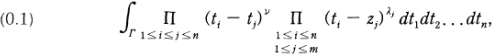
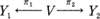
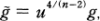 where
where