Let us begin by recalling the existence of optimal controls for a class of stochastic differential equations

with given initial condition X(0) = x, where B is an n-dimensional Brownian motion and the control U is a stochastic process. As admissible controls, let us allow all non-anticipative process U(t) = (U1(t),…Um(t)) ∈ Γ where Γ is a compact subset of Rm. We call Γ a control region. Assume that the matrix valued functional β and the n-vector valued α satisfy a Lipscitz condition in X and some growth condition. Then we have a unique solution Xu for an admissible control U.

In this note we exhibit an interpolant for a certain valid implication ╞ φ → ψ, where φ and ψ come from the infinitary language Lω1ω1. The existence of this interpolant follows from Takeuti’s heterogeneous interpolation theorem [5], but unfortunately the proof in [5] is not explicit enough to allow one to find the interpolant explicitly. Takeuti’s theorem asserts the existence of an interpolant in the class Lω1ω1 of heterogeneous formulas, which admits the rules of formation of Lω1ω1 plus the following additional rule:

Es ist wichtig und interessant, die Beziehungen zwischen Krümmung, Volumen, Geodätischen und topologischen Strukturen von Riemannschen Mannigfaltigkeiten mit positiver Krümmung zu untersuchen.

The aim of this paper is to discuss the multiplicity of the sum of two independent Gaussian processes

where x1(t) is a Wiener process and is a simple Markov process.

In Umemura [9], we calculated the invariants algcd (G), p(G), q(G) for a commutative algebraic group G. We remark that all the results hold for a group scheme which is not necessarily commutative.

To determine p(G), I cannot succeed in dropping the hypothesis “quasi-projective” but this assumption is satisfied in the characteristic 0 case.

Let M, N be connected complex submanifolds of a neighborhood of the origin 0 ∈ Cd, the space of d complex variables, such that 0 ∈ M ∩ N. We shall suppose throughout that M ⊄ N and N ⊄ M in any neighborhood of 0. Let X = M ∪ N. X is an analytic subvariety with the irreducible branches M and N. Let Δ be a neighborhood of 0 in Cd.

In the article I: [8], we have proved the hypoellipticity of a degenerate parabolic equation of the form:

where the coefficients a(x, t), b(x,t) and c(x, t) are complex valued smooth functions. The fundamental assumption on the coefficients is that Re a(x, t) satisfies the condition of Nirenberg and Treves ([8], (1.5)). To prove the hypoellipticity we have constructed recurcively the parametrices as pseudodifferential operators with parameter. This method may be viewed as an improvement of that of [9] and [7]. We have analyzed the properties of these parametrices by estimating the symbols with parameter associated with the given operator. We shall summerize these results in §3.

In [1] and [2], Hironaka referred to the importance of an additive group scheme BPn,P, which is associated with a point p in Pn, in connection with the resolution of singularities in characteristic p > 0. Also he showed that if the dimension of BPn,p is not greater than p, then it is a vector group.

We have several definitions of the positivity of a vector bundle, differentiate definitions, an algebro-geometric definition, a topological definition etc. In § 1 we review the definitions and the relations between them. For a line bundle all the definitions are equivalent and every one agrees that they are reasonable. For a vector bundle, however, the definitions are not necessarily equivalent. One of the main results of this paper is the equivalence of the definitions over a complete non-singular curve. The proof is given in §2. We proved this over an elliptic curve in Umemura [18]. In this case the proof was based on Atiyah’s classification. To prove the equivalence over a curve of genus ≥ 2, the fundamental lemma is; A stable bundle of positive degree is positive in the sense of Nakano. The tool used to prove this lemma is the theory of stable bundles due to Narasimhan and Seshadri [11] —they establish a correspondence between stable bundles and certain types of irreducible unitary representations of a Fuchsian group.

Let X be a non-singular projective surface in (k an algebraically closed field of characteristic 0) and C an irreducible curve, which is a set-theoretically complete intersection in X; is it true that C is actually a complete intersection in X?

In this paper we consider a class of nonanalytic automorphic functions which were first mentioned to A. Selberg by C. L. Siegel. These functions have Fourier coefficients which are closely connected with the Fourier coefficients of analytic automorphic forms, and they are also eigenfunctions of the Laplace operator derived from the hyperbolic metric. We shall show how this latter property gives new results in the classical theory of automorphic forms.

In this note we study quaternary even positive definite quadratic forms of prime discriminant. In § 1 we classify quaternary even positive definite quadratic forms of prime discriminant p = 1 mod 4 (called simply nice quaternary lattices in this note) which represent two. We note that the class number of such forms is closely related to the dimension of the space of certain automorphic forms. (Remark 4 in the text). By using the classification in § 1 and the theory of integral representations of cyclic groups we show that the orthogonal group of a nice quaternary lattice is generated by ±1 and symmetries (of the lattice). In § 3, we calculate the class number of nice quaternary lattices. Notations and terminologies will generally be those of O’Meara [5]. Any exceptions to this convention will be stated explicitly.

We treat the sum 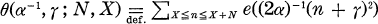, where α and γ are real with α positive. This sum was treated first by Hardy and Littlewood [4], and after them, by Behnke [1] and [2], Mordell [9], Wilton [11] and others. The reader will find its history in [7] and in the comments of the Collected Papers [4]. Here we show that the sum can be expressed explicitly, together with an error term O(N1/2), using the regular continued fraction expansion of α. As the statements have complications we will divide them into two theorems. In the followings all letters except ϑ, i, σ, ζ, χ and those in 3° are real, N is a positive real, and always k, n, a, A, B, C, D and E denote integers. The author expresses his thanks to Professor Tikao Tatuzawa and Professor Tomio Kubota for their encouragements.

This paper is a continuation of “Stable vector bundles on algebraic surfaces” [10]. For simplicity we deal with non-singular projective varieties over the field of complex numbers. Let W be a variety whose fundamental group is solvable, let H be an ample line bundle on W, and let f: V → W be an unramified covering. Then we show in section 1 that if E is an f*H-stable vector bundle on V then f*E is a direct sum of H-stable vector bundles. In particular f*L is a direct sum of simple vector bundles if L is a line bundle on V.

Let Mg be the coarse moduli space of complete non-singular curves of genus g and the coarse moduli space of principally polarized abelian varieties of dimension g. There is a canonical map: