Contents
Research Article
Regular Tsuji Functions with Infinitely Many Julia Points
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-196
-
- Article
-
- You have access
- Export citation
A Boundary Theorem for Tsuji Functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 197-200
-
- Article
-
- You have access
- Export citation
A Method of Two-Level Simplification of Boolean Functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 201-210
-
- Article
-
- You have access
- Export citation
Finite Dimensional Approximation to Band Limited White Noise
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 211-216
-
- Article
-
- You have access
- Export citation
Some Remarks in the Fourier Analysis
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 217-219
-
- Article
-
- You have access
- Export citation
On Mean Distortion for Analytic Functions with Positive Real Part in a Circle
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 221-228
-
- Article
-
- You have access
- Export citation
On the Balayage for Logarithmic Potentials
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 229-241
-
- Article
-
- You have access
- Export citation
Planar Coverings of Closed Riemann Surfaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 243-257
-
- Article
-
- You have access
- Export citation
A Note on Tangent Bundles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 259-267
-
- Article
-
- You have access
- Export citation
Remark on the Dual EHP Sequence
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 269-280
-
- Article
-
- You have access
- Export citation
The Genus Field and Genus Number in Algebraic Number Fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 281-285
-
- Article
-
- You have access
- Export citation
On the Non-Minimal Martin Boundary Points
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 287-290
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 29 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f8
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 29 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
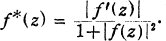


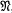 be the class of analytic functions Ф(
be the class of analytic functions Ф(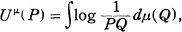
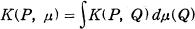
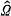 and the kernel
and the kernel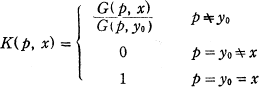
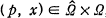 , where
, where 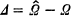 is divided into two disjoint subsets Δ
is divided into two disjoint subsets Δ