Silicon stable isotope fractionation between metal and silicate at high-pressure, high-temperature conditions as a tracer of planetary core formation

Abstract

The largest differentiation event in Earth and other terrestrial planets was the high-pressure, high-temperature process of metal core segregation from a silicate mantle. The abundant element silicon (Si) can be partially sequestered into the metallic core during metal–silicate differentiation, depending on pressure, temperature and planetary oxidation state. Knowledge of the Si content of a planet's core can constrain the conditions of core formation, but in the absence of direct samples from planetary cores, quantifying core Si content is challenging. One relatively new tool to study core formation in terrestrial planets is based on combining measurements of the Si stable isotopic composition of planetary crust and mantle samples with measurements of the Si stable isotope fractionation between metal and silicate at high-temperature and high-pressure conditions. In this study we present the results of a small set of high-pressure, high-temperature (HPT) experiments and combine these with a review of literature data to investigate how the Si isotope fractionation behaviour between metal and silicate varies as a function specifically of experimental run time and temperature. We show that although there is no debate about the sign of fractionation, absolute values for Si isotope fractionation between metal and silicate are difficult to constrain because the experimental database remains incomplete, and because Si isotopic measurements of metals in particular suffer from the absence of a true inter-laboratory comparison. We conclude that in order to derive accurate quantitative estimates of the Si content of the core of the Earth or other planets a wide range of additional experiments will be required.

Introduction

Planetary accretion and metallic core formation

Seismological data show that currently the Earth consists of a dense inner solid and outer liquid metallic core (Fig. 1), surrounded by a silicate shell (bulk silicate earth, BSE) comprising a mantle and a crust (e.g. Birch, 1952). This large-scale internal differentiation occurred within the first 100 million years of the formation of the solar system and the Earth, and is linked to early planetary accretion processes.

Fig. 1. Currently, the Earth is differentiated into a silicate shell (BSE) and an inner solidified and outer liquefied metallic core. The core--mantle boundary (CMB) is located between the outer metallic portion and the inner part of the silicate shell (inner mantle).

Planetary accretion proceeds by collisions of planetesimals and smaller planetary bodies on a timescale of thousands of years in the terrestrial planet zone of our solar system. Larger planetesimals grow by gravitationally sweeping up smaller ones, leading to larger bodies growing more rapidly than the smaller planetesimals. This so-called ‘runaway growth process’ (e.g. Kortenkamp et al., 2001; Inaba et al., 2001) led to the formation of several tens of Moon- to Mars-sized planetary embryos in the terrestrial planet zone. Final accretion of today's terrestrial planets took place through large impact events (e.g. Wetherill, 1985; Stevenson, 1990; Chambers, 2004; Wood & Halliday, 2005).

The kinetic energy of small and large collisions is converted into thermal energy. The build-up of heat, in combination with heat production through natural radioactive decay, led to widespread melting and the formation of deep magma oceans on most if not on all the terrestrial planets and the Moon (e.g. Yoshino et al., 2003; Rubie et al., 2003; Elkins-Tanton, 2012; Rai & Van Westrenen, 2013, 2014). As a consequence of large-scale melting, the planets, including the primitive Earth, differentiated into a dense metallic core and a siliceous mantle. Measurements comparing the tungsten isotopic compositions of chondritic meteorites and BSE indicate that the main stage of terrestrial core segregation probably took place between 30 and 60 Ma after the formation of the solar system (e.g. Yin et al., 2002; Burkhardt et al., 2008).

The geochemical and geophysical signature of the Earth and its core

Since it is impossible to obtain samples from the Earth's deepest interior, information on the Earth's bulk chemical composition and its core can only be acquired indirectly, by investigating meteorites and by sampling the accessible parts of the silicate Earth. Additional indirect evidence can be gained from seismic observations. These geochemical and geophysical investigations yield models for the composition of the BSE and the bulk earth (BE), from which the chemical composition of the core can be estimated using simple mass balance.

Chemical composition of BSE and BE.

Accretion and planetary differentiation have both influenced element abundances in the Earth's mantle. Based on element concentrations of the Earth's mantle derived from mantle xenoliths and Mid-Ocean Ridge Basalt analyses (e.g. Allègre et al., 1995; McDonough & Sun, 1995), it was found that BSE for many elements is chemically related to carbonaceous (CI) chondrites – the most primitive chondritic meteorites in our solar system, which are believed to form the main building blocks of Earth.

Geochemically distinct groups of elements show different degrees of depletion in the Earth's mantle compared to the composition of these CI chondrites. This observed depletion appears to depend in part on the elemental condensation temperatures (e.g. Lodders, 2003). Elements including Zr, Mg, and rare earth elements are lithophile and prefer to partition into silicates over metallic or sulphide phases. They are also non-volatile or refractory elements, and their relative abundances in BSE are comparable to their relative abundances in CI chondrites. These elements were not removed from the mantle by differentiation processes and were not lost before or during Earth formation by volatilisation. In contrast, more volatile lithophile elements are depleted from the Earth's mantle relative to CI chondrites either as a result of partial condensation from the solar nebula or due to their volatility during high-temperature planetary accretion processes.

The 50% condensation temperature of an element can approximate its volatility degree. By definition, this is the temperature at which half of the number of atoms of the element reside in a solid phase and half in the gas phase. Fig. 2 shows a simplified illustration of the observed abundances of lithophile elements and iron in the Earth's mantle, normalised to CI chondrite element abundances and Mg, versus their 50% condensation temperatures determined thermodynamically (data from McDonough, 2003; Lodders, 2003). The trend of decreasing abundance of moderately lithophile elements with decreasing 50% condensation temperature is called the Earth's volatility trend. With respect to the composition of the core it is assumed that the solid grey line in Fig. 2 defines the composition of the BE. The grey arrow at the left-hand side of Fig. 2 indicates the Earth's volatility trend.

Fig. 2. The abundance of lithophile elements (plus iron) in BSE normalised to CI chondrites and Mg (BSE abundances from McDonough, 2003; CI abundances from Lodders, 2003). BSE depletions of elements to abundances below the estimate for bulk Earth are assumed to be due to segregation of these elements into the Earth's core (e.g. iron). Relative to the magnesium concentration in CI chondrites and BSE, silicon also shows a slight depletion in the silicate portion of the Earth.

Geophysical constraints on core composition.

The presence of a core–mantle boundary (CMB) in the Earth was first suspected at a depth of 2900 km (Figs 1 and 3) by Oldham (1906) and was subsequently confirmed on the basis of seismic measurements and calculations by Gutenberg (1914) and Jeffreys (1935). Temperature estimates of today's Earth's core range from 4000 to 7000 K and pressures vary between 136 and 364 GPa from the CMB to the Earth's centre. The inner core consists of a solidified iron–nickel alloy. A primary feature of Earth's present-day liquid outer core is its so-called core density deficit (CDD), referring to the seismological observation that the outer core density is between 2.5% and 10% lower than expected for a molten iron–nickel alloy (Fig. 3; Birch, 1952, 1964; Anderson & Isaak, 2002).

Fig. 3. Density vs depth plot of the outer Earth's core region (2900–5150 km from Earth's surface). The comparison between measured core density (red line) and experimentally investigated density of pure Fe–Ni alloys at HPT conditions illustrates the core density deficit (CDD; blue field for iron-nickel melt; purple field for a solidified iron-nickel composition; green field for a partially molten iron-nickel composition; modified after Li & Fei, 2003).

The CDD can be explained by the incorporation of one or more light elements into the core (e.g. Poirier, 1994; Javoy, 1999; Dreibus & Palme, 1996; Li & Fei, 2003). In addition to sulfur (e.g. Brett, 1984), oxygen (e.g. Corgne et al., 2009), hydrogen (e.g. Okuchi, 1997) and carbon (e.g. Wood, 1993; Dasgupta & Walker, 2008), silicon has been proposed as a ‘key’ light element in the outer Earth's core (e.g. MacDonald & Knopoff, 1958; Birch, 1964; Ringwood, 1966; Tuff et al., 2011). The Earth is not unique in having light elements in its core: light elements are also known to be present in the cores of the Moon (e.g. Rai & Van Westrenen, 2014), Mars (e.g. Rai & Van Westrenen, 2013) and Mercury (e.g. Dumberry & Rivoldini, 2014; Knibbe & Van Westrenen, 2015), as well as differentiated asteroids such as Vesta (e.g. Steenstra et al., 2015). The nature and abundance of light elements in a planetary core provide a fingerprint for planetary core formation conditions, and therefore provide constraints on early planetary evolution. For example, Si can only be incorporated into metal at oxygen-poor (highly reducing) conditions – conditions that are not present in the Earth today. If Si is present in Earth's core, the Earth must have been much less oxygen-rich when its core formed than it is today.

The role of Si stable isotopes

Due to the advent of multi-collector (MC) ICPMS techniques, it has become possible in recent years to approach the specific question of Si incorporation into the core of the Earth and other planetary bodies by studying the distribution of Si stable isotopes (²⁸Si, ²⁹Si and ³⁰Si) between metals and silicates, either by comparing isotopic signatures of terrestrial and extra-terrestrial silicate samples or by measuring their distribution in coexisting metal and silicate phases equilibrated in experiments simulating conditions of core formation. Isotope-geochemical investigations of terrestrial mantle rocks, as well as lunar samples (summarised in Fig. 4), show slightly higher δ³⁰Si (δ³⁰Si = [((³⁰Si/²⁸Si_sample)/(³⁰Si/²⁸Si_standard)) – 1] × 1000 [‰]) values than undifferentiated meteorites (Georg et al., 2007; Fitoussi et al., 2009; Ziegler et al., 2010; Chakrabarti & Jacobsen, 2010; Armytage et al., 2011, 2012; Savage & Moynier, 2013; see recent compilation by Savage et al., 2014). The average δ³⁰Si isotopic signature of terrestrial mantle rocks is estimated to be –0.29‰ ± 0.07‰, 2_SD (Douthitt, 1982; Georg et al. 2007; Fitoussi et al., 2009; Ziegler et al., 2010; Savage et al., 2010; Chakrabarti & Jacobsen, 2010; Armytage et al., 2011, 2012; Savage & Moynier, 2013; Savage et al., 2014; see Fig. 4). The average δ³⁰Si isotopic signature for carbonaceous and ordinary chondrites (δ³⁰Si_CHUR) is –0.47‰ ± 0.06‰ (Molini-Velsko et al., 1986; Georg et al., 2007; Fitoussi et al., 2009; Chakrabarti & Jacobsen, 2010; Armytage et al., 2011, 2012; Fitoussi & Bourdon, 2012; Savage & Moynier, 2013; Savage et al., 2014; Fig. 4).

Fig. 4. Three-isotope diagram showing average isotope signatures of undifferentiated meteorites, BSE and lunar basalts (data from Georg et al., 2007; Fitoussi et al., 2009; Ziegler et al., 2010; Chakrabarti & Jacobsen, 2010; Armytage et al. 2011, 2012). The observed mass difference between Earth's building blocks (meteorites) and BSE is explained by Si equilibrium isotope fractionation between metal and silicate at high-temperature conditions. If Si would be a light element in the Earth's core, the metal would concentrate the light isotope fraction.

The absolute isotopic difference between CI chondrites and the BSE of Δ³⁰Si_BSE–CHUR = 0.18‰ ± 0.06‰ (where Δ³⁰Si_A–B = δ³⁰Si_A – δ³⁰Si_B) has been explained by equilibrium metal–silicate Si isotope fractionation at high-temperature and high-pressure (HPT) conditions at reducing oxygen conditions (e.g. Georg et al., 2007; Shahar et al., 2009, 2011; Ziegler et al., 2010; Kempl et al., 2013a; Hin et al., 2014), driven by the different chemical bonding environment of Si in silicate rocks versus metallic liquid (Schauble et al., 2007; Georg et al., 2007). If Si isotope fractionation between metal and silicate is an equilibrium process, the heavier isotopes fractionate preferentially into the stiffer bonded phase, in this case the silicate. Heavier Si isotopes fractionating into the silicate, and lighter isotopes fractionating into the metal was observed in meteorite samples that contain both metal and silicate phases: first in enstatite chondrites, comprising a Si-bearing metal and a silicate phase (Molini-Velsko et al., 1986), and subsequently by Ziegler et al. (2010), who assumed Si isotope equilibration between metal and silicate in two aubrite meteorites occurred through solid-state diffusion.

If metal–silicate equilibration is the cause of the observed difference between CI chondrites and BSE Si isotopic composition, (1) Si must be present in the Earth's core and (2) the Earth's core Si isotopic signature must be isotopically lighter than the Si isotopic signature of the BSE (Fig. 4).

Evidence for Si in the Earth's outer core

Geochemical and geophysical lines of evidence support the hypothesis that Si is one of the light elements in the outer Earth's core, but uncertainty about its concentration remains substantial. The latest geophysical models suggest that the Earth's core contains up to 4.5 wt% Si, in addition to significant amounts of oxygen (e.g. Badro et al., 2014). The experimental observation that Si becomes more siderophile with increasing pressure and temperature conditions and decreasing oxygen fugacity could explain the observed slight depletion of Si in the silicate portion of the Earth compared to its predicted BSE concentration using the Earth's volatility trend (Fig. 2).

The observed superchondritic Mg/Si and Al/Si ratios in the primitive upper mantle (e.g. Allègre et al., 1995; Drake & Righter, 2002) can be reconciled with chondritic models of bulk Earth composition by incorporating approximately 6 wt% of Si in the core (e.g. McDonough, 2003).

The experimentally determined element partitioning behaviour of Si and a range of other siderophile elements suggest the presence of anywhere between 1 and 11 wt% Si in the core (e.g. Ricolleau et al., 2011). Although this is qualitatively consistent with cosmochemical arguments, constraints from Si partitioning data are currently not precise enough to distinguish between different core formation scenarios.

Translation of the observed Si isotope fractionation between the BSE and the Earth's building blocks (~0.2 per mille in terms of Δ³⁰Si) into corresponding core Si concentrations requires knowledge of Si isotope fractionation factors between silicate and iron metal at HPT conditions. To date, these have mostly been predicted using theoretical calculations (e.g. Georg et al., 2007; Fitoussi et al., 2009; Ziegler et al., 2010; Chakrabarti & Jacobsen, 2010; Armytage et al., 2011), suggesting that the Si concentration in the Earth's outer core could comprise between 2.5 and 16.8 wt% Si (Armytage et al., 2011), a range that is even larger than the range derived from the Si elemental partitioning data given above (1–11 wt%; Ricolleau et al., 2011).

The role of HPT experiments

HPT experimental metal–silicate systems aim to simulate the elemental and/or isotopic distribution between planetary cores and mantles. HPT experiments on the elemental partitioning behaviour of Si between metal and silicate have shown that Si becomes more siderophile (iron metal-loving) with increasing pressure and temperature, and decreasing oxygen fugacity (e.g. Kilburn & Wood, 1997; Gessmann et al., 2001; Malavergne et al., 2004; Wade & Wood, 2005; Corgne et al., 2009; Tuff et al., 2011).

Experimental studies on Si isotope fractionation between metal and silicate were carried out by Shahar et al. (2009, 2011) at pressures of 1 and 7 GPa, and temperatures between 1800 and 2200°C. Kempl et al. (2013a) did experiments at 9 GPa and ~2150°C. Kempl et al. (2013b) approached the study of Si isotope fractionation processes at high temperature conditions in an industrial-scale experiment by sampling metal and silicate phases from a blast furnace at Tatasteel IJmuiden, the Netherlands, with maximum temperatures reaching 1600°C during sampling. Hin et al. (2014) performed experiments between 0.5 and 1 GPa pressure, and a temperature range between 1450 and 1750°C.

Here, we review the materials and methods used in these experimental studies, and extend the experimental database by presenting results of metal–silicate Si isotope fractionation experiments done at pressures of 9, 16 and 25 GPa and temperatures between 2150 and 2300°C. We assess to what extent the pressure–temperature effects on Si isotope fractionation can be quantified by combining all available experimental data. Finally, we discuss the implications of our findings for the use of Si isotopic data to constrain core formation in the Earth and other terrestrial planets.

Materials and methods: previously published work

High-pressure experimental methods

High-pressure experiments on Si isotope fractionation have been performed in two different types of apparatus: piston-cylinder presses and multi-anvil presses. A piston-cylinder is a high-pressure apparatus in which several cubic millimetres of sample can be subjected to pressures of up to 4 GPa and temperatures of over 2000°C. The piston-cylinder was developed by Boyd & England (1960), initially to investigate thermodynamic phase-equilibria under HPT conditions. Meanwhile a large variety of piston-cylinders exists, all with very similar operational principles: a sample in a noble metal capsule is inserted into a cylindrical assembly (Fig. 5), which consists mainly of insulating ceramic material, a conducting graphite oven and a thermocouple. The assembly is inserted in the centre of a cylindrically shaped, water-cooled pressure plate. Pressure is applied hydraulically to a piston, which compresses the whole assembly against a top-fixed metal plate (an example is shown in Fig. 6). Temperature is controlled by resistive heating of the graphite furnace. Oxygen fugacity can be controlled by surrounding sample materials with buffer materials. In order to study Si isotope fractionation between metal and silicate, piston-cylinder experiments were run between 0.54 and 1 GPa pressure and in a temperature range between 1450 and 1800°C by Shahar et al. (2009, 2011) and Hin et al. (2014). The latter study used a rotating piston-cylinder apparatus (Schmidt et al., 2006) that enabled improved density separation of metal and silicate phases.

Fig. 5. Sample preparation for a piston-cylinder assembly applied in the quick-press piston-cylinder at VU University Amsterdam. A, B. Assembly preparation with white Al₂O₃ insulation material containing the thermocouple, a corundum disc, the welded Pt capsule with sample material, another Al₂O₃ cylinder hosting the sample capsule and the graphite oven surrounded by talc-pyrex glass; C. The sample assembly is put together and set-up on the piston with an insulation paper (light blue). A thermocouple is located close to the sample; D. The assembly is ready for the experiment and inserted into the piston-cylinder, where pressure is applied from the bottom.

Fig. 6. The quick-press piston-cylinder (Depth of the Earth Department type) at the HPT laboratories of VU University Amsterdam. For calibration and set-up see, for example, Rai et al. (2013).

Pressures above 4 GPa can be reached in a multi-anvil press (e.g. Walker, 1990), in which smaller samples are subjected to higher loads (Fig. 7A). Again samples can be inserted in a noble-metal capsule, which is commonly cold-welded by the pressure of the multi-anvil press. An example of sample preparation is shown in Fig. 7B. Metal–silicate Si isotope fractionation experiments in multi-anvil presses were previously run at pressures of 7 and 9 GPa and between 2000 and 2200°C by Shahar et al. (2011) and Kempl et al. (2013a).

Fig. 7. In a multi-anvil press pressure is also applied hydraulically. A. Sets of first- and second-stage anvils surround the sample assembly so pressure is distributed equally from all sides (http://www.geopetro.ethz.ch/facilities/experimental/multi_anvil); B. The assembly is located in the centre of an octahedron together with a thermocouple. The octahedron is placed between eight tungsten--carbide cubes (first-stage anvils). Paper and tape are used for insulation to ensure constant and controlled heating (photograph by BGI Bayreuth).

Low-pressure experimental methods

Kempl et al. (2013b) used an industrial-scale blast furnace to study Si isotopic behaviour during metal–silicate segregation at low pressure. Industrial-scale hot-metal alloy-producing blast furnaces are used for metal–silicate segregation as a first-step process during steel making. Blast furnaces reach a height of several tens of metres and have a diameter >10 m at their widest point. They are loaded with a burden consisting of natural iron ores (commonly banded iron formations), de-volatised coal, and sinter and pellet materials that are industrially pre-enriched in iron silicates. By controlling oxygen fugacity and temperature in the belly of a blast furnace, hot iron metal is segregated from iron ore, sinter and pellets at high-temperature conditions, and oxygen fugacities close to the iron–wuestite (IW) buffer (Eugster & Wones, 1962).

Kempl et al. (2013b) obtained coexisting metal and silicate samples produced in a blast furnace at Tatasteel IJmuiden, the Netherlands. After the metal was segregated from the iron ore, both hot metal and silicate slag were tapped and could be sampled for investigation after quenching. The temperatures of these sample sets ranged between 1400 and 1600°C during sampling, whereas oxygen fugacities were close to the IW buffer. In the belly of the blast furnace temperatures were likely higher but can only be estimated to range between 1500 and 2400°C.

Starting materials and compositions

A compilation of starting materials, the nature of the samples and experimental conditions is given in Table 1.

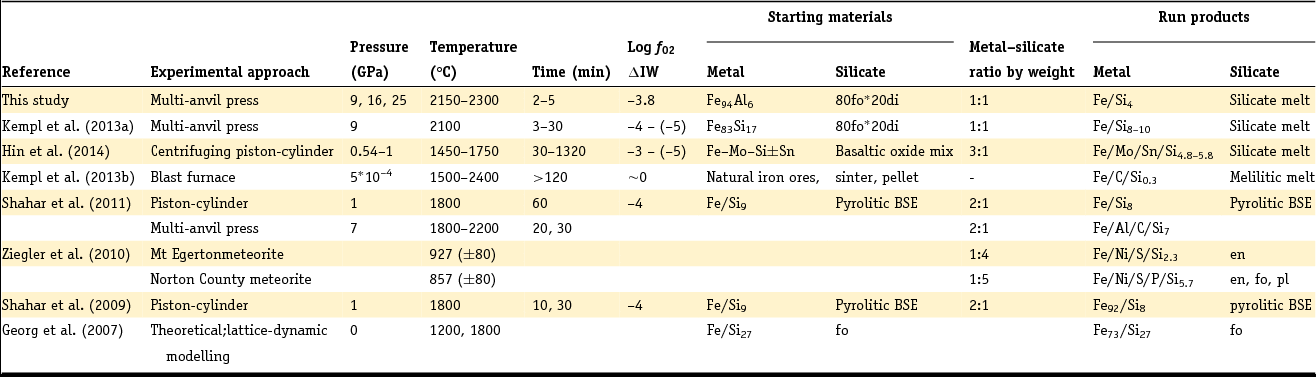
Table 1. Overview of pressure and temperature ranges of samples reviewed in this work

en, enstatite; fo, forsterite; pl, plagioclase; di, diopside.

The Si and Al element concentrations in the metals are given in weight percent. Exact elemental compositions can be found in the respective references.

Shahar et al. (2009, 2011) used experiments containing iron metal with 9 wt% Si and an oxide mixture simulating a BSE composition. The metal phase in their run products typically contained ~8 wt% Si (Shahar et al., 2009). The silicate run product was partially molten, containing both solid olivine grains and quenched melt (Shahar et al., 2011). In both Shahar et al. study an Si isotope spike was added to the silicate starting material (Shahar et al., 2008) in order to track temporal changes in Si isotope fractionation and assess when isotopic equilibrium was reached. The experimental run duration was up to 60 minutes.

Ziegler et al. (2010) investigated the Si isotope fractionation between metal and silicate in two aubrite meteorites that contain Si-bearing metal phases. The silicate composition is given by mineral abbreviations in Table 1. In Ziegler et al. (2010) a detailed explanation of the chemical composition of the metal and silicate phases of the meteorites is given.

In the blast furnace study (Kempl et al., 2013b) coexisting hot-metal alloy and silicate glasses of a melilitic composition were sampled. The hot-metal alloy commonly contained 0.3–0.5 wt% Si, while the silicate contained SiO₂ concentrations between 33.7 and 35.1 wt%.

Hin et al. (2014) made use of different basaltic oxide mixtures combined with either Sn-rich or Sn-free Fe+Si+Mo powder. Sn and Mo were added to lower the melting point of the metal and to enable complete melting at given experimental pressures (Table 1). Each experiment contained about 75 wt% metal powder and 25% silicate. Experimental run times were 30, 90, 240 and 1320 minutes. The run products in Hin et al. (2014) were completely molten and consisted of a silicate melt and a metal alloy bearing between 4.7 and 5.8 wt% Si.

Kempl et al. (2013a) performed a time series at 9 GPa and 2100°C in which the silicate consisted of 80 wt% forsterite (fo) and 20 wt% diopside (di) prepared from the major element oxides SiO₂, MgO and CaCO₃. The metal starting material was a Si-bearing metal alloy with 17 wt% silicon. With increasing experimental runtime this metal Si concentration decreased to 10.0 and 8.8 wt% Si after 13 and 30 minutes, respectively. The SiO₂ concentration in the silicate run products varied between 43.1 and 46.2 wt% (Kempl et al., 2013a). The detailed experimental conditions of all sample sets considered in this work are summarised in Table 2.

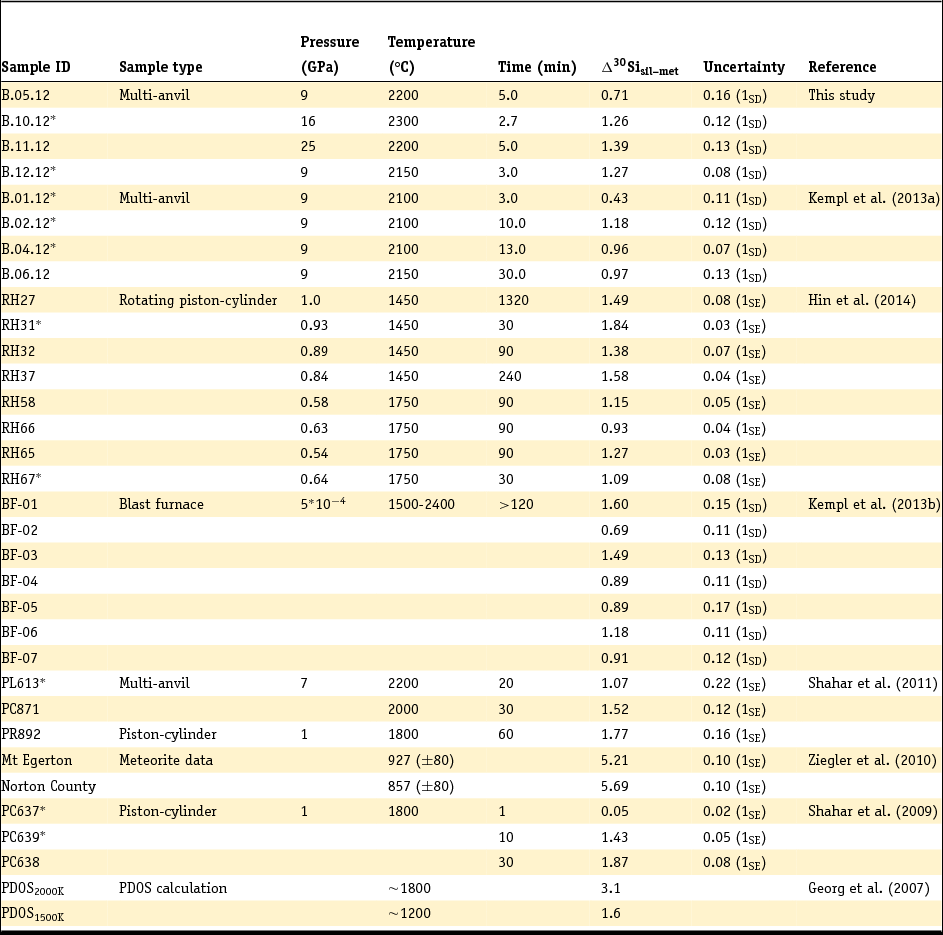
Table 2. Summary of Si metal–silicate isotope mass fractionation (Δ³⁰Si_sil-met) data

*Experiments that authors claim were not of sufficient length to yield full equilibration.

SD, standard deviation, SE, standard error.

Due to the different ways of determining and reporting the analytical uncertainties, the error type is given in brackets.

Si isotope analyses

Silicon has three naturally occurring stable isotopes, ²⁸Si, ²⁹Si and ³⁰Si. Their relative abundances are commonly measured using MC-ICPMS techniques. By using multiple detector systems several isotopes can be measured simultaneously (Fig. 8A). The flat-top intensity peaks enable precise isotope analyses (Fig. 8B). Si isotope variations for Si are, as for other stable isotope systems, reported in the common δ notation, in which the less common isotopes ²⁹Si and ³⁰Si are used to form the isotopic ratios over ²⁸Si. The delta notations for δ³⁰Si (δ³⁰Si = [((³⁰Si/²⁸Si_sample)/(³⁰Si/²⁸Si_standard)) – 1] × 1000 [‰]) and δ²⁹Si (δ²⁹Si = [((²⁹Si/²⁸Si_sample)/(²⁹Si/²⁸Si_standard)) – 1] × 1000 [‰]) are expressed in per mille deviation of a sample relative to a standard. The common NIST Si isotope standard is the Californian beach sand RM-8546 (formerly known as NBS-28).

The use of different ionisation techniques complicates direct comparisons between results obtained in different laboratories (e.g. see discussion in Hin et al., 2014). Even when comparing results that were obtained by using the same type of sample ionisation, the recent review by Savage et al. (2014) shows there are issues with the reported accuracy of some of the literature data on the Si isotope compositions. If not using laser ablation for sample ionisation, MC-ICPMS analyses require dissolving the Si-bearing phases and separating Si quantitatively from the other cations in solution. The different studies listed in Tables 1 and 2 use different sample digestion techniques, which were recently reviewed in Savage et al. (2014).

Fig. 8. A. Schematic of beam splitting in a multi-collector ICP-MS. With this technique eight to ten isotopes can be analysed simultaneously, depending on the machine set-up; B. Si has three stable isotopes that are analysed simultaneously on three different Faraday cups. The Si isotope signal is recorded at the centre of the interference-free peak plateau of all three isotopes, in this case at mass 29.975.

One problem faced by the community studying Si isotope fractionation between metal and silicate is the absence of an international Si-bearing metal standard. This could be a major problem, especially as high Fe/Si ratios in dissolved metal phases can lead to major interferences during analyses due to the formation of iron hydroxides (e.g. Fitoussi et al., 2009). If sample digestion and purification procedures work perfectly there should not be any iron in the sample solutions, but it is unclear if optimal purification is always achieved. An inter-laboratory calibration of an Si-bearing metal standard is even more important when comparing data of samples introduced in an MC-ICPMS by laser ablation.

Materials and methods: this study

In the new experiments performed for this study (Table 1), the silicate starting composition consisted of 80 wt% fo and 20 wt% di, as in Kempl et al. (2013a). This silicate composition was chosen because it is completely molten at the experimental target pressure and temperature conditions. Instead of starting the experiment with some Si already in the metallic form, as was done in all previous experiments, we added 6 wt% metallic aluminium powder to pure iron metal powder (Table 1). The strategy here was to reduce the sample to such an extent that oxidised silicon from the silicate starting composition would reduce and partition into the metal phase. The silicate and metal starting materials were mixed mechanically in a metal–silicate 50:50 ratio by weight.

The new experiments were run in the 1200 and 5000 t multi-anvil presses at the Bavarian Geo-Institute in Bayreuth, Germany. These presses are capable of running experiments at pressures up to 25 GPa and temperatures up to 3000°C. The pressure in the experiments was 9, 16 or 25 GPa at temperatures of 2150–2300°C. We used capsules of MgO single crystals to avoid melting of a noble metal capsule, iron loss to the capsule material and noble metal contamination of our samples.

The chemical composition of the experimental sample charges was analysed by an electron probe microanalyser. The sample-containing part of the experimental assembly was embedded in epoxy after the experiment and polished down to the point of sample exposure. Fine polishing to a finish of less than 1 μm was done using diamond paste (not silicon carbide) to avoid Si contamination.

Major element analyses of the experiments were performed on carbon-coated samples using a JEOL JXA-8800M electron probe at VU University Amsterdam, the Netherlands. Analyses were carried out by applying an acceleration voltage of 15 nA. A 10 μm beam spot size was applied to metals and silicates. Natural fayalite, diopside, corundum and olivine were used as primary standards to quantify Mg, Ca, Si, Al and Fe. Metal analyses were carried out on a FeSi₄ metal alloy. Data were corrected according to the ZAF algorithm (Reed, 2005). The typical accuracy of the analysed element concentrations was on the order of 2% relative.

After electron probe analysis, metal and silicate phases from each experiment were separated mechanically, dissolved and purified. The chemical sample digestion procedure was identical to that reported in Kempl et al. (2013b). Atomic masses 28, 29 and 30 were collected simultaneously on the L4, L1 and C Faraday cups of the ThermoFinnigan Neptune MC-ICPMS at VU University Amsterdam, the Netherlands. The sample introduction system consisted of a Cetac Aridus I desolvating system containing an elemental Scientific PFA microcentric Aspire nebuliser system (dry plasma mode). A mass resolution of about R_Power = 4300 in high-resolution mode and of R_Power = 2500 in medium resolution mode were sufficient (Van den Boorn et al., 2006) to resolve all Si isotopes from common polyatomic interferences. Secondary Si isotope standards included the Hawaiian basalt BHVO-2 and an in-house calibrated Si single crystal (Kempl, 2013).

Results

Literature data

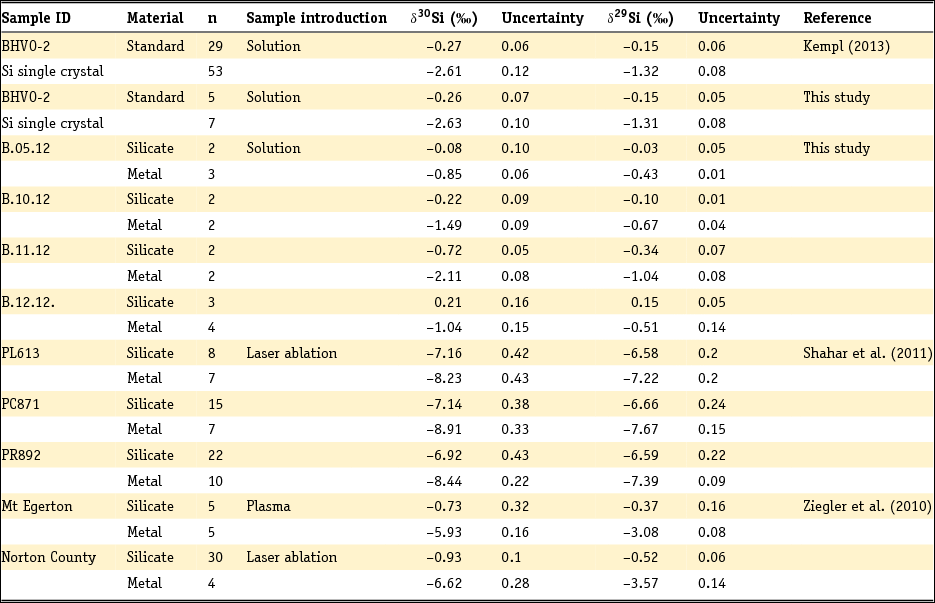
The analysed δ³⁰Si and δ²⁹Si isotope signatures of silicates and coexisting metals from both literature studies and the new experiments are listed in Table 3. The δ³⁰Si isotope signatures of silicates range between –0.72‰ (± 0.05‰; 1_SD) and 0.21‰ (± 0.16‰; 1_SD), while the δ³⁰Si of the metals varies from –2.11‰ (± 0.08‰; 1_SD) to –0.85‰ (± 0.06‰; 1_SD). In addition, we report the average isotope signature of the samples PL613, PC871 and PR892 gathered by Shahar et al. (2011) by laser ablation. Because Ziegler et al. (2010) reports both solution work and laser ablation data, we list the δ³⁰Si and δ²⁹Si signatures of the sample pairs that we chose for this work. The analytical uncertainty in this table is either reported as one standard deviation (1_SD) from the number of analyses (Kempl, 2013, this study; Shahar et al., 2011) or as one standard error (1_SE) from the number of analyses (Ziegler et al., 2010).

Table 3. Si isotope signatures of metals and silicates from HPT experiments plus the average Si isotope signatures from Shahar et al. (2011) and the two datasets from Ziegler et al. (2010)

n, total number of analyses per sample material.

For this study and the data of Shahar et al. (2011) uncertainties are one external standard deviation from the number of analyses. Ziegler et al. (2010) uses one external standard error of the number of analyses.

The isotope fractionation between metal and silicate, Δ³⁰Si_sil-met, is reported and summarised in Table 2. The silicate-metal isotope fractionation of this data collection varies from 0.05‰ (± 0.02‰; 1_SE) for a 1-minute piston-cylinder experiment by Shahar et al. (2009) at 1800°C and 1 GPa up to 5.69‰ (± 0.10‰; 1_SE) and 5.21‰ (± 0.10‰; 1_SE) in the natural samples of Ziegler et al. (2010) equilibrated in solid state over a couple of thousand years between ~850 and ~930°C. The analytical uncertainty in Table 2 is reported in terms of standard deviation or standard error, following the reporting in the individual studies.

This study

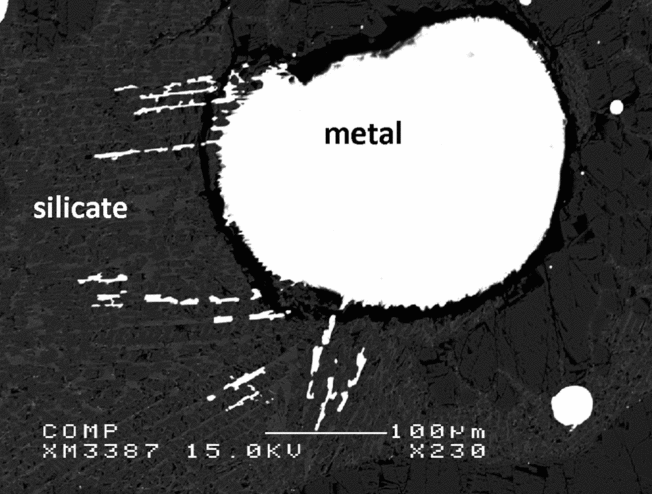
Fig. 9 shows a typical back-scattered electron image of the experimental run products. Both the silicate and metal phases melted completely during the experiments, and the metal phases all coalesced to segregate in spherical blebs that were easy to identify and easy to segregate from the silicate in preparation for dissolution.

Fig. 9. Secondary electron image of experiment B.12.12. The quench texture in the silicate illustrates clearly that the silicate was completely molten at the experimental target conditions. The rounded shape of the metal indicates complete melting and merging of the metal at one ending of the capsule, after the starting materials were mixed mechanically in a metal–silicate 50:50 ratio by weight.

Electron probe analyses show that after the experiments at 9, 16 and 25 GPa, no measurable Al is left in the metal phase, it has all oxidised. The Si concentration in the metals varies between 3.5 and 4.1 wt%, depending on the experimental run time. The synthesised silicate melts contain SiO₂ concentrations between 37.7 and 43.9 wt%.

Standard data, the BHVO-2 basalt standard and the in-house Si single crystal standard were in good agreement with previously analysed data by Abraham et al. (2008), the compilations by Savage et al. (2014) and our own previously published data (Kempl, 2013).

Table 3 shows that the δ³⁰Si of the silicate phases in the new experiments ranges between –0.72 ± 0.05‰ (1_SD) and 0.21 ± 0.16‰ (1_SD). Metals are depleted in the heavier Si isotopes compared to the silicates in each experiment, with δ³⁰Si ranging between –0.85 ± 0.06‰ (1_SD) and –2.11 ± 0.08‰ (1_SD). Δ³⁰Si_sil-met data for the new experiments (Table 2) vary in a narrow range between 0.71 ± 0.16‰ (1_SD) and 1.39 ± 0.13‰ (1_SD). This range is within the total range of metal–silicate Si isotope fractionation data reported to date (Table 2) and appears to be consistent with equilibrated high-pressure samples from previous studies (Shahar et al., 2009, 2011; Kempl et al., 2013a; Hin et al., 2014).

Three-isotope space for Si isotopes

Theoretical calculations predicted that Si isotope fractionation is driven by the different chemical bonding environment of silicon. This assumption implies that a stiffer bonded phase, such as given in silicates, would concentrate the heavier Si isotopes, relative to a weaker bonded phase, such as occurs in metals (Georg et al., 2007; Schauble et al., 2007).

Figs 10A–D show the most recent data summary in the three-isotope space of Si from this study (Ziegler et al., 2010; Shahar et al., 2011; Kempl et al., 2013a,b; Hin et al., 2014). In all cases, silicates concentrate the heavier isotope fraction, metals the lighter fraction. This is consistent with the predictions of Georg et al. (2007) and Schauble et al. (2007). Consistent with mass balance considerations, the silicates provide an infinite Si isotope reservoir and do not show a wide scatter in Si isotopic composition, whereas the metals, which contain a much smaller fraction of the metal–silicate system Si budget, scatter over a wider range in order to equilibrate.

Fig. 10. Three-isotope diagrams of investigated metal–silicate Si isotope fractionation. A. Experimental HT and HPT data of Kempl (2013) and Kempl et al. (2013); B. Experimental HPT data of Hin et al. (2014); C. Si isotope fractionation of two differentiated stone-iron meteorites (Ziegler et al., 2010); D. Experimental HPT data of Shahar et al. (2011). Data in A, B and C are plotted on the equilibrium fractionation line (dark) and kinetic fractionation line (light grey) for Si isotopes. Data in D are plotted on a secondary fractionation line due to the application of an isotope spike technique to the three-isotope method in the experiments. In all experiments silicates provide the silicon reservoir and do not show a large scattering while incorporating the heavy Si isotope fraction. The metals concentrate on the light isotopes and show a large range of scattering due to isotope equilibration.

Discussion

Si isotope fractionation between metal and silicate (Δ³⁰Si_sil-met)

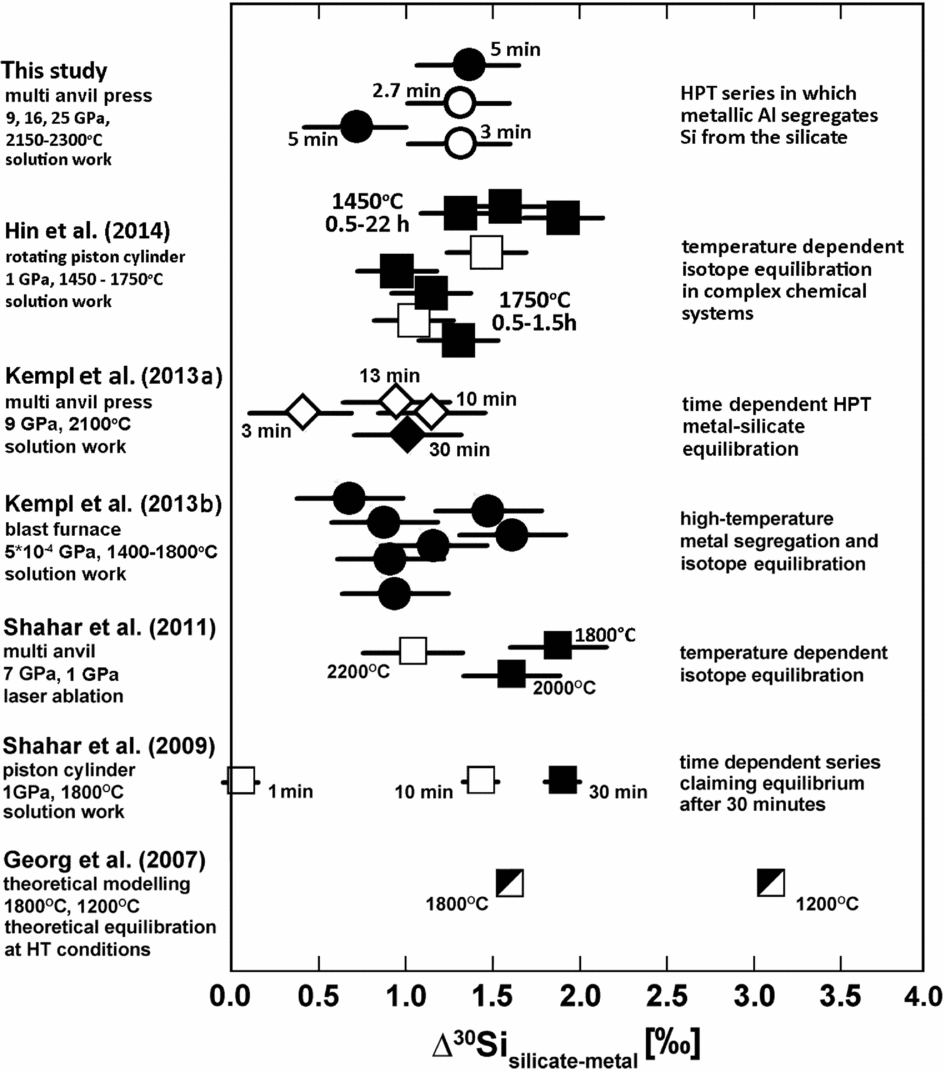
In this study we present the results of metal–silicate partitioning experiments performed at pressures between 9 and 25 GPa and temperatures between 2150 and 2300°C. These are the highest experimental pressures applied in studies of Si isotope fractionation between metal and silicate. A comparison between these high-pressure data and existing lower-pressure data in terms of Δ³⁰Si_sil-met is shown in Fig. 11.

Fig. 11. Compilation of existing data for isotopic mass fractionation between metal and silicate; the sign of all data is positive. The variation of the data is still difficult to constrain.

Whether or not chemical and isotopic equilibrium was reached in the experiments is of primary concern. The experimental run time required for Si isotopic equilibration is still a matter of debate. Hin et al. (2014) showed that Si isotopic equilibrium is reached between 1.5 and 4 hours depending on the experimental temperature of 1750 or 1450°C, respectively, at pressures between 0.54 and 1 GPa in completely molten experiments. Shahar et al. (2011) suggest that isotope equilibration between metal and silicate is reached after 30 minutes at 1 GPa and 1800°C in experiments in which the silicate was only partially molten. In Kempl et al. (2013a) Si metal–silicate isotope fractionation is identical within an acceptable error limit for experiments lasting 13 and 30 minutes at 9 GPa and 2100°C, whereas fractionation differs for shorter run durations. In the Kempl et al. (2013a) experiments, both silicate and metal phases were fully molten.

Although our new HPT experiments were run for relatively short times between 2.7 and 5 minutes, they reached Δ³⁰Si_sil-met values that are consistent with previous high-pressure data run for significantly longer times (e.g. Hin et al., 2014; Kempl et al., 2013a). We have two explanations for this observation:

1. (1) At the very high temperatures of these experiments (>2150°C), at which metal and silicate were both molten, isotopic equilibrium can be reached much faster than at the lower temperatures used in Shahar et al. (2011) and Hin et al. (2014).

2. (2) Because of the aluminium metal powder added to the iron metal starting material, we induced a speed-up of the chemical reaction for silicon to segregate from silicate and to partition into the metal compared to the 9 GPa experiments of Kempl et al. (2013a). The direction of this reaction is opposite to the reaction occurring in earlier experimental studies in which the iron metal initially always contained a large amount of Si. Although the final equilibrated Si isotopic distribution should be independent of the reaction direction, the time it takes to reach this equilibrium could well differ.

Temperature dependence of Δ³⁰Si_sil-met

As is the case for any isotopic fractionation process, the Si isotopic fractionation between metal and silicate is dependent on temperature, with higher temperatures leading to values for Δ³⁰Si_sil-met closer to zero. In Figs 12A–C we compare the temperature-dependent isotope fractionation between metal and silicate derived from Shahar et al. (2009, 2011), Ziegler et al. (2010), Hin et al. (2014) and Kempl et al. (2013a,b), exclusively using their own data points.

Fig. 12. Comparison of the temperature-dependent Si isotope fractionation between metal and silicate from different experimental studies. A. Time-dependent studies in multi-anvil and piston-cylinder experiments (filled markers are equilibrated; empty markers are short-time experiments); B. Short-time experiments at HPT conditions (9, 16 and 25 GPa) with a maximum run-time of 5 minutes scatter within error in the investigated field of equilibration. Experimental equilibration time scales are still a matter of debate; C. Blast furnace data had more than 120 minutes to equilibrate in the belly of the furnace. The occurrence of an SiC gaseous phase causes a dynamic equilibrium to occur and influences the isotope fractionation such that the majority of the data do not plot in the recent field of equilibrium isotope fractionation.

In Fig. 12A the temperature dependences previously obtained from experiments at ~1, 7 and 9 GPa (Shahar et al., 2009, 2011; Hin et al., 2014; Kempl et al., 2013a) are compared with each other. The data at 1 and 7 GPa of Shahar et al. (2009, 2011) show the largest isotope fractionation between metal and silicate, with values that are in good agreement with the natural sample data of the Mt Egerton and Norton County meteorites (Ziegler et al., 2010).

In contrast, the experimental data of Hin et al. (2014) obtained between 0.54 and 1 GPa (Table 2) result in the smallest temperature dependence (Fig. 12A). Our own data previously gathered at 9 GPa and 2100°C (Kempl et al., 2013a) result in a temperature dependence that lies between the dependencies derived from the Shahar et al. (2011) and Hin et al. (2014) experiments (Fig. 12A).

It is still matter of debate what is causing these apparent differences in temperature dependencies. We note that Shahar's silicate sample aliquots were partially molten (as shown in Shahar et al., 2011), consisting of mixtures of olivine grains and a silicate melt. A significant analytical isotope fractionation between silicate crystal and silicate melt was not observed by Shahar et al. (2011). However, both analytical work on larger, natural silicate samples and theoretical calculations of major element isotope fractionation have shown that isotope fractionation among silicate minerals does occur, and can reach several per mille variations depending on the crystalline structures and temperature of equilibration (e.g. Meheut et al., 2007, 2009; Polyakov, 2009; Huang et al., 2010, 2013). Recently, Meheut & Schauble (2014) and Huang et al. (2014) theoretically calculated the silicon isotope fractionation between different silicate phases focusing on the role of the Si and Si–O bonding environments.

Huang et al. (2014) investigated the expected Si isotope fractionation between mantle minerals at HPT conditions up to 25 GPa and 3000K theoretically. They show that silicate–silicate isotope fractionation decreases with increasing temperature and suggest that at the HPT conditions of the Shahar et al. (2011) experiments Si isotope fractionation cannot be resolved analytically at present: the external analytical error on the MC-ICPMS is larger than the predicted isotope fractionation between two (or more) different silicates. We note that a small olivine-silicate melt fractionation of Si isotopes in the Shahar et al. (2011) experiments could provide an explanation for the relatively large external standard deviations in Shahar et al. (2011)’s silicates calculated in Table 3 from their laser-ablation analyses. Although a distinct difference between olivine and melt cannot be observed, the overall analytical uncertainty in the silicate Si isotope measurements reaches more than 0.2‰.

In contrast, the HPT experiments of Hin et al. (2014) and Kempl et al. (2013a) that are equilibrated and considered in Fig. 12A were completely molten, but have significantly different experimental target conditions in terms of pressure and temperature.

Fig. 12B shows the result of the experiments performed in this study, in the pressure range of 9–25 GPa. Overall, the new experimental data are consistent with the range of temperature dependencies previously suggested. Three data points, including the experiments at 16 and 25 GPa, plot on the temperature dependence derived by Shahar et al. (2009), whereas the experiment at 9 GPa with an experimental duration of 5 minutes plots on the temperature dependence based on the experiments by Hin et al. (2014). There is no clear trend in Δ³⁰Si_sil-met as a function of either temperature or run duration in these new experiments. Fig. 12B supports our hypothesis that despite the short run durations involved, our new experiments are consistent with full isotopic equilibration of Si between metal and silicate. This unexpected result suggests that starting with an Si-free metal in these experiments leads to faster equilibration than starting with an Si-rich metal. Finally, we note that the data in Fig. 12B suggest that the pressure effect on Si isotope fractionation between metal and silicate is minor, at least up to pressures of 25 GPa. If it were large a clear deviation of the 16 and 25 GPa experimental data should have been observed.

Fig. 12C shows data that were obtained from sample sets of the industrial blast furnace (Kempl et al., 2013b). The majority of these data plot below the analysed temperature dependence of Hin et al. (2014). Because of the dynamic equilibrium in the SiO₂–SiC–SiO–Si cycle within the blast furnace during steel making (Kempl et al., 2013b), the isotope fractionation between metal and silicate of these samples should be viewed critically. In addition, the error of the temperature of equilibration of these experiments is relatively large due to the imprecise temperature estimation during steel making.

It is important to note that regardless of which of the temperature dependencies shown in Fig. 12 is most applicable, the differences in Δ³⁰Si_sil-met shown in Fig. 11 cannot only be explained by differences in temperature. Correcting all data to a common temperature still leads to major differences in Δ³⁰Si_sil-met between, for example, the experiments at 1 GPa performed by Shahar et al. (2009, 2011) and Hin et al. (2014). These differences are larger than any reasonable analytical uncertainty and must be related to differences in experimental and/or analytical approach or analytical technique, or differences in silicate and/or metal composition. An extensive discussion of the differences between the Shahar et al. (2009, 2011) and Hin et al. (2014) data at 1–7 GPa is provided in Hin et al. (2014) and we will not repeat the pros and cons of those studies here. Suffice to say that the discrepancy between these lower pressure data is not resolved by the addition of the high-pressure data at 9–25 GPa from Kempl et al. (2013a) and this study. In this regard, we reiterate that the absence of an international Si-bearing metal standard makes it hard to compare metal Si isotope data obtained in different laboratories using different analytical techniques.

Conclusions and outlook

We have presented the results of new HPT experiments and combined these with a review of literature data to investigate how the Si isotope fractionation behaviour between metal and silicate varies as a function specifically of experimental run time and temperature. We show that although there is no debate about the sign of fractionation (with silicates isotopically heavier than metals), absolute values for Si isotope fractionation between metal and silicate remain difficult to constrain because the experimental database is sometimes contradictory and certainly incomplete. Si isotopic measurements of metals in particular suffer from the absence of a true inter-laboratory comparison.

We conclude that although individual studies have used their measured metal–silicate fractionation of Si isotopes to derive constraints on the amount of Si in the core of the Earth, there is little agreement between different studies and it remains unclear what causes the disagreement. In order to derive accurate quantitative estimates of the Si content of the core of the Earth or other planets, we suggest that a wide range of additional experiments and analyses will be required.

First, not a single experiment exists that has been analysed by different laboratories. To increase the fidelity of the community's results, large-volume experiments should be performed with the resulting sample charges distributed to several laboratories. This would address any differences in analytical approaches and analytical techniques, in particular with respect to the Si isotopic composition determinations of metal phases. In parallel, an inter-laboratory comparison of a metal Si isotopic standard should be set up.

Second, experiments that assess the extent of Si isotopic fractionation between different silicate phases at high pressure and high temperature are required to assess their effect on the existing metal–silicate fractionation database. Third, single laboratories should explore specifically the effects of pressure, temperature and silicate composition on Si isotope fractionation. Studies published to date, including our own, are based on a very small set of experiments that typically do not enable perfect isolation of individual parameters such as temperature or pressure on fractionation.