1. Introduction
Members of Parliament (MPs) must consider hundreds of bills and motions on a wide variety of issues. Most of these bills are drafted by the cabinet and shepherded by party leaders, but MPs may, under certain circumstances, introduce their own bills and motions through private members’ bills (PMB). In some countries with Westminster systems, such as Canada, the opportunity to introduce PMBs is assigned by lottery at the start of each parliamentary session. Historically, MPs have used PMBs to raise issues that the government was not addressing. For example, in 2001, Svend Robinson, the NDP representative for Burnaby and the first openly gay politician in Parliament, introduced a PMB to legalize same-sex marriage. The bill failed, but it nevertheless drew public attention to an issue that many politicians were inclined to ignore. Four years later, same-sex marriage became legal in Canada. PMBs also provide MPs an opportunity to address constituents’ concerns. In 2007, the House of Commons passed Bill C-288, the Kyoto Protocol Implementation Act, by a substantial majority. Introduced by Pablo Rodriguez of the opposition Liberal Party in May 2006, the bill urged the Conservative government to meet climate change targets set by the Kyoto Protocol, an agreement Canada signed under a previous Liberal government. Supported by all opposition parties and 63% of Canadians at the time (Laghi, Reference Laghi2007), this bill was notable not only because PMBs rarely become law, but also because it directly contradicted the government’s stated policy of not adhering to the Kyoto targets. This event highlighted that MPs can use PMBs not just to challenge government policies but also to potentially enact legislation that influences or pressures the government on significant issues.
The passage of a PMB into law often garners considerable attention from the MP who introduced the bill. The adoption of gender-neutral language in the national anthem occurred due to the passage of a PMB introduced by Mauril Bélanger, an MP who attracted national news coverage. MPs actively communicate their proposals to constituents. During the 40th Parliament, more than 70% of MPs who offered PMBs advertised their proposals on their personal websites (Blidook, Reference Blidook2012). In the UK, participation in Question Time has evolved significantly; historically, MPs seldom engaged, but they now pose the maximum number of allowable questions. Norton Reference Norton(1994) points to a survey indicating that 90% of MPs stated their primary reason for asking questions was to inform ministers of constituents’ concerns. Additionally, over 80% reported that they forwarded the answers to their questions to local press outlets. In the Canadian context, despite the prevalence of strong party discipline, approximately 5 to 8 percent of voters indicate that their electoral decisions are influenced by individual candidate preferences rather than party affiliation (Blais et al., Reference Blais, Gidengil, Dobrzynska, Nevitte and Adeau2018; Sevi et al., Reference Sevi, Aviña and Blais2022). Consequently, although not to the same degree as their American counterparts, Canadian MPs are attuned to opportunities to win the “personal vote” (Cain et al., Reference Cain, Ferejohn and Fiorina1987; Norton, Reference Norton1993; Studlar and McAllister, Reference Studlar and McAllister1996; Docherty, Reference Docherty1997; Solvak, Reference Solvak2013; Sevi Reference Sevi2023, Reference Sevi2025). Activities that enhance an MP’s vote share typically involve actions that individual MPs can personally claim, which Mayhew Reference Mayhew(2004) classifies as advertising, position-taking, and credit-claiming. However, opportunities for such activities within Parliament are limited, with PMBs being an important exception.
Research on PMBs in parliamentary systems is crucial given the growing perception that these systems have become increasingly partisan, often reflecting party agendas rather than genuine private member initiatives. This dynamic aligns with the broader concept of dyadic representation, which has received limited attention in parliamentary systems where party discipline is pronounced (Huber, Reference Huber1996; Diermeier and Feddersen, Reference Diermeier and Feddersen1998). In Canada, the fusion of the legislature and the executive amplifies party cohesiveness, restricting MPs’ ability to act independently, particularly as party leaders wield significant influence over MPs’ career trajectories (Docherty, Reference Docherty1997; Savoie, Reference Savoie1999; Carty et al., Reference Carty, Cross, Young and Alper2000; Sevi Reference Sevi, Yoshinaka and Blais2018). Polling data reveal that constituents often feel their representatives do not adequately advocate for their interests (Anderson and Goodyear-Grant, Reference Anderson and Goodyear-Grant2005; Dassonneville et al., Reference Dassonneville, Blais, Sevi and Daoust2021). However, previous research suggests that some MPs exhibit a genuine desire to shape policy, motivated by both personal interests and constituent needs (Kornberg, Reference Kornberg1966, Reference Kornberg1967; Clarke and Kornberg, Reference Clarke and Kornberg1992; Docherty, Reference Docherty1997; Blais et al., Reference Blais, Gidengil, Dobrzynska, Nevitte and Adeau2003). The link between legislators’ behavior and the preferences of their constituency shows evidence of constituency representation in the Canadian context within the constraints of a strong party system (Soroka et al., Reference Soroka, Penner and Blidook2009; Blidook, Reference Blidook2012).
Unlike other aspects of Parliamentary business, which are characterized by strict party discipline, PMBs offer greater flexibility. PMBs represent some of the few opportunities, and arguably the most effective, for individual MPs to express their positions on policy matters within the legislature without the party hierarchy dictating their content or placement (Blidook, Reference Blidook2012). Canadian MPs enjoy considerable latitude when crafting their proposals and may vote in ways that deviate from the preferences of party leaders or co-partisans (Cochrane et al., Reference Cochrane, Blidook and Dyck2021). Although PMBs are sometimes decided by party votes, this domain of parliamentary politics nevertheless provides a window into legislative behavior outside strict party control.
Central to the study of coalition building in the absence of strong party control is the concept of reciprocity. Reciprocity is a form of cooperative behavior that facilitates the creation and maintenance of coalitions. For legislators who are already allied in some way, reciprocity may require little effort; for legislators who ordinarily find themselves at odds, reciprocity may require some give-and-take. In the context of the current study, legislative reciprocity culminates in MPs openly supporting each others’ proposals (Milner, Reference Milner1999): MP A seconds or votes in support of MP B’s proposal, and MP B returns the favor by seconding or voting in support of MP A’s proposal. Although those who study politics rarely observe the “agreement” that sets reciprocity in motion, anecdotes conveyed by former legislators often recount instances in which such bargains were struck. More generally, in legislatures “back-scratching” is an expected form of interaction between representatives, and politicians are thought to routinely exchange favors, such as seconding proposals (Gilbertson, Reference Gilbertson1917; Field, Reference Field2014).
Homophily greatly complicates the study of reciprocity, however. MPs who share similar backgrounds and experiences tend to have common goals. Moreover, signaling these shared inclinations is a way to appeal to constituents and interest groups. Thus, even if the strategic logic underlying reciprocity had little motive force for most legislators, it would not be surprising if legislators from the same party or region jointly supported or opposed the same PMBs. Homophily makes it difficult to draw clear causal inferences from observed patterns in which MP A and MP B second and support each other’s proposal.
Relatively few studies of legislative behavior have leveraged random assignment in order to isolate the causal effects of reciprocity. Although scholars have considered the possibility that vote trades might occur when legislators are randomly assigned neighboring offices (Rogowski and Sinclair, Reference Rogowski and Sinclair2012) or adjacent seats in the legislative chamber (Harmon et al., Reference Harmon, Fisman and Kamenica2019), such studies consider social networks rather than exogenously allocated legislative resources that could be precipitate exchanges between legislators. Similarly, the literature that looks at micro-level predictors of co-sponsorship stops short of drawing a causal connection to institutional endowments. For example, Goodliffe et al. Reference Goodliffe, Rothenberg, Sanders and Interactive2005’s study of co-sponsorship behavior in the U.S. Congress reveals that co-sponsorships are more likely between ideologically similar representatives. Burkett and Skvoretz Reference Burkett and Skvoretz(2001)’s investigation of co-sponsorship networks within the U.S. Senate offers suggestive evidence of reciprocity whereby legislators who co-sponsor their colleagues’ measures expect support in return. Important recent work by Fong Reference Fong2023 argues that reciprocity may be more widespread in legislatures than is often assumed. Using a combination of survey experiments and observational evidence from the United States, Fong Reference Fong2023 argues that legislators express an intrinsic motivation to repay favors. Such favors are repaid even to those who are about to leave office, despite the temptation to renege. If true, patterns of legislative behavior that seem to involve reciprocity reflect more than mere homophily; there is truly a causal effect of receiving a favor.
In the present study, we leverage a random lottery in Canada that, at the start of each parliament, assigns the order in which MPs can propose a bill or motion. Because the parliamentary session invariably ends well before all lottery numbers are called, the lottery effectively gives some MPs a strong chance to make proposals, while other MPs’ chances are remote. The question is whether this randomly assigned asset gives rise to any detectable patterns of seconding. When a proposal is introduced in the House for introduction and first reading, the name of the proposer is the sponsor. It is a procedural requirement for the proposal to have one MP to second the bill or motion for it to be formally presented in the House of Commons. Once a bill or motion has been formally introduced and given its first reading, MPs who wish to show support may notify the Clerk of the House in writing, indicating their desire to jointly second the bill or motion. The MP/mover who initially seconded the proposal to formally introduce the bill or motion is not automatically counted among the joint seconders (unless they also jointly second). In this paper, we focus on the individuals who jointly second the proposal, which we will refer to as “seconding” from here on. Seconding refers to the act of supporting a bill or motion introduced by another MP. When an MP seconds a proposal by another MP, it indicates their endorsement and willingness to support the initiative. This collaborative effort is common but far from universal; since 2004, 43 percent of PMBs have attracted at least one second.
One possibility is those holding top priority numbers are keen to second other MPs’ proposals in exchange for votes and seconds in the current parliament.
The Canadian lottery system also provides an opportunity to examine reciprocity over time. Only MPs with the good fortune to make a proposal are eligible to attract seconds from other legislators. If reciprocity is at work, the randomly eligible receivers of seconds in one parliament will be grateful givers of seconds in the current parliament or a future parliament. By tracking seconds over a sequence of parliaments, we leverage an elegant naturally-recurring experiment to shed light on the causal effects of reciprocity, as distinct from factors such as shared ideological convictions that lead to mutual seconds.
Our paper is organized as follows. We begin by describing the Canadian lottery system and the research opportunity that arises for those studying legislative reciprocity. In order to clarify the empirical implications of reciprocity, we offer a brief formal description of the strategic incentives that might lead to an exchange of favors. Next, we describe the data for our study and the statistical model that we will use to assess the effects of lottery number. We then turn to our results, first describing aggregate trends over time in terms of the frequency of seconding and, next, assessing the causal effects of random priority numbers on MPs’ probability of seconding others’ proposals. Examining patterns of seconding over successive parliaments, we find weak evidence that those whose lottery numbers enabled them to receive seconds in one parliament are more likely to extend seconds in the next parliament. Although these patterns may eventually come into sharper focus statistically over time as future parliaments are analyzed, for now it appears that correlated seconding is primarily due to homophily rather than reciprocity.
2. Background: private members’ bills and seconding
PMBs in Australia (Dixon, Reference Dixon2004), Canada (Loewen et al., Reference Loewen, Koop, Settle and Fowler2014; Green and Sevi, Reference Green and Sevi2023), New Zealand (Williams and Indridason, Reference Williams and Indridason2018), and the United Kingdom (Bowler, Reference Bowler2010; Hazell and Reid, Reference Hazell and Reid2018) give MPs an opportunity to make proposals independent of the government or party leaders. In each parliament, hundreds of PMBs are typically proposed. Time is set aside in each session, during which PMBs are given precedence. These PMBs are proposed, debated, and voted on. The opportunity to forward proposals in Canada, New Zealand, and the United Kingdom is decided by a random draw at the beginning of each parliamentary session; all MPs’ names are entered except cabinet ministers and parliamentary secretaries.
Given that there is limited time to deal with PMBs, MPs who draw low numbers are especially well-positioned to present their proposals before the parliamentary session ends. The conventional wisdom is that MPs who propose PMBs can get an electoral boost for pursuing legislation that can be picked up by the media and/or the MPs constituents. In this way, MPs who propose legislation may also raise their profile and popularity. Proposing a bill or motion may allow MPs to signal their commitment to their constituency, thereby improving their standing with voters. Although the actual electoral effects of the lottery appear to be muted (Green and Sevi, Reference Green and Sevi2023), PMBs play an important role in the legislative process. Indeed, there are many examples of PMBs that have passed into law and had a lasting impact. In the UK, “the abolition of slavery, abolition of capital punishment, de-criminalization of homosexuality, the availability of abortion on certain grounds, same-sex marriage” are all matters that were first put forward by PMBs (Hazell and Reid Reference Hazell and Reid2018; p.123). Similarly, in Canada, restricting smoking in federally regulated workplaces and on airplanes, trains, and ships and extending voting rights to Canadian citizens abroad are issues that were first put forward as PMBs.Footnote 1
Reciprocity frequently emerges in the form of informal exchanges, mutual support, and collaborative efforts among legislators (Kirkland and Williams, Reference Kirkland and Williams2014). In Canada, MPs across parties have intensified their lobbying activities to generate the momentum necessary for the passage of their PMBs. A notable example is Bill C-237, introduced in 2015 by New Democratic MP Kennedy Stewart (Burnaby South, BC), which aimed to amend the Canada Elections Act by imposing a financial penalty on parties that presented candidate slates with more than a 10 percent disparity between the number of men and women. In response to this proposal, Liberal MP Mark Gerretsen (Kingston and the Islands, ON) questioned why the bill focused exclusively on gender and did not consider other minority groups. MP Kennedy Stewart replied that “since this is a private member’s bill and not a government bill, I am limited in the scope that I can present in this bill. I thought that gender equity was the most important issue to tackle at this time. I welcome the government’s future efforts to extend equity measures in the House and would be happy to vote for them.”Footnote 2 This exchange highlights the potential importance of coalition-building in the legislative process, illustrating how legislators engage in dialogue and collaboration to advance shared goals.
Under what conditions do legislators second private members’ bills or motions?
Theories of legislative behavior suggest that those who would make proposals seek to build support for their initiatives, and seconding others’ proposals is a way to exchange support. As noted earlier, there are other reasons why an MP might want to jointly second a proposal. The first is that seconding is a relatively costless way for politicians to signal their position to their colleagues or their constituents (Campbell, Reference Campbell1982; Kessler and Krehbiel, Reference Kessler and Krehbiel1996). Several scholars have found that seconding is higher among new legislators, members of the minority party, and legislators who are electorally vulnerable (Campbell, Reference Campbell1982; Wilson and Young, Reference Wilson and Young1997; Koger, Reference Koger2003). Furthermore, jointly seconded PMBs have a significantly higher likelihood of becoming law compared to those sponsored by individual members (Morden, Reference Morden2022).
In the present study, we examine whether there is evidence of reciprocity within and between legislative sessions. To do so, we use the 38th, 39th, 40th, 41st, 42nd, and 43rd parliaments in Canada for a total of six parliaments from 2004 to 2021. Since 2004, the names of all eligible members (non-cabinet members and parliamentary secretaries) in the Canadian House of Commons are randomly chosen by lottery to determine who has the right to introduce PMB or motions. The names of MPs and the order in which they are drawn form the Order of Precedence at the beginning of each Parliament.
A legislator who introduces a bill or motion is its sponsor. Other legislators who jointly support a given bill or motion are its seconders.Footnote 3 Canadian parliamentary records indicate which MPs are sponsors or seconders of all proposals. Whereas focusing on roll call votes gets at the outcome of the legislative process, here we focus on seconding, which reflects alliance formation at an earlier stage (Sinclair and Brady, Reference Sinclair and Brady1987; Whiteman, Reference Whiteman1995).
3. Formalizing reciprocity and its empirical implications
Suppose each MP has a proposal that would be submitted as a PMB if the opportunity were to arise. The utility that an MP derives from this proposal is Up if the PMB passes, Uf if the PMB is proposed but not passed, and U 0 if the session ends before the MP has an opportunity to make a proposal. Suppose that for all MPs, ![]() $U_p \gt U_f \gt U_0$. This preference order implies that MPs gain expected utility when the lottery assigns them a favorable priority number.
$U_p \gt U_f \gt U_0$. This preference order implies that MPs gain expected utility when the lottery assigns them a favorable priority number.
Seconding enters the strategic calculus in the following way. An MP pays some cost c for soliciting a second or some cost s for seconding a proposal made by another MP, but receiving a second increases the probability of passage by some positive amount.Footnote 4 Receiving a second is of little immediate value to MPs with unfavorable lottery numbers because these MPs are unlikely to be able to make a proposal. However, if those with unfavorable lottery numbers imagine that other MPs will reciprocate a second in the future, they may, depending on their discount rate, be willing to pay some cost to second others’ proposals in the near term in order to receive a second at such time when they draw a favorable lottery number. As for those who currently hold favorable lottery numbers, they have a more attractive present value calculation because floor recognition allows them to reap Up or Uf now rather than a discounted return in the future. The present value of receiving a second is also greater than it would be if the second were directed to an uncertain future proposal. All else being equal, they will be more likely than those with unfavorable lottery numbers to solicit seconds and second others’ proposals in an effort to reap Up rather than Uf.
Of course, there is no guarantee that seconding someone else’s proposal will lead them to second one’s own proposal, now or later. This is where norms and expectations about norm compliance come in. If reciprocity norms are routinely enforced via disdain or ostracism, MPs may be justified in expecting reciprocity when they help others. In addition, MPs may sense that they and others are intrinsically motivated to repay favors (Fong, Reference Fong2023). Strategic calculations about how to win floor support in the future by assisting other MPs in the near term may reasonably depend on favors being repaid when prevailing norms are socially enforced and bolstered by MPs’ intrinsic motivations. This confluence of motives may explain why cooperation and exchanges of support have long characterized legislators’ interactions (Matthews, Reference Matthews1959).
4. Identification challenges
To what extent do legislators reciprocate by supporting each other’s proposals? Because who receives seconding from whom reflects unobserved factors such as shared preferences or social backgrounds, we have to be careful to adopt an identification strategy that leverages random assignment.Footnote 5 Our strategy effectively amounts to an “encouragement design” (Eckles et al., Reference Eckles, Kizilcec and Bakshy2016; Paluck et al., Reference Paluck, Shepherd and Aronow2016) whereby MPs whose lottery number affords them the right to propose a bill or motion have a greater incentive to second other bills or motions. Conversely, we expect seconding to be discouraged among politicians whose lottery number makes them unable to propose anything. In other words, rather than use observed seconding by one legislator to predict whether another legislator seconds, we instead examine whether lottery assignments that provide certain legislators with an incentive to court seconds make them more likely to second others’ PMBs.
This agnostic approach, which was preregistered,Footnote 6 may seem unsatisfying to readers familiar with network models that draw inferences from observed correlations in legislators’ behavior across time and between individuals. However, the advantage of our approach is its design-based nature, where causality is assessed by comparing randomly assigned groups. That said, we have made our data and replication files publicly available and encourage other scholars to use them for replication or to apply a network model. If our approach demonstrates that legislators who by chance receive different priority numbers behave differently in terms of the seconds they provide to other legislators’ PMBs, that would be strong evidence that the power to propose sets in motion legislative back-scratching.
5. Data and methods
The data for our study come from several sources. First, the Library of Parliament provides information on the Order of Precedence, whether the Member of Parliament proposed a bill or motion, whether it reached second reading, and whether it passed. The order in which PMBs are considered is determined at the beginning of each new session. At that time, the names of all MPs, excluding cabinet ministers and parliamentary secretaries, are randomly drawn by the Clerk of the Legislative Assembly to establish the order of consideration. MPs are not required to specify the items they intend to introduce at this stage.
To ensure the “List for the Consideration of Private Members’ Business,” which we refer to as the “place on list,” is generated through a random ordering of all eligible MPs in that session, we consulted with the Procedural Clerk of the House of Commons. On rare occasions, MPs choose not to propose a motion or bill when their turn arrives. For example, Michael Chong opted out during the 42nd Parliament despite being 53rd on the list, and Linda Lapointe, who was 26th, also did not proceed. These MPs are still included in our dataset. In Lapointe’s case, her seconders are also included. Although she missed the date for her second reading and was moved to the bottom of the list by the Speaker, we do not alter her original lottery number in the dataset—she remains listed at position 26.
As mentioned previously, once a bill or motion has been formally introduced and given its first reading, MPs who wish to show support notify the Clerk. No more than 20 MPs may jointly second an item under PMB. According to the Procedural Clerk of the House of Commons, the window for seconding a PMB starts after the proposal is introduced and ends before the debate starts at second reading.
Pursuant to Standing Order 86(3), the names of the Members wishing to support the bill will be added to the list of joint seconders on the Order Paper. Once the order for second reading has been proposed to the House, no additional names may be appended. In practice, this means that joint seconders can be added as soon as a bill has been introduced, read a first time, and transferred to the list of “Private Members’ Business—Items Outside the Order of Precedence”, and up until the debate starts at second reading.
Of 1,507 MPs in the dataset, only 27 MPs’ proposals attracted 20 joint seconders. Thus, the extent of truncation of the outcome variable is fairly minor and does not materially affect the results (see Figure 3).
We constructed a seconder dataset that documents each MP who seconded a bill or motion, along with the corresponding session number, bill identifier, and motion identifier. Our analysis encompasses six parliaments during which the lottery system was fully implemented, examining the universe of private members’ proposals from 2004 to 2021. This dataset is then merged with Sevi Reference Sevi(2021)’s data regarding MPs’ backgrounds.
Cabinet members and parliamentary secretaries are excluded from our analysis, as they are ineligible for the lottery.Footnote 7 MPs may propose either a bill or a motion. While bills require substantial time and effort to draft and navigate through the legislative process, they generally bring about more significant policy changes if successful. In contrast, motions are easier to introduce and pass but typically carry less weight, even when approved. Consequently, MPs who prioritize substantive policy change are more likely to propose bills, whereas those focused on public visibility and political positioning tend to favor motions. In this study, we combine both bills and motions, as our primary interest lies in exploring the concept of reciprocity.
We have three dependent variables for the main analysis: 1) “Seconded,” which is a binary variable indicating whether the MP seconded a proposal in the current session; 2) “Given,” which is an integer count variable indicating the number of proposals an MP seconds in the current session; and 3) “Received,” which is an integer count variable indicating the number of proposals an MP receives in the current session (which presupposes that an MP was eligible to make a proposal in the current session).Footnote 8 Our main independent variable is placed on the randomly assigned list. “Place on List” is a continuous variable ranging between 0 and 1 that represents the relative random ordering that each MP is given at the beginning of each Parliament. We also include parliament indicators as covariates because the probability of being a lottery winner varies from one parliament to the next.
In order to describe who seconds whose proposals, we also construct a dyadic version of the data. The dyadic dataset contains one entry for each dyad in each session. For each member of the dyad, we looked up whether that MP supported the other MP using our second dataset (see above). The logic of the dyad dataset may be illustrated by a simple example. Our dyadic dataset includes every possible pairing of MPs within a session. The pairs are ordered with the first MP in the pair being the one who has the lowest (the better) lottery number. Letting A be the first member of the pair and B being the second. There are four possibilities for dyadic support:
(1) A supports B but B does not support A
(2) B supports A but A does not support B
(3) Mutual support
(4) Neither supports the other
For descriptive purposes, we retained each individual member’s party affiliation. In this way, the dyadic dataset allows us to summarize not only the frequency of seconding but also the extent to which they cross party lines.
5.1. Statistical models
Based on our theoretical expectations, reciprocity may be evident at the individual level in the relationship between MPs’ places on the list and their seconding behavior. As discussed above, we expect that MPs who are afforded a favorable place on the list will be more likely to second other MPs’ proposals.Footnote 9
Our analysis of individual-level data (Table 4) consists of fitting six models to the data described above. These models are specified in the following equations.Footnote 10
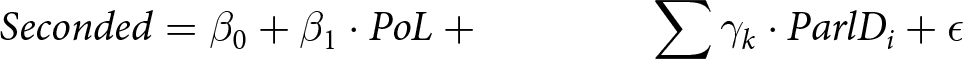 \begin{align*}
Seconded &= \beta_{0} + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Seconded &= \beta_{0} + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}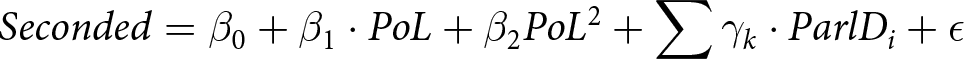 \begin{align*}
Seconded &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Seconded &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*} \begin{align*}
Given &= \beta_0 + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \,\,\quad\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Given &= \beta_0 + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \,\,\quad\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}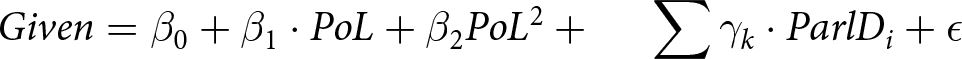 \begin{align*}
Given &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \,\,\quad\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Given &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \,\,\quad\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}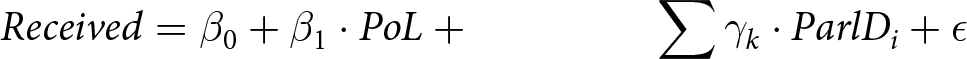 \begin{align*}
Received &= \beta_0 + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \,\,\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Received &= \beta_0 + \beta_1 \cdot PoL + \phantom{\beta_2 PoL^2 +}\ \,\,\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}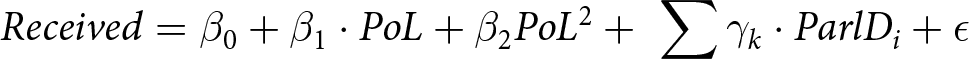 \begin{align*}
Received &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \,\,\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}
\begin{align*}
Received &= \beta_0 + \beta_1 \cdot PoL + \beta_2 PoL^2 + \,\,\sum \gamma_{k} \cdot ParlD_{i} + \epsilon
\end{align*}In these equations, Seconded is the first dependent variable, which indicates whether the MP seconded at least one PMB. Given is the second dependent variable; it indicates the number of proposals an MP seconds in a given session. Received is the third dependent variable, which indicates the number of seconds an MP receives in a given session. The variable PoL is the MP’s place on the list of lottery-generated priority numbers. Finally, ParlDi are dummy variables indicating the ith Parliament. Models 2, 4, and 6 also include a squared component for a place on the list because we expected a non-linear effect of PoL.
6. Results
We begin with some descriptive statistics on the introduction of bills and their seconding over the six parliaments under study. The top panel of Figure 1 plots the number of proposals and seconds between the 38th and 43rd parliaments.Footnote 11 The figure shows that the number of proposals and seconds fluctuate from session to session. However, when we look at the bottom panel, which normalizes the statistics in the top panel by the number of sitting days in each parliament, we see a clearer pattern. Over the period under study, the House of Commons processed approximately one proposal every six to ten sitting days. While there appears to be a slight decreasing trend in the rate at which PMBs are proposed, the rate appears steady in recent years. The rate at which proposals have been seconded, on the other hand, has steadily increased relative to the rate at which proposals have been processed.Footnote 12
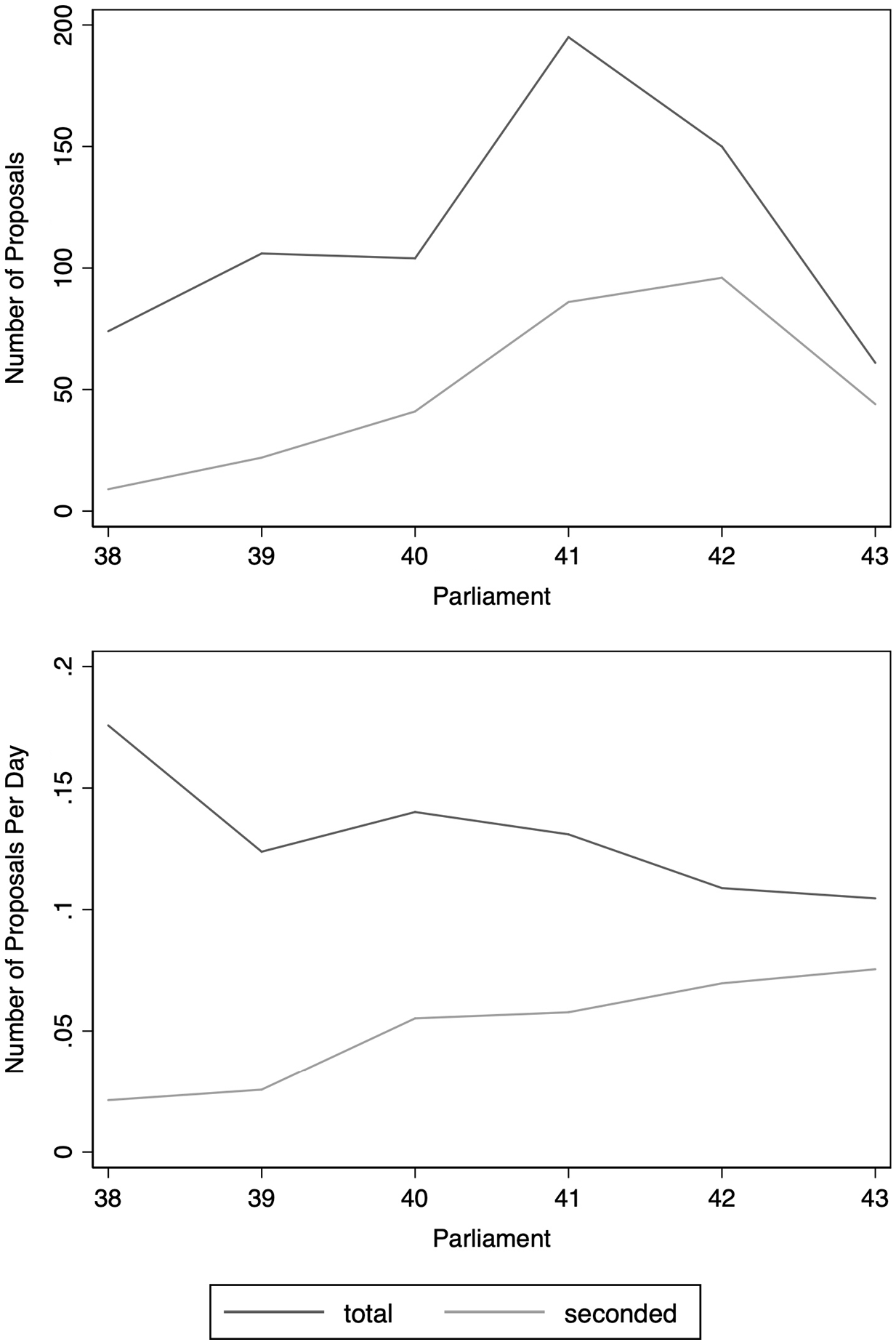
Figure 1. Total Number of Proposals and Seconds in Each Parliament.
Table 1 shows various descriptive statistics about our data. Nearly half (49%) of the MPs in our sample had the power to propose. An overwhelming majority (93%) of MPs who had the power to propose brought a bill or motion to Parliament. Less than half (43%) of these proposals were seconded. Two-fifths (40%) of the MPs seconded at least one proposal. Just over one-third (37%) of the proposals passed. The average number of seconds given by an MP is 1.16 with a standard deviation of 2.4. Finally, the average number of seconds received is 0.91 with a standard deviation of 3.41; supplementary analyses (see Table B.1) suggest that the number of seconds received by a proposal is positively correlated with the probability that it will pass.
Table 1. Descriptive statistics
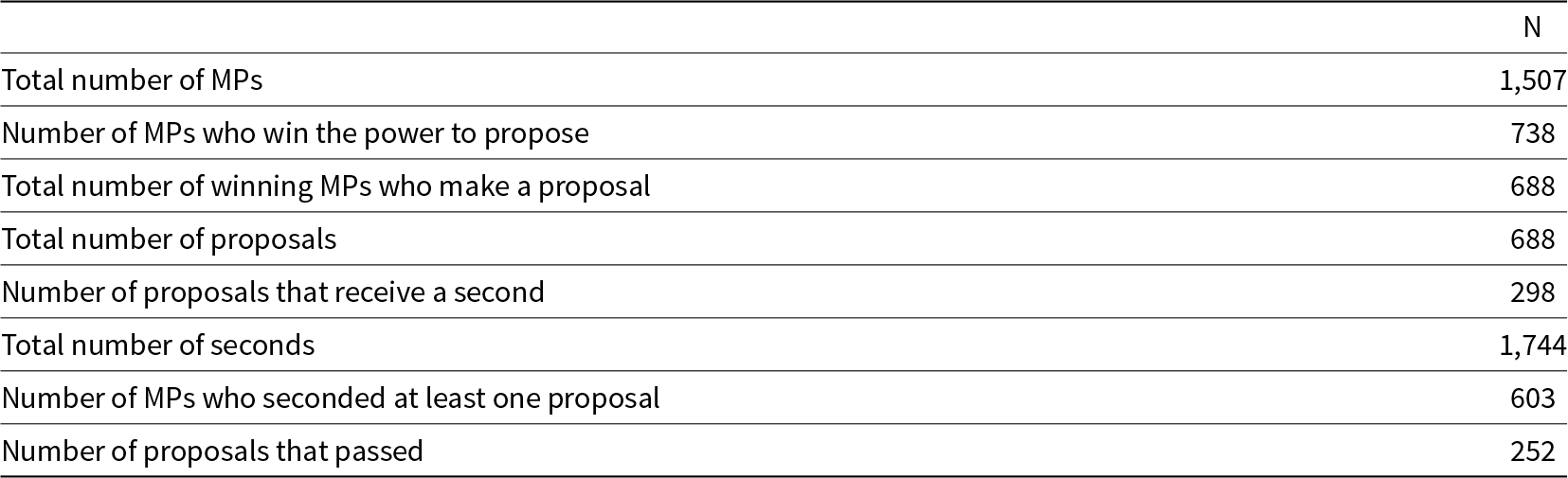
Note: MPs can make at most one proposal.
The dyadic data allow us to describe aggregate patterns of seconding in greater detail. Table 2 shows the distribution of the level of mutual support within dyads where at least one member has the power to propose. The overwhelming majority (99%) of dyads do not support each other’s proposals. There are only 27 cases where both MPs support each other’s proposals. Among 51,679 dyads where both members had the power to propose, exactly one member of the dyad supported the other member’s proposal in 687 cases.
Table 2. Number of seconds among dyads where at least one MP has the power to propose

Note: Entries indicate the number of seconds exchanged per dyad.
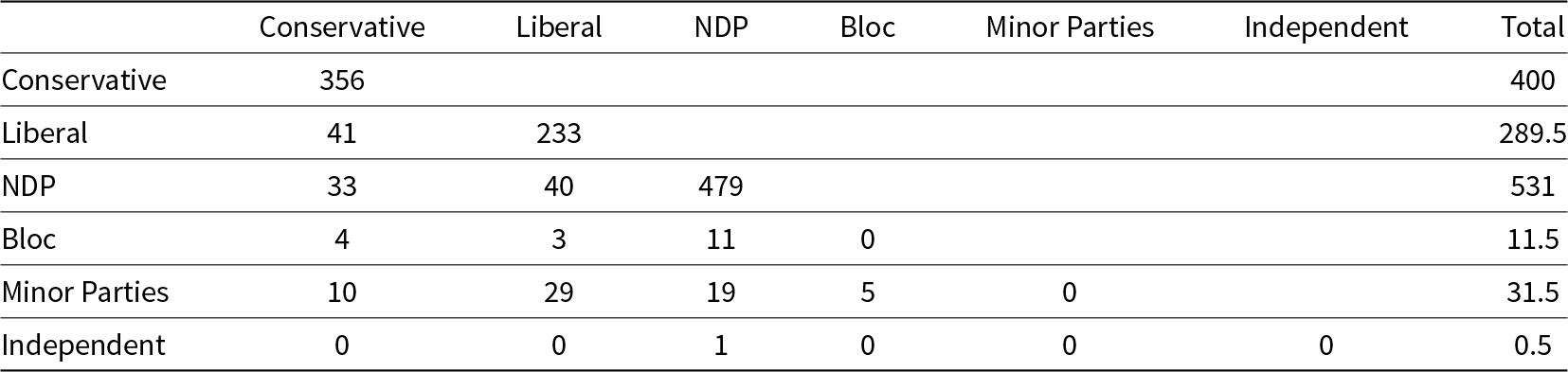
Looking now at seconding within and across party lines, Table 3 shows that, in the aggregate, dyads are more likely to exhibit mutual support when their members share the same party. The data in Table 3 are counts of dyads with at least one second and at least one member has the power to propose. The party totals are weighted. Dyads whose members are of the same party receive a weight of 1 and dyads whose members are of different parties receive a weight of .5. For example, there are 356 dyads where both members are from the Conservative party and at least one of them supports the other’s proposal. Similarly, there are 41 dyads in the dataset where one member is from the Conservative and the other is from the Liberal party and at least one member of the dyad supports the other. An inspection of Table 3 reveals that a very large majority of cases involve dyads with matching party membership, which is consistent with our expectations.
Table 3. Dyadic seconding, by party
Turning now to the contemporaneous causal effects of random lottery endowments, we begin by inspecting the patterns graphically. Figure 2 illustrates the relationship between an MP’s place on the list (horizontal axis) and the number of seconds that each MP gives by parliament (vertical axis). Thus, each dot represents the number of seconds given by the MP who was assigned the corresponding lottery number. For example, in the graph for the 38th Parliament, the point whose y-coordinate is 7 represents MP Bev Desjarlais, from the NDP, whose lottery number was 100 and who seconded 7 proposals. The red line on the plots represents a flexible LOESS regression line to help visually identify seconding patterns. Overall, the relationship between MPs’ place on the list and their seconding behavior is faint and varies from one legislative session to the next. If there is an overall pattern here, it must be extracted from a statistical analysis, as it is not apparent from simple inspection.
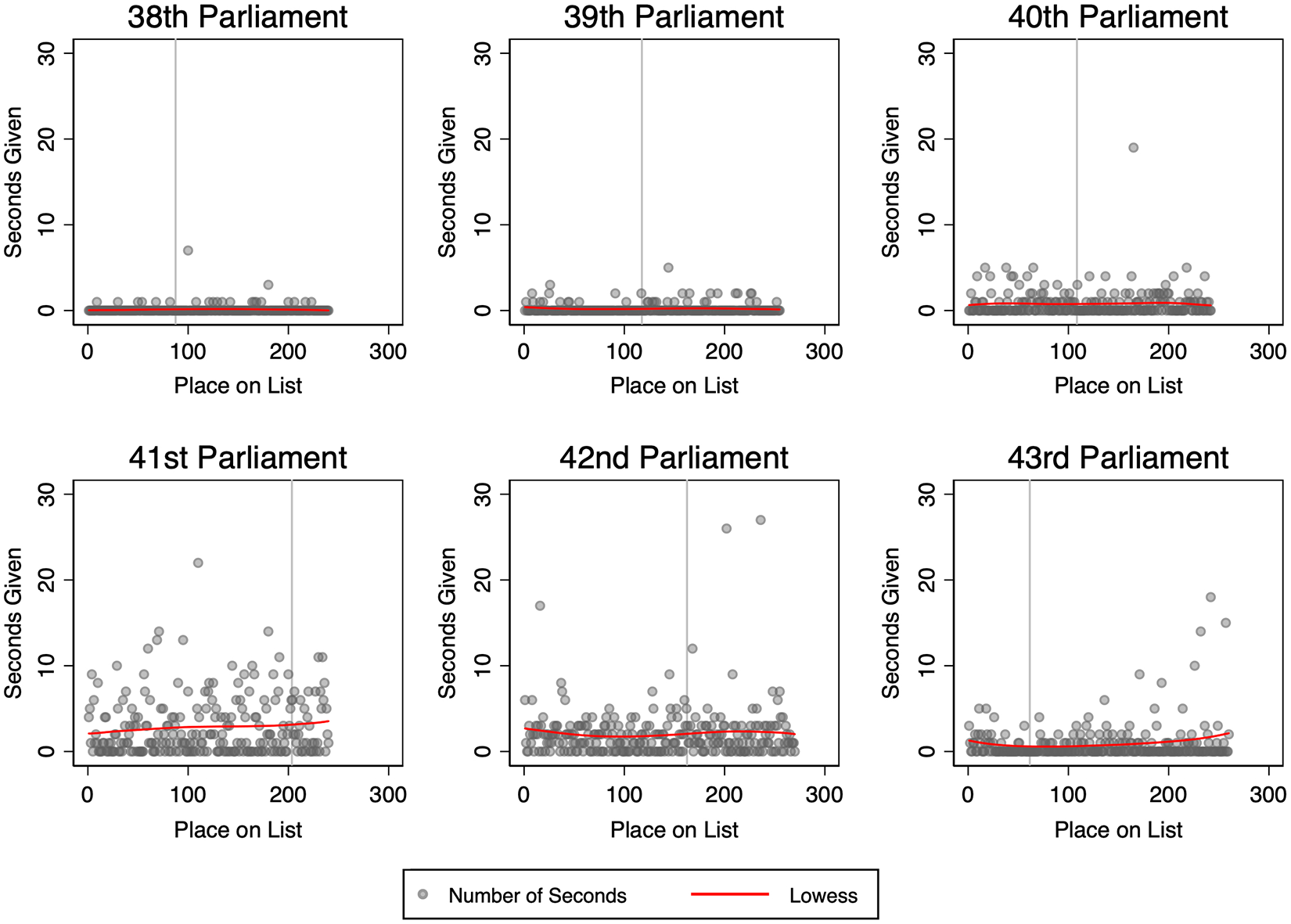
Figure 2. Relationship Between Number of Seconds Given and Place on List.
How does the lottery affect the number of seconds that MPs receive? For each parliament, Figure 3 illustrates the relationship between the number of seconds received and an MP’s place on the list. This figure focuses primarily on MPs with numbers low enough to enable them to make a proposal. As indicated earlier, seconders can be added when a bill has been introduced, until the debate starts at the second reading. Not all proposals reach the second reading; members whose lottery numbers fall short of this threshold automatically receive zero seconds in the analyses.
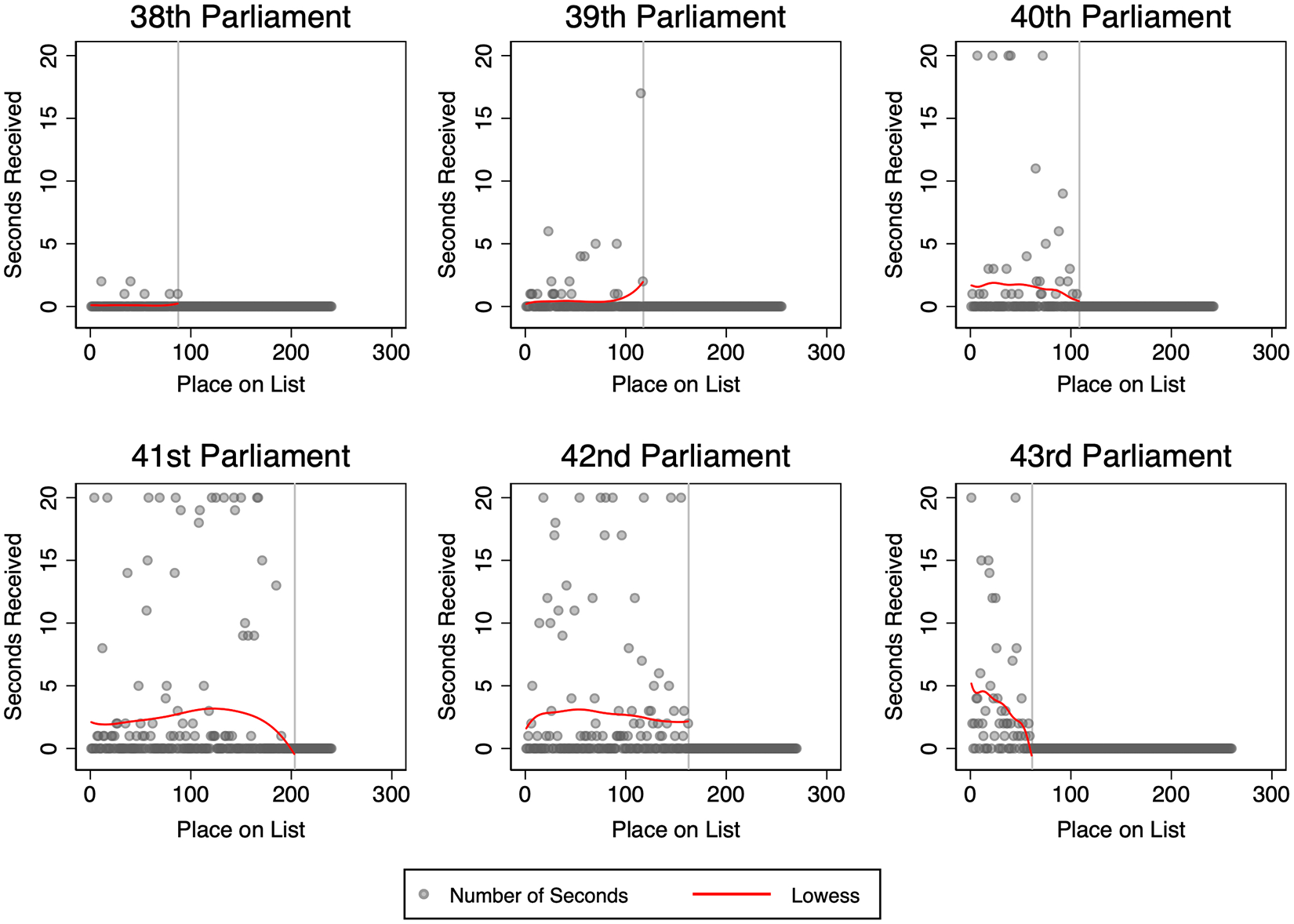
Figure 3. Relationship Between Number of Seconds Received and Place on List.
The fitted LOESS line is estimated and graphed only for those members eligible to receive seconds. No consistent pattern emerges from these LOESS plots. In three of the parliaments under study, there appears to be a slight advantage among those with the best lottery numbers, but the pattern seems unclear when we look at all six sessions, and we must once again investigate more closely using statistical analysis.
Table 4 presents the results of fitting equations 1-6 to our data. Model 1 shows that there is little, if any, relationship between an MP’s priority number and a binary indicator of whether an MP seconds a proposal during a session. However, Model 3 shows a positive significant relationship between place on the list and the number of seconds an MP gives during a session, implying that MPs with worse priority numbers tend to give more seconds. Since place on list is rescaled here to be between 0 and 1 (where 0 represents the first priority number on the list and 1 represents the last), a coefficient of 0.413 implies that the expected difference in the number of seconds given by the first member on the list and the last member on the list is less than one-half, or about one-sixth of a standard deviation. The top of the 95% interval is 0.413 + (1.96)(0.195) = 0.80.Footnote 13 Model 4 shows no clear nonlinear relationship between place on the list and the number of seconds an MP gives.
Table 4. Regression estimates of the marginal effects of lottery number of seconds given and received
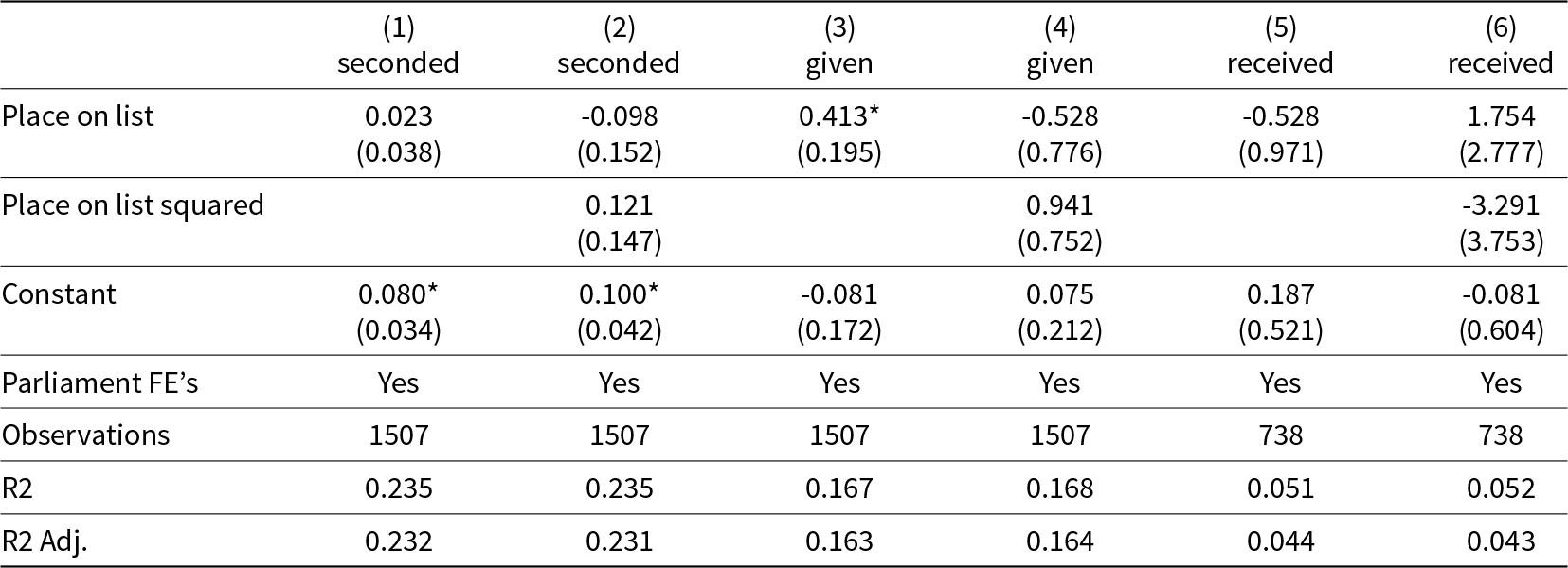
Standard errors in parentheses. Place on list varies from 0 to 1, with 0 representing the highest priority number in each parliament. Estimates in columns (5) and (6) are based on MPs whose lottery numbers were low enough to enable them to make proposals.
*![]() $p \lt 0.05$.
$p \lt 0.05$.
Model 5 shows a weak and statistically insignificant linear relationship between place on list and the number of seconds an MP receives. Bear in mind that these regressions are restricted to MPs who have the power to propose. (Had we included the full range of lottery numbers, the place on list regressor would have been significant simply because the number of seconds is automatically zero for MPs whose proposals never made it to second reading. See Table B.3. Nor do we find evidence of a curvilinear effect of the place on list on any of our dependent variables. Contrary to the intuition that those with the most favorably priority numbers would lack the time necessary to find seconders for their proposals, we do not find evidence that MPs with middling priority numbers are especially likely to attract or give/trade seconds. Although it is mechanically true that lottery “winners” receive more seconds than lottery “losers,” when we focus solely on winners, their relative priority seems to bear little apparent relationship to the number of seconds they garner.
In order to improve the precision with which the causal effect of lottery number is estimated, Table B.2 includes as a covariate the number of seconds that an MP made in the previous session. If a given MP was not in the previous session of parliament, this variable is assigned a value of 99; our regression model includes the binary variable Missing t − 1, which indicates whether a given MP was missing in the previous parliament. The results are similar.Footnote 14 We continue to see no evidence of nonlinear effects. The apparent linear effect of lottery numbers on seconds given, which was equivocal in Table 4; is even more so now. Our best guess is that those with unfavorable lottery numbers are somewhat more likely to second others’ proposals, but the magnitude of the effect is statistically ambiguous. Similarly, among MPs whose lottery number enabled them to make a proposal, we again see little indication that MPs with especially favorable (or unfavorable) lottery numbers attract more seconds in the current parliament.
7. Reciprocity across parliaments?
The lottery system also sets the stage for a test of reciprocity across parliaments. In a given parliament, some legislators will by chance have the power to offer a proposal, which in turn means that they will be in a position to accept seconds from other legislators. Thus, an MP’s favorable lottery number may cause that legislator to owe favors to others who support the proposal by seconding it. For concreteness, let’s call the legislator in the current parliament A and call the legislator with a favorable lottery number in the next parliament B. Because B can make proposals in the next parliament, legislator A may decide to second B’s proposal. The hypothesis is that A should be more likely to do so if given the power to propose in the current parliament.
Of course, which specific legislators decide to second a particular proposal depends on unobservables, such as shared party or ideology. The identification strategy here amounts to an encouragement design whereby some legislators in the current parliament are randomly assigned to receive favors (by virtue of being able to make proposals); some legislators of type A go on to receive seconds, but many do not. Those who would receive seconds if assigned a favorable lottery number may be characterized as “compliers,” using the familiar terminology by Angrist et al. Reference Angrist, Imbens and Rubin(1996). Those who would not receive seconds if assigned a favorable lottery number may be characterized as “never-takers.” This design allows us to estimate two causal quantities of interest. The first is the intent-to-treat effect of assignment to a favorable lottery number in the current parliament on seconding in the next parliament. The attractive feature of this approach is that it provides a direct test of the null hypothesis of no effect based on a simple regression. The dependent variable is whether legislators of type B who have the power to propose in the next parliament receive a second from legislators in the current parliament. The independent variable is a binary indicator of whether legislators in the current parliament won the power to offer a proposal (and hence to receive seconds). Note that for purposes of selecting relevant dyads, this regression excludes those who have unfavorable lottery numbers in the next parliament (because they cannot receive seconds) and excludes those who were not eligible for the lottery in the current parliament. These exclusions imply that we restrict attention to the five most recent parliaments, because the first parliament had no previous lottery.
Another quantity of interest is the average causal effect among compliers. Obtaining consistent estimates of this quantity requires an additional assumption, excludability, which holds that the lottery has no effect on seconding B’s proposal except insofar as it increases A’s chance of receiving a second. This analysis is also subject to a good deal of statistical uncertainty because compliers are relatively rare (i.e., few lottery winners receive seconds). For this reason, we focus our attention on the intent-to-treat effect. From the standpoint of hypothesis testing, the estimated intent-to-treat effect is arguably the proper test statistic and the mechanics of conducting a hypothesis test are much simpler (Chernozhukov and Hansen, Reference Chernozhukov and Hansen2008).
Table 5 reports the estimates from the intent-to-treat regression for each parliament and for all parliaments pooled. We use dyadic cluster-robust standard errors as described by Aronow et al. Reference Aronow, Samii and Assenova(2015). The effect of having an opportunity to propose on subsequent seconding is weakly positive in four of the five sessions, hinting that some legislators who win the power to propose may be induced to return favors. However, even when pooling all of the sessions, this effect is not clearly distinguishable from zero. Assignment to the power to propose in a given parliament elevates the probability of offering a second in the next parliament by 0.13 percentage points with a standard error of 0.12 percentage points. The 95 percent confidence interval ranges from -0.11 to 0.36 percentage points.Footnote 15
Table 5. Effects of power to propose in previous parliament on directed dyadic support, by parliament
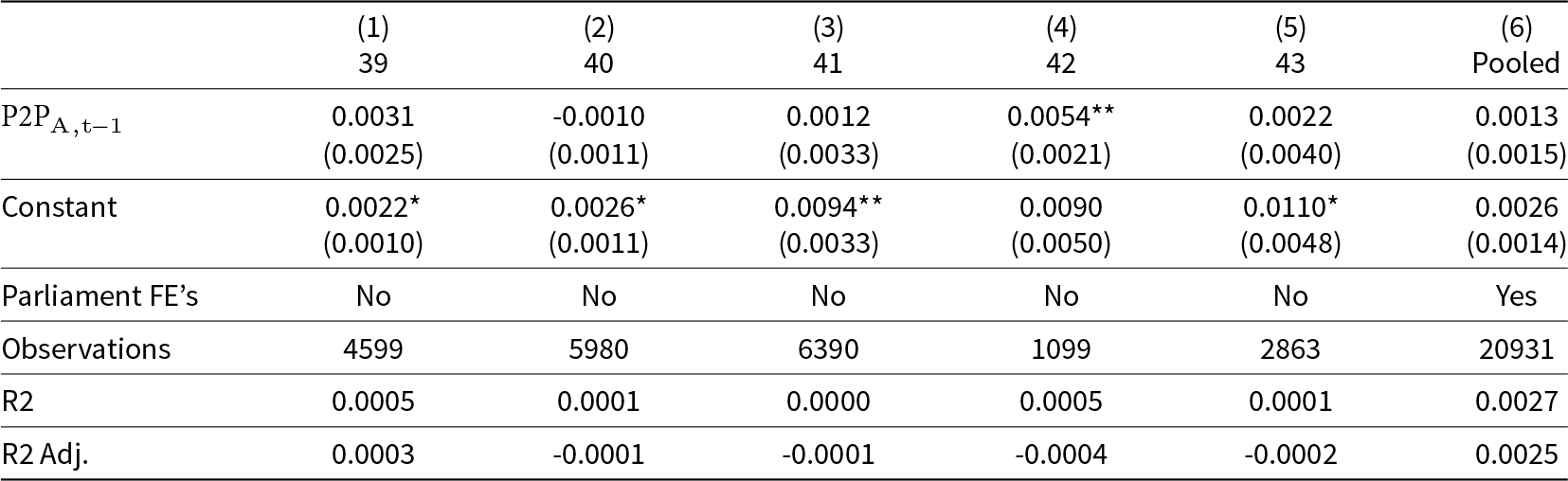
Dyadic cluster robust standard errors in parentheses *![]() $p \lt 0.05$, **
$p \lt 0.05$, **![]() $p \lt 0.01$.
$p \lt 0.01$.
In sum, the intent-to-treat point estimate hints that winning the proposal lottery sets in motion subsequent seconding, but we cannot rule out the null hypothesis that the intent-to-treat effect is zero. Delving more deeply into the encouragement design, we note that of the 333 MPs who were eligible to offer proposals in the current period and also had an opportunity to second another eligible MPs proposal in the next period, 22 are compliers (i.e., they received seconds in the current period and were therefore in a position to reciprocate). Because winners in the current lottery are a random sample of eligible MPs, we infer that 6.61 percent of the MP subject pool are compliers. To estimate the complier average causal effect, we divide the intent-to-treat effect by 0.0661, or multiply by 15.1. Interestingly, even this inflation factor produces an estimate of (15.1)(0.0013) = 0.02. This two percentage point rise in the probability of seconding in the next parliament is substantively small.
A closer look at seconding sequences in these five parliaments underscores the meager empirical evidence for reciprocity. Just six MPs whose proposals received a second went on to second one of the seconder’s proposals in the next parliament. All six of these dyads were from the same party. This fact does not necessarily rule out the influence of reciprocity but does illustrate that even observational evidence of reciprocity is limited in this context, and the pattern we observe could be attributed to homophily given that every instance occurs between co-partisans.
8. Conclusion
Although much has been written on “back-scratching” in legislatures, the literature largely consists of enticing narratives and correlations. The narratives illustrate instances in which legislators were able to strike bargains, and the correlations demonstrate that legislators with similar attributes are especially likely to second in mutually supportive ways. Still, the question remains: do apparent instances of reciprocity reflect a causal effect whereby one legislator’s behavior changes in response to another legislator’s actions, or do they reflect the operation of some unmeasured shared characteristic that led both legislators to support the same bill?
To our knowledge, the current study is the first to leverage random assignment in order to study legislative reciprocity in a naturalistic setting. Taking advantage of the random endowment of proposal power in the Canadian House of Commons, we examine the conditions under which MPs give or attract seconds. Perhaps surprisingly, we find no clear pattern of exchange resulting from this random endowment of proposal power. Those with favorable lottery numbers are not especially enterprising about attracting seconds, nor do they offer more seconds in an apparent effort to attract more seconds in return. The same may be said of legislators with middling lottery numbers; they have more time to garner seconds but seem no more likely to give or receive them.
When we look at patterns of seconding over time, we find tepid support for the hypothesis that lottery-induced seconds received in one parliament lead MPs to return the favor in the next parliament. The point estimate is weakly positive, and so we cannot rule out a possible reciprocity effect. However, the confidence interval brackets zero, which implies that further investigations of this sort using future parliaments may well converge on estimates that are too small to be substantively meaningful. At a purely descriptive level, the stubborn fact is that pooling data from several parliaments, we find only six instances in which a proposer who attracted a second in one parliament returned the favor when the seconder became a proposer in the ensuing parliament. Lottery-induced reciprocity seems rare, even when we restrict attention to MPs from the same party.
Our data include six MPs across two parliaments who received at least two seconds (but no more than 20) in the current parliament and provided at least two seconds in both the current and previous parliaments. One MP has passed away, and another is no longer in politics. We contacted the remaining four MPs, who are still active in Parliament: two from the Conservative Party, one from the NDP, and one from the Liberal Party. Three MPs began working on their bills only after learning their position in the lottery, and one mentioned that work started earlier because their issue had carried over from a previous Parliament. None of the MPs indicated they seconded bills to receive reciprocal support for their own proposals. They emphasized that seconding was done based on the bill’s merit or relevance to their riding, not as a trade for future support.Footnote 16
One possible explanation for the pattern of findings both within and across parliaments is that Canadian legislators are unaccustomed to exchanging seconds, given the strong party discipline in floor votes. In that sense, the weak causal effect observed here reflects the character of party politics in this setting. Elsewhere, we might observe stronger evidence of reciprocity—a good reason to extend the study of seconding to other countries that have a lottery-driven system of PMB. Another possibility is that seconds themselves are sincere rather than strategic expressions of support, and those with the poorest lottery numbers offer them up because, lacking an opportunity to offer a proposal, they have no legislative avenue through which to express their own views. Sincere seconding might explain both the lack of reciprocity we see here and the strong correlation between seconding behavior in other countries, where like-minded legislators have ample opportunity to express their shared preferences via seconding.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/psrm.2025.10032. To obtain replication material for this article, https://doi.org/10.7910/DVN/K143VW.
Acknowledgements
We thank the Hon. Tony Clement, PC, Hon. Nathaniel Erskine-Smith, PC, David Fortunato, John Griffin, Jean-François Godbout, Michael Kistner, Mr. Alistair MacGregor, Can Mekik, Hon. Thomas Mulcair, PC, Hon. Bob Rae, PC, Robert Schertzer, Adam Zelizer, Office of the Private Members’ Business of the House of Commons, seminar participants at the 2023 Canadian Political Science Association, the 2023 Midwest Political Science Association, and the anonymous reviewers and MPs for helpful comments. Author names are listed in alphabetical order.









